AUC定义
用途:用来度量分类模型好坏的一个标准 背景: - 有些时候,仅仅依靠正确率是不妥当的。 - 能客观反映对正样本、负样本综合预测的能力,还要考虑消除样本倾斜的影响。
ROC
- ROC:Receiver Operating Characteristic
- ROC曲线:横坐标是false positive rate(FPR),纵坐标是true positive rate(TPR)。
- 对某个分类器而言,我们可以根据其在测试样本上的表现得到一个TPR和FPR点对。这样,此分类器就可以映射成ROC平面上的一个点。
- 调整这个分类器分类时候使用的阈值,我们就可以得到一个经过(0, 0),(1, 1)的曲线,这就是此分类器的ROC曲线。
tip:FPR和TPR 先来看一个普遍的二分类问题的结果,预测值和实际值有4种组合情况,看下面的表格: 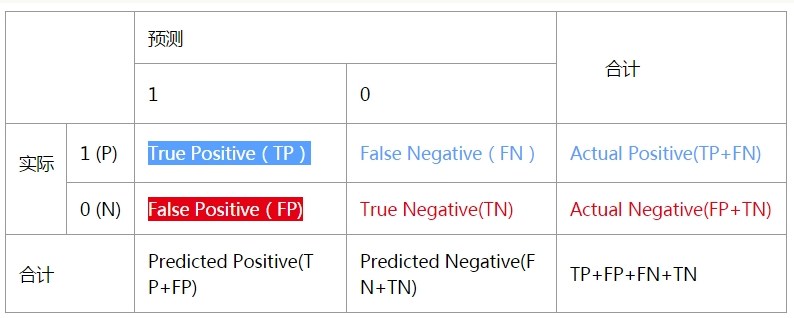 我们定义 \[ TruePositiveRate(TPR) = \frac{TP}{TP+FN=P} = \frac{正确预测1}{正确预测1+错误预测1=1的数量}=实际正样本正确预测的比例\] \[ FalsePositiveRate(FPR) = \frac{FP}{FP+TN=N} = \frac{错误预测0}{错误预测0+正确预测0=0的数量}=实际负样本错误预测的比例\]
我们定义 \[ TruePositiveRate(TPR) = \frac{TP}{TP+FN=P} = \frac{正确预测1}{正确预测1+错误预测1=1的数量}=实际正样本正确预测的比例\] \[ FalsePositiveRate(FPR) = \frac{FP}{FP+TN=N} = \frac{错误预测0}{错误预测0+正确预测0=0的数量}=实际负样本错误预测的比例\]
如何一个分类器的画ROC曲线
概率输出:即表示分类器认为某个样本具有多大的概率属于正样本(或负样本),来动态调整一个样本是否属于正负样本 例: - 图中共有20个测试样本 - “Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本) - “Score”表示每个测试样本属于正样本的概率。 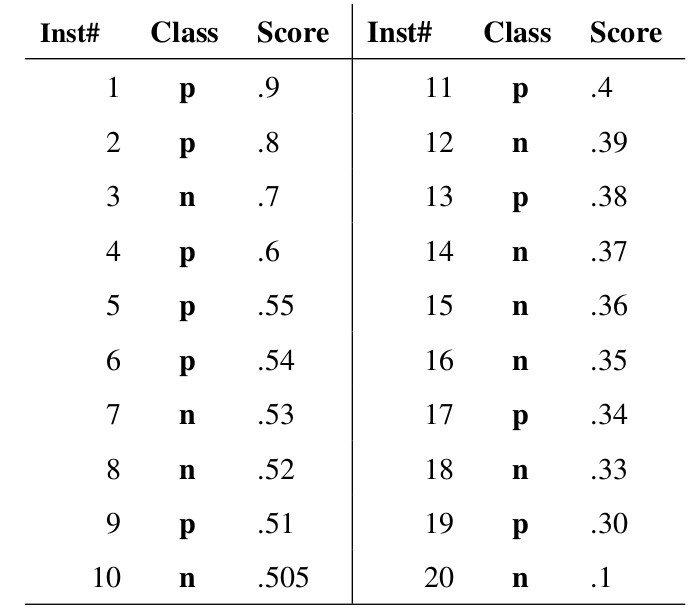 步骤: - 从高到低,依次将“Score”值作为阈值,当测试样本属于正样本的概率大于或等于这个阈值时,我们认为它为正样本,否则为负样本。 - 举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。 - 每次选取一个不同的阈值,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
步骤: - 从高到低,依次将“Score”值作为阈值,当测试样本属于正样本的概率大于或等于这个阈值时,我们认为它为正样本,否则为负样本。 - 举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。 - 每次选取一个不同的阈值,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图: 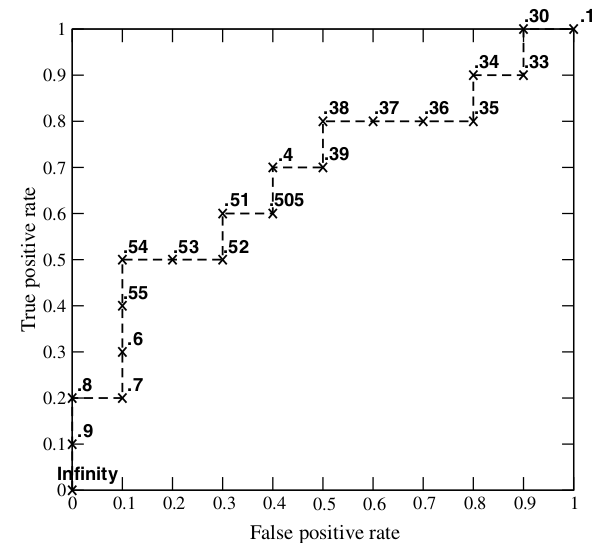 - 当我们将阈值设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。 - 当阈值取值越多,ROC曲线越平滑。
- 当我们将阈值设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。 - 当阈值取值越多,ROC曲线越平滑。
AUC
- AUC的值就是处于ROC curve下方的那部分面积的大小
- 通常,AUC的值介于0.5到1.0之间
- 较大的AUC代表了较好的performance
计算AUC的方法
- 直接计算AUC是很麻烦的,所以就使用了AUC的一个性质(它和Wilcoxon-Mann-Witney Test是等价的)来进行计算。
- Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本,正类样本的score有多大的概率大于负类样本的score。
- 有了这个定义,我们就得到了另外一中计算AUC的办法:得到这个概率。
方法一
统计一下所有的 M×N(M为正类样本的数目,N为负类样本的数目)个正负样本对中,有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候,按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数(即n=M+N)。 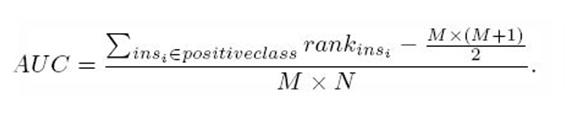
方法二
第二种方法实际上和上述方法是一样的,但是复杂度减小了。
- 首先对score从大到小排序
- 然后令最大score对应的sample 的rank为n,第二大score对应sample的rank为n-1,以此类推
- 然后把所有的正类样本的rank相加,再减去正类样本的score为最小的那M个值的情况。
- 得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。
- 然后再除以M×N。即
AUC=((所有的正例位置相加)-M*(M+1))/(M*N)
另外,特别需要注意的是,再存在score相等的情况时,对相等score的样本,需要 赋予相同的rank(无论这个相等的score是出现在同类样本还是不同类的样本之间,都需要这样处理)。具体操作就是再把所有这些score相等的样本 的rank取平均。然后再使用上述公式。