在说LR之前,我们先回顾一下logistic分布。
logistic分布
如果连续随机变量\(X\)服从logistic分布,则\(X\)具有下列分布函数和密度函数:
\[ F(x)=P(X<=x)=\frac{1}{1+e^{-(x-u)/r}} \]
\[ f(x)=F'(x)=\frac{e^{-(x-u)/r}}{r(1+e^{-(x-u)/r})^2} \]
其中
\(u\)为位置参数
\(r>0\)为形状参数
其中,密度函数与分布函数的形状如图所示 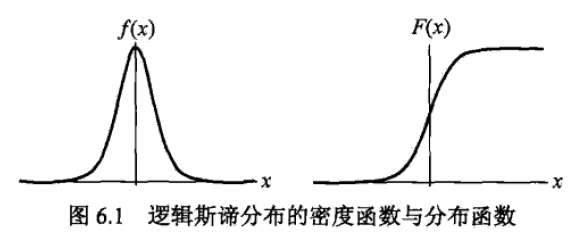
备注:分布密度函数与分布函数
概率密度函数\(f(x)\):表示瞬时值落在某区间的概率,是幅值的概率。++用来描述连续型随机变量取值的密集程度的。++\(f(x)\)表示X=x的概率是\(\int_0^1f(x)\)。
\(P(X=x|x \in (0,1))=\int_0^1f(x)\)
分布函数\(F(x)\):描述随机变量落在任一区间的概率。
\(F(x)=P(X<=x)\)
关系:
分布函数\(F(x)\)是概率密度函数\(f(x)\)从负无穷到正无穷上的积分;
在坐标轴上,概率密度函数的函数值y表示落在x点上的概率为y;分布函数的函数值y则表示x落在区间(-∞上的概率。
二项logistic回归模型
用途:估计某个值的为哪一类的概率
logistic回归是分类问题。前面我们讲的分类问题的输出都是 “yes”或者“no”。但是在现实生活中,我们并不是总是希望结果那么肯定,而是概率(发生的可能性)。比如,我们希望知道这个房子在第三个星期被卖出去的概率。那么以前的分类算法就无法使用了,这时logistic 回归就派上了用场。
定义
二项logistic回归模型是如下的条件概率分布:
\[ P(Y=1|x)=\frac{exp(wx+b)}{1+exp(wx+b)} \]
\[ P(Y=0|x)=\frac{1}{1+exp(wx+b)} \]
其中: \(x \in R^n\) :输入
\(Y \in (0,1)\) :输出
给定\(x\),可以求得\(P(Y=1|x)\)和\(P(Y=0|x)\)
logistic回归模型的特点
几率(odds)= 该事件发生的概率/该事件不该发生的概率,则对数几率:
\[ log(odds)=log(\frac{p}{1-p})=log(\frac{P(Y=1|x)}{1-P(Y=1|x)})=wx \]
则:输出Y=1的对数几率=输入x的线性函数
模型参数估计
输入: 一堆(x,y)
目标:估计参数w,b
方法:极大似然法

总结
- 逻辑回归是一种预测y的各类别的概率的模型,即计算P(Y=1|x)或者P(Y=0|x)
- 与机器学习过程类似,即 通过已知的大量(x,y),拟合计算参数w,b;再用y=wx+b来计算新的x下的y;把y输入sigmoid函数中,得到y为1的概率。
LR推导(sigmoid,损失函数,梯度,参数更新公式)
这篇文章非常详细地介绍了逻辑回归的推导。非常有用。我在此处进行了转载。
声明
- $ x(1),x(2),...,x(m) $ 表示 n 维空间的一个样本,\(x(i)\) 表示第i个样本,\(x(i)_j\) 表示第i个样本的第j维的数据(因为\(x\)是一个n维向量)。
- \(y(1),y(2),...,y(m)\) 表示 k 维空间的一个观测结果,记k从1,2,...,k变化,即分类问题中的k个类别,也可以0为下标开始,不影响推导。
- \(\pi()\)是我们学习到的概率函数,实现样本数据到预测结果的映射:\(R^n\rightarrow R^k\),(其实就是样本经过函数 \(\pi()\)计算后得到各个类别的预测概率,即一个k维向量), \(\pi(x)_u\)表示数据样本x属于类别u的概率,我们希望\(\pi()\)具有如下性质:
- \(\pi(x)_v>0\) (样本x属于类别v的概率大于0,显然概率必须大于0)
- \(\sum_{v=1}^k\pi(x)_v = 1\),样本x属于各个类别的概率和为1
- \(\pi(x(i))_{y(i)}在所有类别概率中最大\)
- \(A(u,v)\)是一个指示函数,\(当u=v时A(u,v)=1,当u\neq v时A(u,v)=0,如A(u,y(i))\)表示第i个观测结果是否为u
逻辑回归求解分类问题过程
对于二分类问题有k=2,对线性回归函数\(\lambda x\)进行非线性映射得到:
\[ \pi(x)_1 = \frac{\rm e^{\lambda \cdot x}}{\rm e^{\lambda \cdot x}+1}\tag{1} \] \[ \pi(x)_2 = 1-\pi(x)_1= \frac{1}{\rm e^{\lambda \cdot x}+1}\tag{2} \] 对于多分类问题有: \[ \pi(x) = \frac{\rm e^{\lambda _v\cdot x}}{\sum_{u=1}^m\rm e^{\lambda_u \cdot x}}\tag{3} \] 对\(\lambda\)求偏导可得:
\[ \begin{aligned} u = v 时, \frac {\partial\,\pi (x)_v}{\lambda_{v,j}} &= \frac{x_j\rm e^{\lambda _{v,j}\cdot x}\cdot \sum_{u=1}^m\rm e^{\lambda_{u,j} \cdot x}-x_j\rm e^{\lambda _{v,j}\cdot x}\rm e^{\lambda _{v,j}\cdot x}}{(\sum_{u=1}^m\rm e^{\lambda_{u,j} \cdot x})^2}\\ & = \frac{x_j\rm e^{\lambda _{v,j}\cdot x}}{\sum_{u=1}^m\rm e^{\lambda_{u,j} \cdot x}} \cdot \frac{\sum_{u=1}^m\rm e^{\lambda_{u,j} \cdot x}-\rm e^{\lambda_{v,j}\cdot x}}{\sum_{u=1}^m\rm e^{\lambda_{u,j} \cdot x}}\\& = x_j \pi(x)_v(1-\pi(x)_v)\end{aligned}\tag{4} \]
\[ \begin{aligned} u \neq v 时 \frac {\partial\,\pi (x)_v}{\lambda_{u,j}}&=-\frac{\rm e^{\lambda_{v,j} \cdot x} \cdot (x_j\rm e^{\lambda_{u,j} \cdot x})}{(\sum_{u=1}^m\rm e^{\lambda_{u,j} \cdot x})^2} \\ &= -x_j \pi(x)_v\pi(x)_u, u\neq v时 \end{aligned} \tag{5} \] 该分类问题的最大似然函数为: \[ L(\lambda)=\prod_{i=1}^m \pi(x(i))_{y(i)}\tag{6} \] 取对数得: \[ f(\lambda)=\log L(\lambda)=\sum_{i=1}^m \log(\pi(x(i))_{y(i)})\tag{7} \] 求似然函数最大值,令: \[ \begin{aligned} \frac{\partial\,f(\lambda)}{\partial \,\lambda_{u,j}} &=\frac{\partial}{\partial \,\lambda_{u,j}}\sum_{i=1}^m \log(\pi(x(i))_{y(i)}) \\ &= \sum_{i=1}^m \frac{1}{\pi(x(i))_{y(i)}}\frac{\partial}{\partial \,\lambda_{u,j}}\pi(x(i))_{y(i)} \\ &= \sum_{\begin{array}{c}i=1,\\y(i)=u\end{array}}^m \frac{1}{\pi(x(i))_{y(i)}}\frac{\partial}{\partial \,\lambda_{u,j}}\pi(x(i))_{u} + \sum_{\begin{array}{c}i=1,\\y(i)\neq u\end{array}}^m \frac{1}{\pi(x(i))_{y(i)}}\frac{\partial}{\partial \,\lambda_{u,j}}\pi(x(i))_{y(i)}\\ &= \sum_{\begin{array}{c}i=1,\\y(i)=u\end{array}}^m \frac{1}{\pi(x(i))_{y(i)}}x(i)_j\pi(x(i))_u(1-\pi(x(i))_u) \\ &\quad - \sum_{\begin{array}{c}i=1,\\y(i)\neq u\end{array}}^m \frac{1}{\pi(x(i))_{y(i)}}x(i)_j\pi(x(i))_{y(i)} \pi(x(i))_u\\ &= \sum_{\begin{array}{c}i=1,\\y(i)=u\end{array}}^m x(i)_j(1-\pi(x(i))_u)-\sum_{\begin{array}{c}i=1,\\y(i)\neq u\end{array}}^m x(i)_j \pi(x(i))_u \\ &= \sum_{\begin{array}{c}i=1,\\y(i)=u\end{array}}^m x(i)_j - \sum_{i=1}^m x(i)_j\pi(x(i))_u \\ &= 0 \end{aligned} \tag{8} \] 得: \[ \sum_{\begin{array}{c}i=1,\\y(i)=u\end{array}}^m x(i)_j = \sum_{i=1}^m x(i)_j\pi(x(i))_u\tag{9} \] 代入\(A(u,y(i))=1\)得: \[ \sum_{i=1}^m x(i)_j\pi(x(i))_u = \sum_{i=1}^m x(i)_jA(u,y(i))\tag{10} \] 综上有: \[ \frac{\partial\,f(\lambda)}{\partial \,\lambda_{u,j}}=\sum_{i=1}^m x(i)_j(A(u,y(i))-\pi(x(i))_u)\tag{11} \] 则参数更新公式为:
\[ \begin{aligned}\lambda_{u,j} &= \lambda_{u,j} - \alpha \cdot \frac{\partial\,f(\lambda)}{\partial \,\lambda_{u,j}} \\&= \lambda_{u,j} - \alpha \cdot \sum_{i=1}^m x(i)_j(A(u,y(i))-\pi(x(i))_u)\end{aligned}\tag{12} \]
sigmoid函数的由来(最大熵)
由上文已知\(\pi()\)具应有如下性质:
- 样本x属于类别v的概率大于0,显然概率必须大于0\(\pi(x)_v>0\tag{13}\)
- 样本x属于各个类别的概率和为1 \(\sum_{v=1}^k\pi(x)_v = 1\tag{14}\)
- \(\pi(x(i))_{y(i)}在所有类别概率中最大\)
其中对最后一个条件等价于尽可能的让\(\pi(x(i))\rightarrow y(i)\) 即 \(\pi(x(i))\rightarrow A(u,y(i))\),理想情况为\(\pi(x(i))= A(u,y(i))\)固有: \[ \sum_{i=1}^m x(i)_j\pi(x(i))_u = \sum_{i=1}^m x(i)_jA(u,y(i))\tag{15},对所有的u,j都成立 \]
对所有类别及所有样本取\(\pi()\)的熵,得: \[ f(v,i)=-\sum_{v=1}^k\sum_{i=1}^m\pi(x(i))_v \log(\pi(x(i))_v)\tag{16} \] 得到一个优化问题:
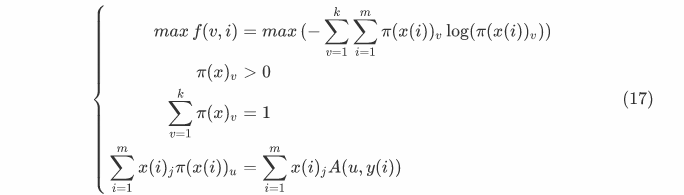
\[\left\{ \begin{aligned} max f(v,i)=max (-\sum_{v=1}^k \sum_{i=1}^m pi(x(i))_v log(π(x(i))_v))\\ \pi(x)_v>0\\ \sum_{v=1}^k π(x)_v = 1\\ \sum_{i=1}^m x(i)_j π(x(i))_u = \sum_{i=1}^m x(i)_j A(u,y(i)) \end{aligned} \right. \tag{17}\] 利用拉格朗日对偶性求这个优化问题的对偶问题,首先引入拉格朗日函数:
\[ \begin{aligned}L &= \sum_{j=1}^n\sum_{v=1}^k\lambda_{v,j} \left( \sum_{i=1}^m\pi(x(i))_vx(i)_j-A(v,y(i))x(i)_j \right)\\&+ \sum_{v=1}^k\sum_{i=1}^m\beta_i(\pi(x(i))_v-1)\\&- \sum_{v=1}^k\sum_{i=1}^m\pi(x(i))_v\log(\pi(x(i))_v)\end{aligned}\tag{18} \] 其中 \[ \beta<0 \] ,由KKT条件有: \[ \frac{\partial\,L}{\partial \,\pi(x(i))_u} = \lambda_u\cdot x(i)+\beta_i-\log(\pi(x(i))_u) - 1 = 0 \quad对所有i,u \tag{19}\]
\[则:\pi(x(i))_u = e^{\lambda_u \cdot x(i)+\beta_i-1} \tag{20}\]
则: \[\pi(x(i))_u = e^{\lambda_u \cdot x(i)+\beta_i-1} \tag{20}\] 由(14)式得到: \[ \sum_{v=1}^k e^{\lambda_u \cdot x(i)+\beta_i-1} = 1\\ \] 即: \[e^\beta=\frac{1}{\sum_{v=1}^ke^{\lambda_u \cdot x(i)-1}} \tag{21} \] 代入(21)式消去常数项得: \[ \pi(x(i))_u=\frac{e^{\lambda_u \cdot x}}{\sum_{v=1}^ke^{\lambda_u \cdot x}}\tag{22} \] 即多分类问题对应的sigmoid函数