决策树简介
模仿人类决策的过程

- 优点:好理解;简单
- 缺点:缺少很强的理论支持;树结构不唯一;
决策树的表达方式
如上图所示的决策树,我们用\(G(x)\)来表达决策树:
\[G(x)=\sum_{t=1}^T q_t(x)\cdot g_t(x) \]
tips:
- \(g(x)\)是最终的决策(
Y or N),叶子节点 - \(q_t(x)\)是条件,
condition。就是橘色箭头的判断过程 - 内部的决策过程,例如
deadline?,内部节点
那么决策树的表达就有两种方式:
路径角度。将每个从根到叶子的路径作为一个假设g,通过不同的条件组合得到最后的G(X)。
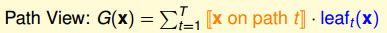
递归角度。父树是由子树递归定义的
tree=(root,sub-trees)
基本流程
- 如何分支(branching criteria),即如何得到\(b(x)\)
- 根据分支,数据如何分块
- 根据数据,如何学习子树
- 得到最终的决策树

CART算法
- Classification And Regression Tree,分类回归树
- 二叉树(只有是、否)
- 输入:随机变量\(X\)
- 输出:随机变量\(Y\)的条件概率分布
- \(g_t(x)\)返回一个常数(根据不同的条件,对数据进行切分,到达叶子节点时,根据剩下的数据进行预测,输出一个常数)
纯度
纯度的定义
- CART算法中每个节点(看做是一个决策桩decision stump)对数据进行切分,如果分出来的数据的y都很接近(回归问题)或者都一样(分类问题),那么我们说这样的数据是“纯的”,这样用标量对数据进行预测可以得到比较小的误差。
CART分支\(b(x)\)为: 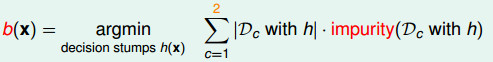
- 我们通过上面的公式,来计算对于每一个节点的决策桩来说,分出来的两份数据的纯度是怎样的。
- 该公式通过计算数据集
Di(i=1 or 2)的纯度并根据数据集的数量对其进行加权 - 其加权的意义是如果数据集的数量比较大的话,那个纯度对其比较重要
- 反之,就不那么重要。
- CART通过分出的两部分数据综合起来的纯度对决策桩进行选择,选择“最纯”的分割方式作为当前的分支。
纯度的计算函数
我们可以将分割出来的数据和回传的常数的误差作为评价纯度的方法,利用数据的y和回传的y_ba的均方误差来评价回归问题的纯度;利用0/1误差函数来评价分类问题的纯度。

如果是分类问题,我们还可以使用一个别的方法。通过基尼不纯度来度量分类问题的纯度问题。

终止条件
CART中有两种被迫终止的情况,分别是:
yn都一样,这时不纯度为0,于是可以得到gt(x)=yn;xn都一样,就没有继续分割的可能了。- CART树长到被迫停下来的情况,称为完全长成的树(fully-grown tree)。
下面是CART算法完整流程:

CART剪枝
预防过拟合

上图告诉我们使用叶子的数目作为正则项(regularizer),最终得到一个正则化的决策树。 关于剪枝的具体做法时:
- 首先得到完全长成的树作为
G(0); - 然后试图摘掉一片叶子,将所有摘掉一片叶子后的树计算
Ein,将最小的那棵摘掉一片叶子的数作为G(1); - 如此这般,得到摘掉两片叶子的最优树
G(2),这样不断剪枝,直到根结点,形成一个子树序列; - 最终对这个子树序列使用
argmin Ein(G)+λΩ(G)来得到最后的输出。
参考资料
- Jason Ding,决策树算法
- 机器学习技法课程,林轩田,台湾大学