引言
回顾之前学习过的两个算法:
- Bagging -- 简要:通过bootstrapping得到不一样的数据,得到不同的g,对g取平均得到G -- 特点:通过投票和平均的方式来降低对不同数据的敏感性(variance的效果)
- 决策树 -- 简要:通过递归方式建立子树,最终得到完整的树 -- 特点:对不同数据较敏感(算法的variance很大)
- 随机森林 -- 两者的结合
随机森林算法
概述:利用随机的方式将许多决策树组合成一个森林,每个决策树\(g_t(t)\)在分类的时候投票决定测试样本的最终类别。在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一类被选择最多,就预测这个样本为那一类。
详细算法: 
左边的总算法是Bagging思想--体现随机性
其中为每个\(g_t(t)\)建树时,是决策树的思想--体现森林
并行计算的可能性:随机森林算法从Bagging过程中可以分配到不同的计算机中进行计算,每台计算机可以独立学习一棵树,不同的树之间没有任何依赖关系。这使得Bagging过程很容易实现并行化。
特征投影(Feature Project)
原来在Bagging中,我们对数据进行抽取,得到不同的数据集,从而产生不同的\(g_t\)
在随机森林算法中,除了对数据抽取,也可以在特征这一角度抽取
例,如果事先我们有100个特征,现在我们可以抽取10个特征
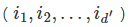
得到数据集

来训练一棵树,这样的方式我们也可以得到很不一样的树,其对于分类的标准显然也很不一样
这等效于一个特征转换,这个过程中,从100维度到10个维度的转换中,相当于作了低维度的投影(Projection)
一般来说,
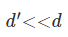
得到的特征实际上是原始特征的随机子集,这使得生成模型过程中的效率也大大提高了

特征扩展(feature Expansion)
每次随机抽取子空间 等效于 对原来的特征向量左乘一个投影矩阵\(P\),使得\(\Phi(X)=P\cdot x\)
更加有能力的特征投影就是不再单一选取单一维度的特征,而是将多个维度的特征进行组合(随机的方向),得到新的一维的特征,这称为特征扩展。

- 将多个方向的特征随机合起来(combination),即对于投影矩阵\(P\)的每一个方向\(p_i\),不再固定方向(row)。即变为\(\Phi_i(X)=P_i^T\cdot x\) -- 一般情况下,会考虑
low-dimensional,即投影过去时,一般每次选取少量维度进行投影。即只有\(d''\)的非零项被投影过去 - 这样的方式,包含了随机抽取(random subspace)的思想
- 一般来说,每次投影都采用新的不一样的投影
随机森林的采样过程
在建立森林的每颗决策树\(g_t\)的过程中,首先需要随机采样数据点。
不是所有数据点都能被采到。以下介绍OOB点
Out-of-bag(OOB)点
OOB点:在bootstrapping过程中,有些数据可能没有被选择,这些数据被称为OOB点。例如下表,对于训练每一个决策树\(g_t\),其中用*号标注的就是\(g_t\)的OOB 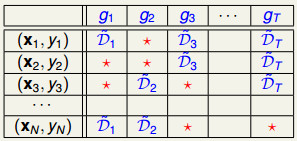
OOB点个数
假设bootstrapping抽了\(N'\)次数据,探讨会有多少数据不会被抽到: - 若\(N'=N\),某个数据\((x_n,y_n)\)从未被抽到的概率是\((1-\frac{1}{N})^N\) \[(1-\frac{1}{N})^N=\frac{1}{\frac{N}{N-1}^N}\approx \frac{1}{e}\] - 那么每个决策树\(g_t\)OOB集合的大小就约为\(\frac{1}{e}N\approx 0.3N\)
OOB用途-验证随机森林的G
可以用来做测试集-问题在于————验证g还是G? 以数据集\((x_N,y_N)为例\)
- 验证\(g\)的必要性不大
- 验证\(G\)不方便
- 可以用来验证
除了g1之外的G= \(G_N^-(x)=average(g_2,g_3,g_T)\) - 总之,用来验证\(G\)表现是否好的方式: \[E_{oob}(G)=\frac{1}{N}\sum_1^N error(y_n,G_n^-(x_n))\]
特征选择(feature selection)
目的:自动选择需要的特征,去除冗余、不相关的特征 优点:降维,减少复杂度;减少噪声,提高模型泛化能力;物理意义; 缺点:计算量大;可能导致过拟合;
下面介绍特征选择的方法。
根据重要性选择(线性的)
- 给每个特征算一个权重(分数)
- 问题:特征选择是线性的,不符合随机森林的非线性特点
置换检验(非线性的,Permutation Test)
问题:每个特征是有噪音的,由于噪音的存在,导致某些原本很优秀的特征的分数被降低
解决方法:将第i个维度特征的所有数据重新的随机调整位置,然后比较一下原始数据和调整之后的数据表现的差距,来评价这个维度的特征是有多么重要。
- 调整方法1:高斯什么的,但会改变数据原始分布
- 调整方法2:随机重排,即置换检验。将某一维度的数据随机重排,可以看出来这个维度有多重要。
在Out-Of-Bag Estimate过程中做Permutation Test
在随机森林中可以用OOB代替验证的过程,为了简化Permutation Test带来的重新进行训练的代价,我们在使用OOB Example(bootstrap过程中没有选取的数据)进行验证的过程中做一些修改,即在验证的时候去进行Permutation Test,而非训练时进行。 在求Eoob(G)时,我们通过G-(xn)来计算,我们在这里将x(n)修改成x(n,i),就可以不用对G进行修改了。  在实际应用中,面对非线性的问题时,可以通过随机森林的方法来进行初步的特征选择。
在实际应用中,面对非线性的问题时,可以通过随机森林的方法来进行初步的特征选择。

参考资料: 1. 机器学习的算法(1):决策树之随机森林 2. 机器学习技法