甲乙小朋友的房子

甲乙小朋友很笨，但甲乙小朋友不会放弃

0%

机器学习算法-AdaBoost

发表于 更新于 分类于

Boosting

提升（boosting）：从弱学习算法（正确率低）出发，反复学习，得到一系列弱分类器（基本分类器），然后组合这些弱分类器，构成一个强分类器。（三个臭皮匠顶个诸葛亮）

提升（boosting）方法需要解决的问题： - 如何获得更多的弱分类器————如何改变训练数据的权值或概率分布————提高被前一轮错误分类样本的权值，降低被正确分类样本的权值。 - 如何将弱分类器合成一个强分类器————加权多数表决：加大误差小的分类器的权值，减小误差大的分类器的权值。

提升方法有很多，最具代表性的就是AdaBoost算法。

AdaBoost算法

假设给定一个二分类训练数据集\(T=\\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\\}\)

其中，每个样本点由【特征+标签】组成

特征：$x_iX R^n $

标签：\(y_i \in Y={-1,+1}\)

AdaBoost利用以下算法，从训练数据中学习一系列弱分类器或基本分类器，并将这些弱分类器线性组合成一个强分类器

输入:

  • 数据集\(T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}\)
  • 弱学习算法

输出：最终分类器\(G(x)\)

步骤： 1. 初始化训练数据的权值(每个都设为1/N)： \[D_1=(w_{11},w_{1i},...,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,...,N\] 其中\(w_{ki}\) 代表迭代第k次时，第i个样本被抽到的概率！！！ 2. 对\(m=1,2,...,M\): 使用带权值\(D_m\)的训练集学习，得到基本分类器\(G_m(x):X\rightarrow \\{-1,+1\\}\) 计算\(G_m(x)\)在训练集上的分类误差率：\[e_m=P(G_m(x_i)\neq y_i)=\sum_{n=1}^N w_{mi}I(G_m(x_i)\neq y_i)\] 3. 计算\(G_m(x)\)的系数：\[\alpha_m=\frac{1}{2}log\frac{1-e_m}{e_m}\] 4. 更新训练集权值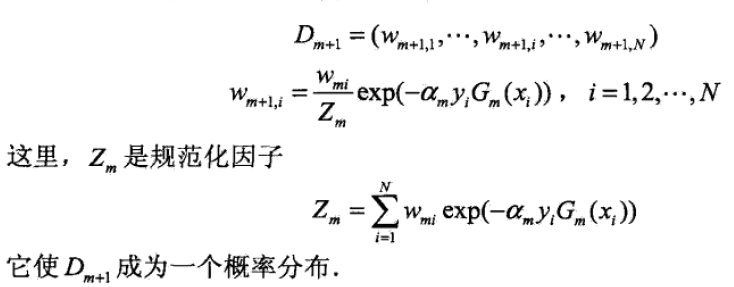： 5. 将上面迭代k次后，得到M个基本分类器。构建基本分类器的线性组合：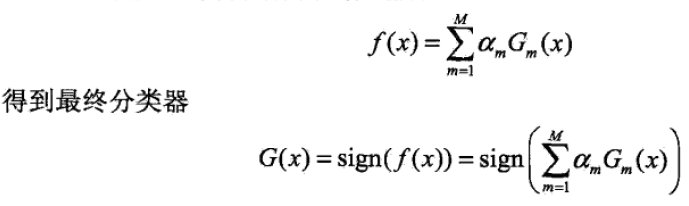

AdaBoost详解

Boot strapping

Boot strapping，拔靴法：利用有限的样本资料经由多次重复抽样，重新建立起足以代表母体样本分布之新样本。

多次之后，得到一个非线性的结果（黑色线）

基本算法引入权重

已知：一笔数据\(D={(x_1,y_1),(x_2,y_2),(x_3,y_3),(x_4,y_4)}\)。根据D算出来的输入误差Ein为：

通过Boot strapping，得到新的一笔数据\(D_t={(x_1,y_1),(x_1,y_1),(x_2,y_2),(x_4,y_4)}\)。对应地，根据Dt算出来的Ein为：（增加一个权重u即可）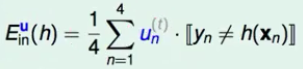

\(u1=2,u2=1,u3=0,u4=1\)

结论：每一个bootstrapping得到了一个权重u

优化权重u

优化原理

  • 每一个bootstrapping得到了一个权重u。
  • 为了综合得到更好的g,则需要抽取的数据集得到的g尽量地不同。
  • 改变u，使得g差异更大，才会更好地改进最终结果

得到g差异很大的方法：

  • 第一轮\(u_n^t\)时，得到\(g_t\)
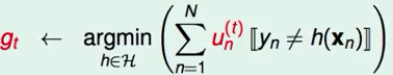
  • 第二轮，选择一个 在\(g_t\) 表现不好的 \(u_n^{t+1}\) ，得到 \(g_{t+1}\) -- 表现不好的定义： --- 将\(u_n^{t+1}\)作用在\(g_t\)上，得到一个归一化的错误率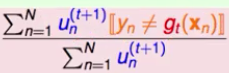 --- 为了简便，定义橙色方块为所有犯错误的\(u_n^{t+1}\)的累加，绿色圆形为所有正确的\(u_n^{t+1}\)累加 --- 即： -- 表现不好的选择方法： --- 将本次正确的\(u_n^t\)，除以一个错误的比例（缩小正确），赋给\(u_n^{t+1}\) --- 将本次错误的\(u_n^t\)，乘以一个正确的比例（放大错误），赋给\(u_n^{t+1}\) --- 这样得到的\(u_n^{t+1}\)的比率就会为2/1 --- 即：

优化权重u的方法————放缩因子

放缩因子-Adaptive Boosting Algorithm 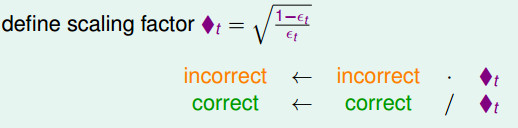- ◆t有更清晰的物理意义，通常情况下εt < 1/2（因为是学习之后的结果，错误率应该小于0.5）， - ◆t将大于1； - 那么，犯错的数据将乘上大于1的数，正确数据将除以大于1的数 - 使得提升了犯错数据的权重(scale up incorrect)， - 降低做对数据的权重(scale down correct) - 这样使得更加专注在犯了错的地方，来得到不一样的假设(diverse hypotheses)。

Linear Aggregation（聚集） - 合成最终的g

目标：合成最终的的\(G(x)=sign(\sum_{t=1}^T\alpha_t g_t(x)\) - 其中 \(\alpha_t\)是系数 - 要求好的\(g_t\)（错误率低），\(\alpha_t\)应该大一些 - 坏的\(g_t\)（错误率高），\(\alpha_t\)应该小一些 - 而◆t与错误率成反比 - 则可令\(\alpha_t=ln(\text{◆t})\)

算法流程：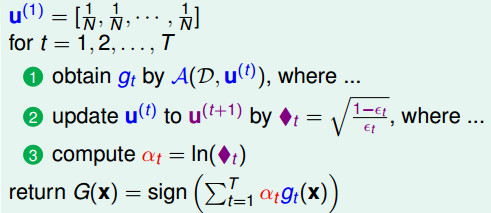

这里之所以认为αt = ln(◆t)，处于下面的考虑： 如果εt = 1/2， 那么◆t = 1，则αt = 0，意思是随机乱猜的情况下（二元分类错误率为0.5），认为是坏的g，则一票不给个，不使用该g 如果εt = 0， 那么◆t = ∞，则αt = ∞，意思是正确率为0的情况，给它无限多票数

AdaBoost 自适应优化算法总结

自适应优化算法 = 简单的学习A + 放缩权重 + 合成得到g 即：

AdaBoost算法完整流程

AdaBoost理论特性

通过之前的VC Bound，来约束测试误差，其中蓝色的部分是模型的复杂度，O(dvc(H))为g的模型复杂度，而O(dvc(H))·T·logT是模型G的复杂度。原作者证明说，可以用O(logN)次迭代可以将Ein(G)做到很小，并且当数据量N足够多的情况下，又可以使得模型复杂度变得很小，从而使得模型复杂度得到控制。最终预测效果Eout也会很好。 AdaBoost的保证是让一个很弱的算法不断变强，最终得到一个很强是算法（Ein=0，Eout is small）。 # Adaptive Boosting的实际应用表现 上面的AdaBoost只需要一个很弱的算法就可以使用。 一般情况下，可以使用决策桩(Decision Stump)，该模型相当于在某一个维度上的Perceptron模型。

聚合（aggregation）模型总结

aggregation 模型主要应用在将得到的多个预测函数\(g_t\)聚合在一起，得到更好的\(g_t\)（即更好的分类器）的方式

聚合方式主要面向两种情况：

  • blending:已经有了一堆\(g_t\)在手上（可能是已知的，可能是求得的）。
  • learning：不已知\(g_t\)，需要通过一定方式求得很多\(g_t\)

learning的分为三种情况

  • 把g看做是同等地位，通过投票或者平均的方式将它们合起来，称为Bagging
  • g是不平等的，有好有坏，一个可行的做法是把g当成是特征的转换，然后丢进线性模型训练就可以了，这称为AdaBoost
  • 如果是不同的条件下，使用不同的g，那么我们仍然可以将g当做是特征转换，接下来使用一个非线性模型来得到最终的模型参数，这就是下文要介绍的决策树算法
\(g_t\)类型 blending learning
各\(g_t\)等权重型（uniform） 投票方式/平均方式 Bagging
\(g_t\)权重不等型（non-uniform） 线性聚合 AdaBoost
不同情形用不同\(g_t\)（conditional） stacking 决策树

AdaBoost思路总结

  • 一般，数据量过少时，我们无法得到更好的g.
  • 因此我们采取BootStrapping方法，生成多个数据集，得到多个g
  • 最后合成最好的g

AdaBoost伪代码

对每次迭代：
    用buildStump()函数找到最佳单层决策树
    将最佳单层决策树加入到单层决策树数组
    计算alpha
    计算新的权重向量D
    更新累积类别估计值
    如果错误率等于0，则退出循环

参考文献 1. 《机器学习技法》，林轩田 2. Jason Ding，【机器学习基础】自适应提升 3. Jason Ding，【机器学习基础】决策树算法

备注：本节是《机器学习技法》第8章+《统计学习方法》第8章笔记