上一节中介绍了《随机森林算法》,该算法使用bagging的方式作出一些决策树来,同时在决策树的学习过程中加入了更多的随机因素。该模型可以自动做到验证过程同时还可以进行特征选择。
本节,我们结合AdaBoost+决策树算法。
AdaBoost决策树算法引入
在AdaBoost中每一轮迭代,都会给数据更新一个权重,利用这个权重,我们学习得到一个g,在这里我们得到一个决策树,最终利用线性组合的方式得到多个决策树组成的G。
======================================= AdaBoost-DTree(DD) 对于t=1,2,…,T,循环执行:
- 更新数据的权重\(u(t)\);
- 通过决策树算法\(DTree(D,u(t))\)得到\(g_t\);
- 计算\(g_t\)的投票权重\(α_t\)。
返回\(G=LinearHypo({(g_t,α_t)})\)。
========================================
问题:如何要在决策树中,加入权重ut
解决方案有两种:
- 一种是通过算法加权,在计算Ein的地方嵌入权重计算,比如AdaBoost采用的最小化加权误差;
- 另一种方法是将算法当成黑盒不变更,通过数据集加权,根据权重在bootstrap时“复制”数据,也就是加权的重采样。
AdaBoost决策树通常用后一种,即:$AdaBoost+sampling∝u^{(t)}+DTree(D_t) $
加权的决策树算法(Weighted Decision Tree Algorithm)
之前含有权重的算法中,我们在误差估计中加入了权重u:
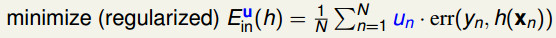
为了对决策树中加入权重,且不改变原算法的健壮性,我们设法对输入的数据进行权重加成。而权重等效于数据的重复次数。根据这种方式得到一组新的数据,那么这组新的数据中的比例大概就是和权重的比例呈正比的,也就是说它能够表达权重对于数据的意义。

在AdaBoost-DTree中,为了简单起见,我们不去改变AdaBoost的框架,也不去修改决策树的内部细节,而只是通过基于权重的训练数据的采样来实现。
即如下图所示的:AdaBoost提升决策树=AdaBoost提升+关于权重u的数据抽样+决策树

弱决策树算法
在AdaBoost算法中,我们通过错误率εt来计算单个的g的权重αt,那么如果我们使用决策树作为g的时候,g是一个完全长成的树,该树对整个数据集进行细致的切分导致Ein=0,那么这使得εt=0,但计算得到的权重αt会变成无限大。
其意义是,如果使用一个能力很强的树作为g的话,那么该算法会赋予该树无限大的权重或票数,最终得到了一棵“独裁”的树(因为AdaBoost的哲学意义是庶民政治,就是集中多方的意见,及时有的意见可能是错误的),违背了AdaBoost的宗旨。
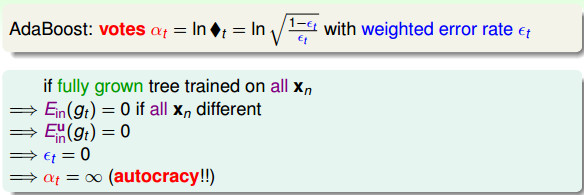
上面的问题出在使用了所有的数据和让树完全长成这两方面。针对这两个问题,我们要通过剪枝和部分训练数据得到一个弱一点的树。 所以实际上,AdaBoost-DTree是通过sampling的方式得到部分训练数据,通过剪枝的方式限制树的高度,得到弱一点的决策树。
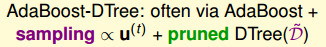
下面介绍最弱的决策树。
决策桩,AdaBoost-Stump
什么样是树才是弱决策树呢? 我们这里限制这棵树只有一层(即它仅基于单个特征来做决策),即决策桩(Decision Stump)。这样我们需要让CART树的不纯度(impurity)尽可能低,学习一个决策桩。

所以,使用决策桩作为弱分类器的AdaBoost称为AdaBoost-Stump,它是一种特殊的AdaBoost-DTree。
决策桩的实现
本节主要参考《机器学习实战》p120
实验数据adaboost.py
from numpy import *
def loadSimpData():
dataMat = matrix([[1.,2.1],[2.,1.1],[1.3,1.],[1.,1.],[2.,1.]])
classLabels = [1.0,1.0,-1.0,-1.0,1.0]
return dataMat,classLabels二分类的决策桩实现stump.py
先导入数据
import adaboost
dataMat,classLabels = adaboost.loadSimpData()建立一个buidStump()函数,根据数据集,建立最佳单层决策树(只需要选择一个最好的特征即可)
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr)
labelMat = mat(classLabels).T # T是做转置dataMatrix形式为
labelMat形式为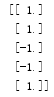
先令一些变量,之后解释。
m,n = shape(dataMatrix)
numSteps = 10.0#步长
bestStup = {}#最佳桩
bestClasEst = mat(zeros((m,1)))#最佳分类est
minError = inf接下来需要对每个特征计算出一个阈值threshVal,根据阈值二分类。
for i in range(n): # 遍历特征个数
#为了确定threshVal,我们从本特征下的最小值到最大值分10 step进行依次测试
rangeMin = dataMatrix[:,i].min();rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax - rangeMin)/numSteps
#下面对每个threshVal可能的值进行依次测试
for j in range(-1,int(numSteps)+1):
#然后应该开始比较大于阈值和小于阈值怎么怎么滴,为了增加代码的复用性,此处用一个循环来在大于和小于之间切换不等式
for inequal in ['lt','gt']:#lt=小于等于,gt=大于
threshVal = (rangeMin + float(j)*stepSize)
# 开始测试这个特征下这个阈值的二分类器好不好用
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)
#计算本次分类的err
errArr = mat(ones((m,1)))
errArr[predictedVals==labelMat]=0
#基于权重向量D计算权重
weightedError = D.T*errArr
if weightedError < minError :
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal最后,返回最佳的决策桩,和误差
return bestStump,minError,bestClasEst求解AdaBoost决策树
AdaBoost的权重与投票分数的关系
回顾AdaBoost算法:
从权重ut,通过◆t对u(t+1)进行修正,而两个公式可以合成为: 
如下图,接着我们将u(t+1)展开(表达为u(1)乘以一坨),最终可以变成连加; 我们发现图中橘色部分∑αt·gt(xn)是G(x)的分数!它现在出现在Adaboost的权重表达式中; 我们称橘色∑αt·gt(xn)为投票分数(voting score): 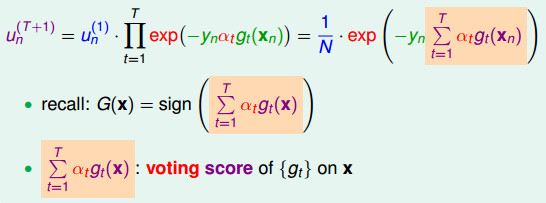
结论:AdaBoost里面每一个数据的权重,和exp(-yn( 投票分数 on xn))呈正比。即: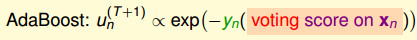
投票分数(Voting Score)和间隔(Margin)的关系
线性混合(linear blending)等价于将假设看做是特征转换的线性模型:

其中αt·gt(xn)如果换作是wT·φ(xn)可能就更清楚了,这与下面给出的在SVM中的margin表达式对比,我们可以明白投票分数∑αt·gt(xn)的物理意义,即可以看做是没有正规化的边界(margin)。

所以,yn·(voting score)是有符号的、没有正规化的边界距离,从这个角度来说,我们希望yn·(voting score)越大越好,因为这样的泛化能力越强。于是,exp(-yn·(voting score))越小越好,那么un(T+1)越小越好。

结论:AdaBoost在迭代过程中,是让∑un(t)越来越小的过程,在这个过程中,逐渐达到SVM中最大分类间隔的效果。
AdaBoost误差函数
上面解释到了,AdaBoost在迭代学习的过程,就是希望让∑un(t)越来越小的过程,那么我们新的目标就是最佳化权重和∑un(T+1):
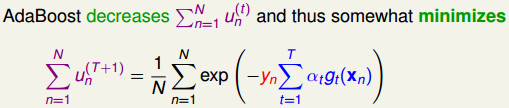
我们可以画出0/1错误和AdaBoost误差函数err(s,y) = exp(-ys)的函数曲线,我们发现AdaBoost的误差函数(称为exponential error measure)实际上也是0/1错误函数的上限函数,于是,我们可以通过最小化该函数来起到最佳化的效果。

AdaBoost误差函数的梯度下降求解
本节目的————最小化AdaBoost的误差函数Ein:
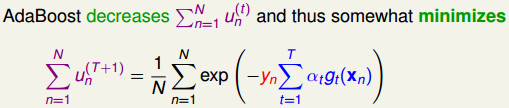
这个任务比较麻烦,因为是Σ套着exp再套着Σ,因此需要一些前人的智慧了。
我们可以将Ein函数在所在点的附近做泰勒展开,我们就可以发现在该点的附近可以被梯度所描述,我们希望求一个最好的方向(最大梯度相反的方向),然后在该方向上走一小步,这样我们就可以做到比现在的函数效果好一点点,依次进行梯度下降,最终达到最小化误差函数的效果。
原始的梯度下降法:
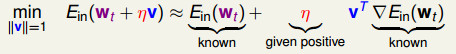
为了模仿梯度下降的方法,假设前面已经AdaBoost完t-1轮了,现在要求的是一个函数gt(x)(或者称为h(x))。
在第t轮,我们沿着函数h(x)的方向走\(η\)的步长,可以使得目标函数迅速往min的方向走。如下:现在我们把函数gt当做向量,希望去找到这个gt(这里函数方向gt和上面介绍的最大梯度的方向向量没有什么差别,只是表示方式有所不同而已)。
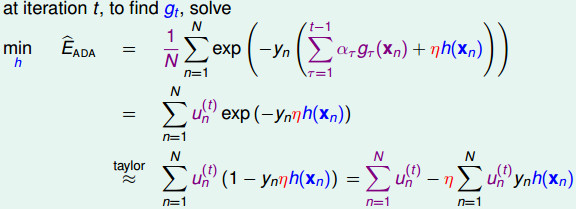
我们解释一下上面的公式:
- (1、2行)由于前面已经执行完了
t-1轮,因此可以把式子化简一下,把一些项目合并成ut的函数形式 - (3行左) 将
exp(-y·η·h(xn))在原点xn=0点的泰勒展开,进一步化简得到得到(1-yn·η·h(xn));(这里为什么要用0这个位置的taylor展开呢,可以理解成h(x)只是沿着原来的Σ1,t-1(alphat*g'(xn)这个函数,挪动的了一小步;这一小步,就意味着变化很小,变化很小甚至接近0,因此就可以在0点taylor展开。不晓得这种理解是否正确,意会吧) - (3行右) 然后拆成两部分
∑un(t)和η·∑un(t)·yn·h(xn),第一部分是Ein,第二部分就是要最小化的目标。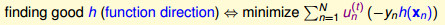
到此,我们利用前人的智慧已经把目标函数给大大简化了,下面需要要求的东西有俩:
1)h(x)是啥?
2)$η$是啥?
求h(x)
我们对∑un(t)·yn·h(xn)整理一下,对于二元分类情形,我们把yn和h(xn)是否同号进行分别讨论:

上面的公式中,我们特意将∑un(t)·yn·h(xn)拆成-∑un(t)和Ein(h)的形式,这里最小化Ein对应于AdaBoost中的A(弱学习算法),好的弱学习算法就是对应于梯度下降的函数方向。
结论:在AdaBoost的过程中,算法A就是good gt了!
求最佳化步长\(η\)
我们要最小化Eada,需要找到好的函数方向gt,但是得打这个gt的代价有些大,梯度下降的过程中,每走一小步,就需要计算得到一个gt。如果转换一下思路,我们现在已经确定了好的gt,我们希望快速找到梯度下降的最低点,那么我们需要找到一个合适的最大步长η。 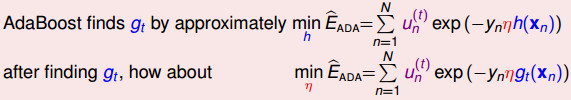
我们这里使用贪心算法来得到最大步长η,称为steepest decent for optimization。

让Eada对η求偏微分,得到最陡时候的ηt,我们发现这时ηt等于AdaBoost的αt。所以在AdaBoost中αt是在偷偷地做最佳化的工作。
核心在于EADA是怎么变成可对\(η\)求导的形式的:
EADA = u1texp(-\(η\)) + u2texp(\(η\))...
EADA1 = u1texp(-\(η\)) + ut2t0 ... (EADA1只考虑exp(-\(η\))的项,其余的补上0)
EADA2 = u1t0 + u2t exp(\(η\)) ...(EADA2只考虑exp(+\(η\))的项,其余的补上0)
则,EADA = EADA1 + EADA1 = (Σunt) * ( (1-epson)exp(-\(η\)) + epson*exp(\(η\)) )
随后的求导步骤就是很自然的了,因此就验证了之前的结论,\(η\)t = sqrt( (1-epsont)/epsont) )就是最优的。前一次课直接给出了这个结论,并没有说为什么,这次算是给出了一个相对理论些的推导。
结论:通过求解 ,我们得到最佳的
,我们得到最佳的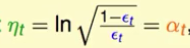
小结
在第二小节中,我们从另外一个角度介绍了AdaBoost算法,它其实是steepest gradient decent。
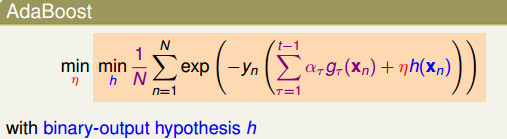
上面的式子很清楚了,我们将AdaBoost的误差函数看做是指数误差函数,AdaBoost就是在这个函数上一步一步做最佳化,每一步求得一个h,并将该h当做是gt,决定这个gt上面要走多长的距离ηt,最终得到这个gt的票数αt。
AdaBoost决策树总结
- AdaBoost本次的u(t+1)与
exp(-yn( 投票分数 on xn))成正比 - AdaBoost在迭代过程中,是让
∑un(t)越来越小的过程,在这个过程中,逐渐达到SVM中最大分类间隔的效果 - 上目标与最小化误差函数
err(s,y) = exp(-ys)等价 - 要使得
err(s,y)最小,就需要求得h(x)和η