之前的AdaBoostDTree的误差函数是指数型的。GBDT的误差函数是任意指定的。GBDT的核心就在于,每一棵树学的是之前所有树结论和的残差,这个残差就是一个加预测值后能得真实值的累加量。
GBDT的误差函数

- 紫色部分:之前学过的所有树的结果叠加
- 红色和蓝色部分:本轮学习的模型
- 将之前学习的树与本轮学习的模型叠加,就得到了本次的预测值
目标
- 求函数h(x)的形式
- 求h(x)的步长η
回归问题求解目标
对于回归(regression)问题,误差函数一般采用平方误差。即:

为了进一步求解,我们对上式进行taylor展开,即:
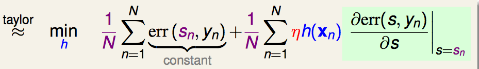
其中: - 左边一项\(err(S_n,y_n)\)是常量(因为\(S_n\)、\(y_n\)都已知) - 右边一项应该对s求导,并在sn这点取导数值(\(error=(s-y)^2\)求导之后得到\(2(s-y)\))
那么,上式等于:
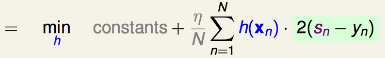
求h(x)
为了让上式最小化,那么貌似\(|h(x)|\)无穷大即可实现,这不科学!于是我们要对\(h(x)\)的大小进行限制(类似归一化)————加入惩罚项\((h(x_n))^2\),即将上式变为:
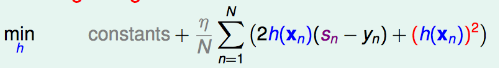
而上式可变为:

其中的\((s_n-y_n)^2\)是常数,记为constant
那么新的目标就变为:用\(x_n\)和\(y_n-s_n\)做一个regression即可。即:

经过penalize一番折腾之后,h终于有个像模像样的形式了:即regression with residuals(残差)。
求步长η
需要求得一个η,使得下式最小化:

为了方便计算,我们将平方内的项取负:
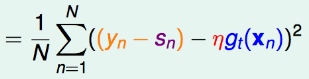
上式的\(y_n-s_n\)即residuals(残差).这是一个单变量的线性回归问题,其中输入是用gt转换后的数据,输出是残差(residual)。
GBDT算法
输出:\(\sum_t^T\alpha_t g_t(x)\),即一堆权重\(\alpha_t\)和一堆决策树\(g_t(x)\) 步骤: 
1)利用C&RT去学{x, yn-sn},保留这一轮学出来的树gt(x)
2)再求{gt(x), residual}线性回归,最小化目标函数求出来ita
3)更新sn
学习足够多次数后,返回组合的GBDT。