单源最短路径问题:给定一个图 \(G=(V,E)\) ,我们希望找到从给定源节点\(s\in V\)到每个节点\(v \in V\)的最短路径。
先总结:
Bellman-Ford算法:采用动态规划进行设计。待总结。简单,还能侦探含源节点的负权重回路。 Dijkstra算法:采用贪心算法范式进行设计。复杂度低,但要求权重非负。
最短路径树
一颗根节点为s的最短路径树是一个有向子图\(G'=(V',E')\),这里\(V'\in V\),\(E'\in E\),满足: 1. \(V'\)是图G中从源节点s可以到达的所有结点的集合; 2. \(G'\)形成一颗根节点为s的树; 3. 对于所有结点\(v\in V'\),图\(G'\)中从结点s到结点v的唯一简单路径是图G中从结点s到结点v的一条最短路径。
松弛操作
对每个节点v,我们维持一个属性v.d,记录s→v的最短路径估计
松弛操作:比较s→u→v与s→v的d,然后进行更新。
RELEAX(u,v,w)
if v.d>u.d+w(u,v)
v.d=u.d+w(u,v)
v.π=uBellman-Ford算法
目标:解决单源最短路径问题 条件:边权重可负 输入:带权有向图\(G=(V,E)\)和权重函数\(w:E→R\) 输出:布尔值,是否存在一个从源节点可以到达的负权重回路。若存在,则算法无解。
思路:Bellman-Ford通过对边进行松弛操作来渐进地降低从源节点s到每个节点v的最短路径估计值v.d,直到该估计值与实际的最短路径权重\(δ(s,v)\)相同为止。
初始函数:
INITIALIZE-SINGLE-SOURCE(G,s)
for eahc vertex v∈G.V
v.d=∞
v.π=null
s.d=0算法:
BELLMAN-FORD(G,w,s)
INITIALIZE-SINGLE-SOURCE(G,s)//对每个点v.d和v.π初始化
for i=1 to |G.V|-1 //对每个边处理V-1次
for each edge(u,v)∈G.E //遍历所有的边
RELAX(u,v,w)
for each edge(u,v)∈G.E
if v.d>u.d+w(u,v)
return False
else
return True复杂度:\(O(VE)\)
对每个边处理V-1的原因:设p是从s到v的最短路径,则p最多包含V-1条边。
如下图所示的极限条件,v0-v5路径应该为<v0,v1,v2,v3,v4,v5>
原本v0-v5的路径是灰色的。 第一轮松弛后,v0-v5路径变为<v0,v1,v5>,即黑色的 同理,第二轮松弛后,v0-v5路径变为<v0,v1,v2,v5> 因此要松弛V-1次才可以 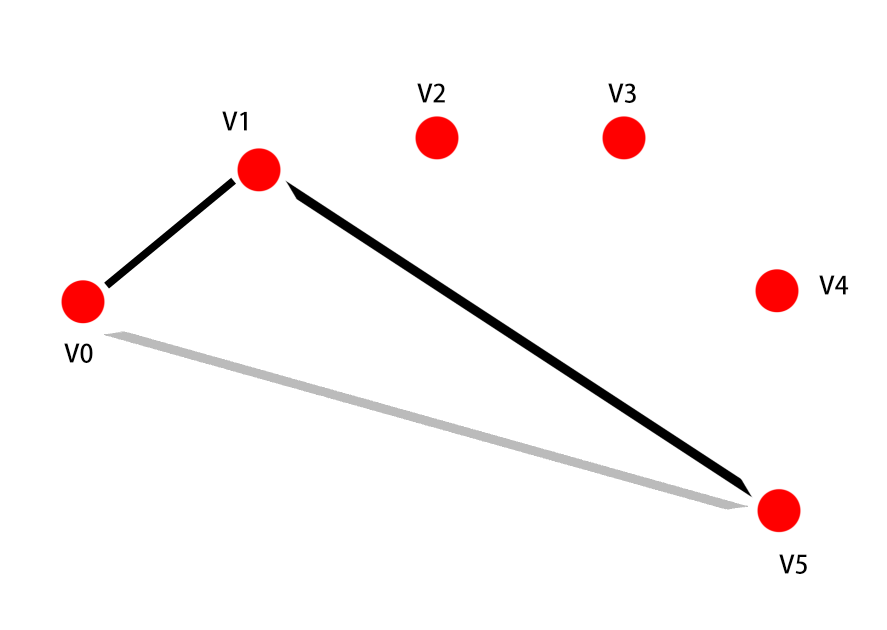
Dijkstra算法
条件:所有边的权重非负 思想:由上述性质可知,如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。即:每次找到离源点最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。
Dijkstra算法的关键:维持一组节点集合S,从s到该集合中的每个节点的最短路径已经被找到。算法重复从V-S中选择最短路径估计最小的节点u,将u加入结合S,然后对所有从u出发的边进行松弛。
DIJKSTRA(G,w,s)
INITIALIZE-SINGLE-SOURCE(G,s)//对v.d和v.π初始化
S={}
Q=G.V
while Q.length != 0
u = UXTRACT-MIN(Q)//从V-S中选出最短路径估计最小的节点u
S=S∪{u}
for each vertex v∈G.Adj[u]
RELAX(u,v,w)算法解释 二维数组 e 来存储顶点之间边的关系,初始值如下: 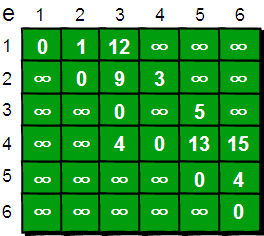
我们还需要用一个一维数组 dis 来存储 1 号顶点到其余各个顶点的初始路程,如下。 我们将此时 dis 数组中的值称为最短路的“估计值” 
图的关系如图所示,1是源点
既然是求 1 号顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离 1 号顶点最近是 2 号顶点。当选择了 2 号顶点后,dis[2]的值就已经从“估计值”变为了“确定值”,即 1 号顶点到 2 号顶点的最短路程就是当前 dis[2]值。 原因:目前离 1 号顶点最近的是 2 号顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 1 号顶点到 2 号顶点的路程进一步缩短了。因为 1 号顶点到其它顶点的路程肯定没有 1 号到 2 号顶点短,
既然选了 2 号顶点,接下来再来看 2 号顶点有哪些出边呢。有 2->3 和 2->4 这两条边。先讨论通过 2->3 这条边能否让 1 号顶点到 3 号顶点的路程变短。也就是说现在来比较 dis[3]和 dis[2]+e[2][3]的大小。其中 dis[3]表示 1 号顶点到 3 号顶点的路程。dis[2]+e[2][3]中 dis[2]表示 1 号顶点到 2 号顶点的路程,e[2][3]表示 2->3 这条边。所以 dis[2]+e[2][3]就表示从 1 号顶点先到 2 号顶点,再通过 2->3 这条边,到达 3 号顶点的路程。
我们发现 dis[3]=12,dis[2]+e[2][3]=1+9=10,dis[3]>dis[2]+e[2][3],因此 dis[3]要更新为 10。这个过程有个专业术语叫做“松弛”。即 1 号顶点到 3 号顶点的路程即 dis[3],通过 2->3 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛 1 号顶点到其余各个顶点的路程。
同理通过 2->4(e[2][4]),可以将 dis[4]的值从 ∞ 松弛为 4(dis[4]初始为 ∞,dis[2]+e[2][4]=1+3=4,dis[4]>dis[2]+e[2][4],因此 dis[4]要更新为 4)。
刚才我们对 2 号顶点所有的出边进行了松弛。松弛完毕之后 dis 数组为: 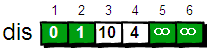
以此类推,此处不再多加阐述。
有向无环图的单源最短路径问题
来日再填坑。