LU分解:可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积（有时是它们和一个置换矩阵的乘积）。LU分解主要应用在数值分析中，用来解线性方程、求反矩阵或计算行列式。
LU分解条件
如果n阶方阵A的各阶顺序主子式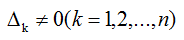
，即A的各阶顺序主子矩阵Ak都可逆，则存在唯一的单位下三角矩阵L与唯一的非奇异上三角矩阵U，使得A=LU
其中k阶顺序主子式指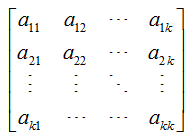 
LU分解方法
由于L存在可逆矩阵L'，即LL'=E 则L'A=LL'U=U 因此得出一般的分解方法： 通过对(A,E)做初等行变换得到(U,L'),再由L'得到L.
其中：
- L是单位下三角矩阵（对角线上的系数都为1的下三角矩阵）；L'也是单位上三角矩阵；
- U是非奇异上三角矩阵；
直接消去法的矩阵解释
计算过程如图所示：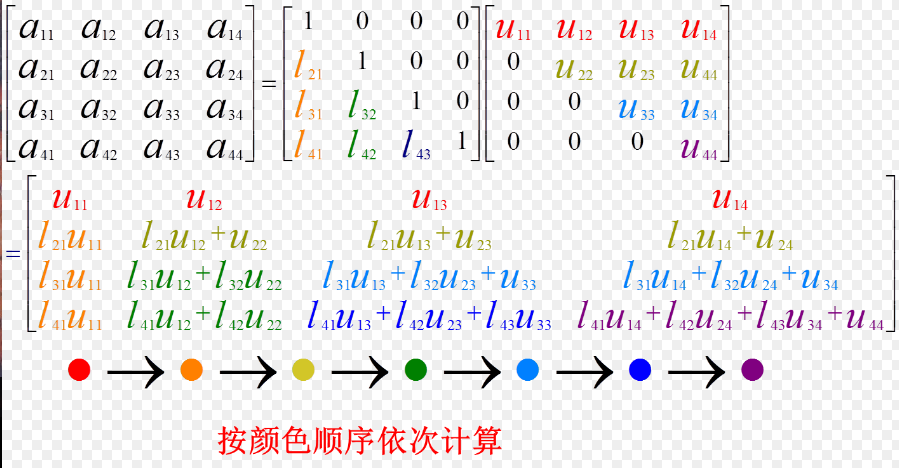 
目的：将[A|E]-->[U|L]形式，其中U是上三角矩阵
过程：每轮将一列的下三角消为0，就相当于给A左乘一个下三角单位矩阵Lk（对角线为1，保证变换后对角线元素不变）。
第一轮消元：将第一列的下三角消为0，相当于对A1左乘矩阵L1，即：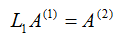
其中， 
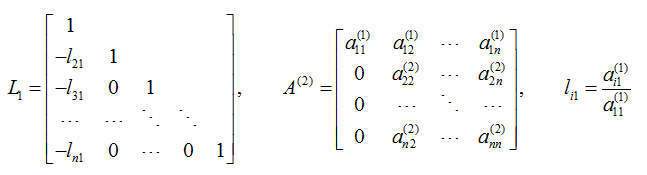我们注意到li1恰好使得第i行的第一列元素变为零，即ai1-li1*a11=0。
第二轮消元：将第二列的下三角消为0，对应于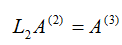
第k轮消元: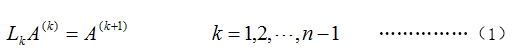
其中，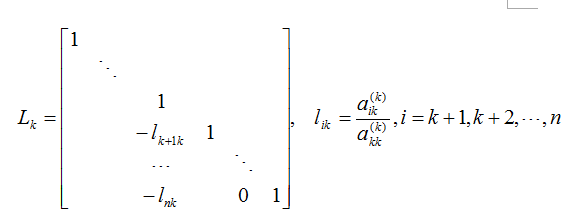
把k轮消元相乘，即： 整个消元过程为： 
总结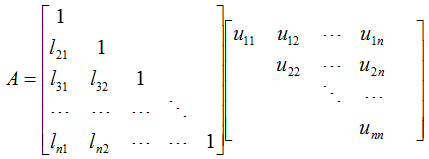 
初始（第一步）： 
迭代第r步： 即 ur=f(u1,u2,...,u(r-1),l1,l2,...,l(r-1)),第r项由前r-1项计算得到 lr=g(u1,u2,...,u(r-1),l1,l2,...,l(r-1)) 
计算顺序：
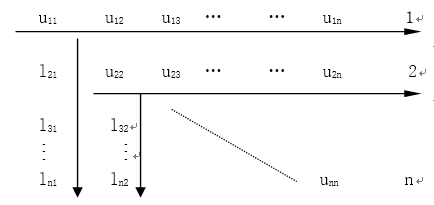
需要注意的是，我们在计算时需要判断本阶的顺序主子式是否为零。
代码实现 备注：其中的piovt暂时没有卵用。
输入矩阵：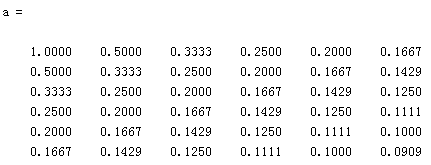
bool lu(double *a,int *pivot,int n){//矩阵是n*n的
double test = det(a,r,n);//检验本阶顺序主子式是否为0
if(test==0){
return true;
}
//数组a在内存中按行优先次序存放
//pivot:输出参数
//pivot[0,n)中存放主元的位置排列
//成功时返回false，否则返回ture
//int len = sizeof(a)/sizeof(a[0]);
double *U,*L;
U = new double[n*n];
L = new double[n*n];
set0(U,n);
set0(L,n);
//先算urj(固定r，计算完所有的urj)，再算ljr(固定i，计算完所有的ljr)
for(int r=0;r<n;r++){
//计算urj(固定r，计算完所有的urj)
//计算ljr(固定i，计算完所有的ljr)
for(int j=r;j<n;j++){
double sum_lu1=0;
double sum_lu2=0;
for(int k=0;k<r;k++){
sum_lu1 = sum_lu1+L[r*n+k]*U[k*n+j];
sum_lu2 = sum_lu2+L[j*n+k]*U[k*n+r];
}
U[r*n+j]=a[r*n+j]-sum_lu1;
if(j==r){
L[j*n+r]=1;
}else{
L[j*n+r]=a[j*n+r]-sum_lu2;
L[j*n+r]=L[j*n+r]/U[r*n+r];
}
}
}
return false;
}结果： 
不知道为什么，我的答案与网上的之前学长做过的这道题的答案统统不一样。仔细检查后还是查不出来。又用Matlab验证了一下LU分解，MATLAB跑的结果为：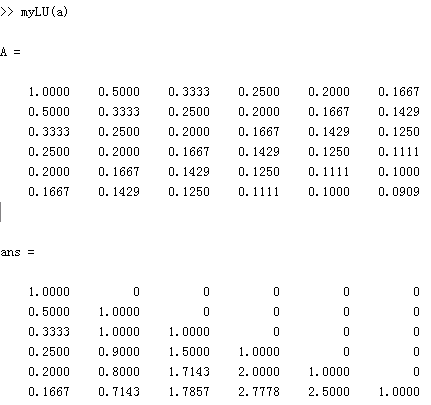 
与我自己的L矩阵一致。决定还是相信自己。
列主元高斯消去法
主要思想是在每次计算第r行时，选取当前第r列下的最大的a[i,r]的所在的第i行作为主元，即将第i行与第r行交换，再进行计算。
主要理论见参考文献-北邮理学院数值分析课件chapter5.
代码：
#include <iostream>
#include<cstdio>
#include<cstdlib>
#include<iomanip>
#define LIM -100000000
using namespace std;
double *luReult;
void printmat(double *mat,int n,string s){
std::cout<<endl<<endl<<s<<endl;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
printf("%.5f\t",mat[i*n+j]);
}
std::cout<<endl;
}
}
void printarr(int *mat,int n,string s){
std::cout<<endl<<endl<<s<<endl;
for(int i=0;i<n;i++){
std::cout<<mat[i]<<"\t";
//printf("%s\t",mat[i]);
}
}
int findMainNumber(double *a,int n,int r){
float maxa=-99999;
int maxaIdx=-1;
//printmat(a,n,"a is now :");
for(int i=r;i<n;i++){
if(a[i*n+r]>maxa){
maxa=a[i*n+r];
maxaIdx=i;
}
}
return maxaIdx;
}
void exchange(double *a,int n,int e,int r){
float temp=0;
for(int i=0;i<n;i++){
temp = a[r*n+i];
a[r*n+i]=a[e*n+i];
a[e*n+i]=temp;
}
}
bool lu(double* a, int* pivot, int n)//矩阵LU分解
{
for(int k=0;k<n;k++){
//寻找第k列的主元
int p = findMainNumber(a,n,k);
exchange(a,n,p,k);//交换k行和p行
pivot[k]=p;//记录置换矩阵p
if(a[k*n+k]!=0){
for(int i=k+1;i<n;i++){//部分下三角L
a[i*n+k]=a[i*n+k]/a[k*n+k];
}
for(int i=k+1;i<n;i++){//计算上三角U
for(int j=k+1;j<n;j++){
a[i*n+j]=a[i*n+j]-a[i*n+k]*a[k*n+j];
}
}
}else{
return true;//矩阵奇异
}
}
/*
//计算下三角L
double temp=0;
for(int i=0; i<n-2; i++)//i行k列
for(int k=i+1; k<n-1;k++)
{
temp=a[n*pivot[k] + i];
a[n*pivot[k] + i]=a[k*n + i];
a[k*n + i]=temp;
}
*/
luReult=a;
printmat(a,n,"lu");
return false ;
}
double radio(int a,int b){
return (double)(a)/(double)(b);
}
void buildHilbert(double *a,double *b,int n){
for(int r=0;r<n;r++){
for(int j=0;j<n;j++){
a[r*n+j]=radio(1,j+r+1);
b[r]=b[r]+a[r*n+j];
}
}
}
void exchangeb(double *b,int n,int r,int e){
double temp=0;
temp=b[e];
b[e]=b[r];
b[r]=temp;
/*r(int i=0;i<n;i++){
temp=b[r*n+i];
b[r*n+i]=b[e*n+i];
b[e*n+i]=temp;
}*/
}
int main()
{
int n=6;//矩阵是n*n的
double *b=new double[n];
double *a=new double[n*n];
/*double input[n*n]={0.001,1.00,1.00,2.00};
a=input;
double inputb[n]={1.00,3.00};
b=inputb;*/
buildHilbert(a,b,n);
printmat(a,n,"a:");
int *pivot=new int[n*n];
luReult=new double[n*n];
lu(a,pivot,n);
printarr(pivot,n,"p:");
//cout << "Hello world!" << endl;
return 0;
}输出： 