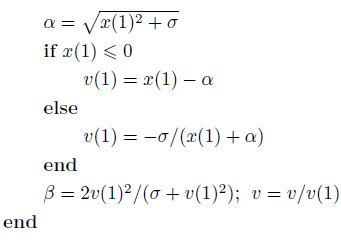QR分解
引理：
- 对于任意的\(A\in C^{n\times n}\),若存在\(n\)阶正交矩阵\(Q\)和\(n\)阶上三角矩阵\(R\)，使得\(A=QR\)，则称\(QR\)为\(A\)的\(QR\)分解。
- 若\(A\in C^{n\times n}\)可逆，则存在正交矩阵\(Q\)和正对角元的上三角矩阵\(R\)，使得\(A=QR\)，且表示式唯一。
备注：正交矩阵：\(A^{-1}=A^T\) QR分解定理：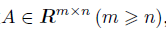
，则A有QR分解：
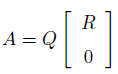Q是mm的正交矩阵 R是nn的有非负对角元的上三角阵
当m=n，且A非奇异时，上述分解唯一。
计算QR分解的方法 
备注： 计算A(j:m,j:n)=(I(m-j+1)-bvvT)A(j:m,j:n)时， I(m-j+1)-bvvT可以表示为：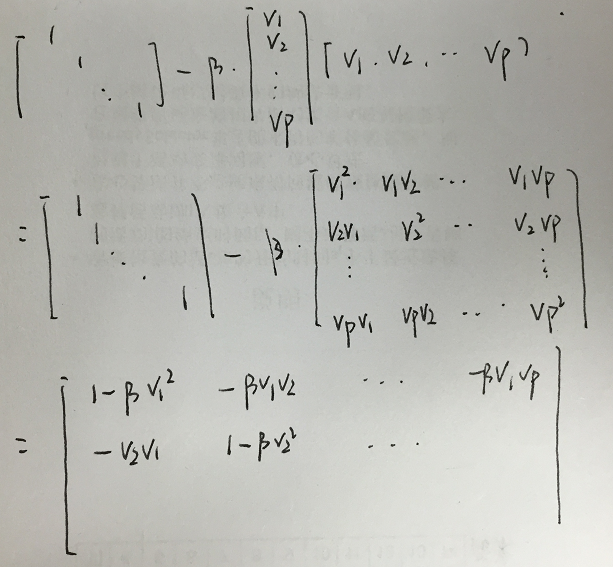 
QR分解的存储方法 
用QR分解解线性方程组 \(Ax=b\) \(QRx=b\) \(Rx=Q^{-1}b\) \(x=R^{-1}Q^{-1}b\) \(x=R^{-1}Q^Tb\)
householder方法
利用Householder变换逐步将A化为上三角矩阵。
使用Gauss变换将矩阵化为上三角的理论依据————对于一个给定的向量x，可构造一个初等下三角阵L，使得\(Lx=ae_1\)，其中\(e_1\)是I的第一列，a是实数。（I是单位矩阵）
householder变换目的： 求一个初等正交矩阵，使其具有矩阵L的功能。
使得： 可以通过一系列初等正交变换来完成矩阵的上三角化任务。
Householder变换 
其中： I是单位矩阵 w是实的单位列向量（单位正交矩阵），\(ww^T=I\)
HouseHolder变换可以将一个向量映射到一个超平面上。
Householder变换的性质
- 对称性。\(H^T=H\)
- 正交性。\(H^TH=I\)
- 对合性。\(H^2=I\)
- 反射性(householder变换的物理意义)：
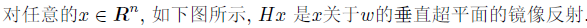
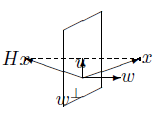
Householder变换的用途
它能如Gauss变换一样，可以通过适当选取单位向量w，把一个给定向量的若干指定的分量变为零。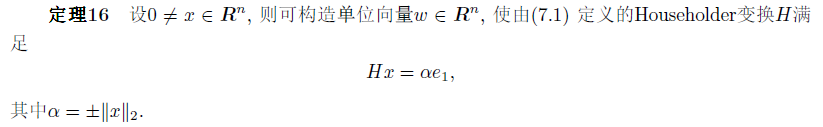 
由以上定理可知，对于任意的x，都可以构造出Householder矩阵H，使得Hx的后n-1个分量为零。
Householder变换方法 计算某一行向量的houser变换： 
