特征选择:很重要
tip:冗余特征(redundant feature): - 本特征能被其它特征中推演出来。它不一定有坏处,但也不一定有好处。例如:考虑立方体对象,若已有特征“长”、“宽”,则“底面积”是冗余特征。 - 冗余特征在很多时候不起作用,会增加学习过程的负担。 - 但如果学习目标是估算立方体体积,则“底面积”特征会对学习更好。
结论:如果某冗余特征恰好对应完成学习任务所需的“中间概念”,则该冗余特征是有益的。
子集搜索与评价
特征选取时,若没有任何领域知识进行先验假设,只能遍历所有可能子集。-->不可取!
可行做法: 产生个“候选子集”,评价它的好坏,基于评价结果产生下一个候选子集。
问题一,如何评价结果获取下一个候选特征子集?
子集搜索
- 前向搜索
- 给定特征集合\({a_1,a_2,...,a_d}\),将每个特征看做一个候选子集。对d个候选单特征子集进行评价,假定\({a_2}\)最优,将\({a_2}\)做为第一轮选定集;
- 加入一个新特征,构成包含两个特征的候选子集,假定在这\(d-1\)个候选两特征子集中\({a_2,a_4}\)最优,则将\({a_2,a_4}\)作为本轮选定集;
- ...
- k+1轮时,不再更好,停止迭代
- 后向搜索 每次都删除掉一个特征
问题二,如何评价候选特征子集?
信息增益
- 给定数据集\(D\),假定\(D\)中第\(i\)类样本所占的比例为\(p_i(i=1,2,...,|Y|)\).
- 假定所有样本属性均为离散型
- 对属性子集\(A\),假定根据其取值将\(D\)分成了\(V\)个子集\({D^1,D^2,...,D^V}\),每个子集中的样本在A上取值相同,则属性子集\(A\)的信息增益为:
\[Gain(A)=Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)\]
其中信息熵定义为:
\[Ent(D)=-\sum_{k=1}^{|y|}p_klog_2p_k\]
信息增益\(Gain(A)\)越大,特征子集A包含的有助于分类的信息越多。
总结
特征选择方法=子集搜索+子集评价
常见特征选择方法: - 过滤式(filter) - 包裹式(wrapper) - 嵌入式(embedding)
过滤式选择(filter)
概念:先特征选择,再训练模型
特点:特征选择与模型学习无关
===来日填坑===
包裹式选择
概念:把最终将要使用的学习器的性能作为特征子集的评价准则
特点:需要多次训练学习器
===来日填坑===
嵌入式选择与L1正则化
概念:将特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成
给定数据集\(D={(x_1,y_1),(x_2,y_2),...(x_m,y_m)}\),其中\(x\in R^d,y\in R\).
考虑最简单的线性回归,以平方误差为损失函数,则优化目标为:
\[min_w\sum_{i=1}^m(y_i-w^Tx_i)^2\]
当样本特征很多,而样本数较少时,上式很容易陷入过拟合。解决方案,正则化项。
\(L_2\)范数正则化(“岭回归”(redge regression)):
\[min_w\sum_{i=1}^m(y_i-w^Tx_i)^2+\lambda ||w||_2^2\]
\(L_1\)范数正则化:
\[min_w\sum_{i=1}^m(y_i-w^Tx_i)^2+\lambda ||w||_1\]
区别:\(L_2\)比\(L_1\)更容易获得“稀疏”(sparse)解,即它求得的\(w\)会有更少的非零分量。 (这里一定要看一下西瓜书-253页的解释)
正则化的理解
以以下的拟合为例: 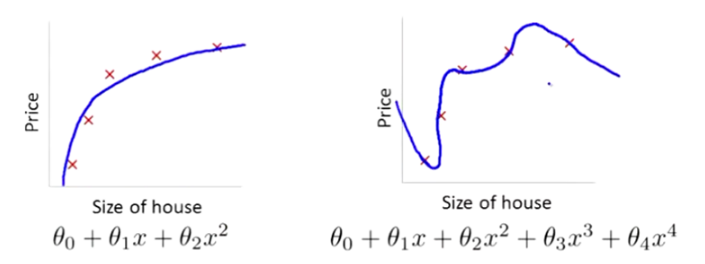
在图二中,明显是因为高次项的系数\(\theta_3,\theta_4\)过大造成的。
因此我们加入正则化项: 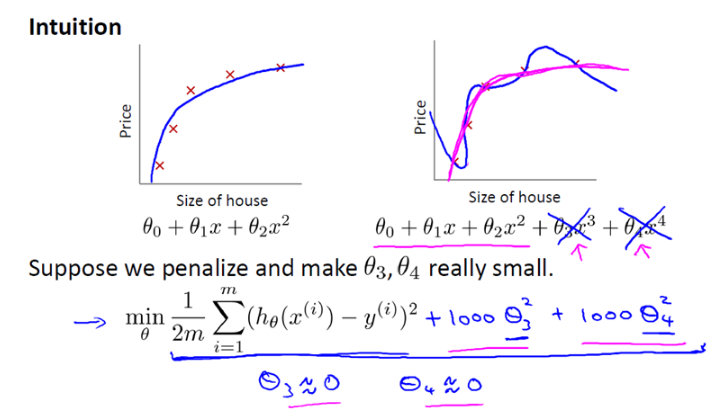
即给目标函数加一点东西。
现在,如果我们要最小化这个函数,那么为了最小化这个新的代价函数,我们要让\(θ3\)和\(θ4\)尽可能小。因为,如果你在原有代价函数的基础上加上1000乘以\(θ3\)这一项,那么这个新的代价函数将变得很大,所以,当我们最小化这个新的代价函数时,我们将使\(θ3\)的值接近于0,同样\(θ4\)的值也接近于0,就像我们忽略了这两个值一样。如果我们做到这一点(\(θ3\)和\(θ4\)接近0),那么我们将得到一个近似的二次函数。
更一般地:
\(L_2\)范数正则化:
\[min_w\sum_{i=1}^m(y_i-w^Tx_i)^2+\lambda ||w||_2^2 \] \[= min_w\sum_{i=1}^m(y_i-w^Tx_i)^2+\lambda\sqrt{\sum_{n=1}^nw_i^2}\]
(其中,m是数据个数,n是特征维度) 因此在正则化里,我们要做的事情,就是把减小我们的代价函数(例子中是线性回归的代价函数)所有的参数值,因为我们并不知道是哪一个或哪几个要去缩小。
因此,我们需要修改代价函数,在这后面添加一项,就像我们在方括号里的这项。当我们添加一个额外的正则化项的时候,我们收缩了每个参数。
\[ min_w\frac{1}{2m}[\sum_{i=1}^m(y_i-w^Tx_i)^2+\lambda\sqrt{\sum_{n=1}^nw_i^2}]\]