最近在做比赛,发现在工业上,很多分类问题的标签分布都是不平衡的。如参考文献标签倾斜修正方法记要所属,比如用分类器去判断x光片中的癌症,这是一个二元分类问题,由于癌症的比例是非常小的,比如0.001。那么,将这些样本放到大多数分类模型中训练,模型的表现会非常相似,将所有数据都预测为没有癌症,因为这样也可以得到99.999%的准确率。
常见的解决办法
参考文献解决真实世界问题:如何在不平衡类上使用机器学习?说,从不平衡数据中学习,是一项已被研究了 20 年之久的问题。它曾是许多论文、研讨会、特别议程的主题(一项最近的调查就有大约 220 个引用)。人们尝试了许多方法,但结果各不相同,所以至今没有得到明晰的答案。当数据科学家们第一次遇到这个问题,他们往往会问:「如果我的数据是不平衡的,我该怎么做?」而这一问题是没有固定答案的,就像你问「哪个学习算法是最好的」一样:答案取决于数据。
一般来说,有下面几种方法:
什么也不做
通过某些方法使得数据更加平衡:
- 对少数类进行过采样
- 对多数类进行欠采样
- 合成新的少数类
- 舍弃所有少数类,切换成一个异常检测框架。
在算法层面之上(或之后):
- 调整类的权重(错误分类成本)
- 调整决策阈值
- 使已有的算法对少数类更加敏感
- 构造一个在不平衡数据上表现更好的全新算法。
一种标签倾斜修正方法
参考文献Practical Lessons from Predicting Clicks on Ads at Facebook6.3指出,欠采样可以加快训练速度,提升模型表现。需要注意的是,就算数据被欠采样,其实也可以通过在欠采样空间中对预测结果进行修正。例如,在采样之前CTR只有0.1%,那么我们对负样本欠采样0.01,那么CTR就会变为10%。为了修正结果,使得CTR恢复到0.1%,我们可以通过公式: \[q=\frac{p}{p+(1-p)/w}\] 其中,\(p\)是欠采样空间下预测的概率, \(w\)是对负样本的采样率。
在这里我决定先复习一下先验概率、后验概率
先验概率、后验概率
先验概率是指事件尚未发生,对该事件发生的概率的估计,是在缺乏某个事情的情况下描述一个变量。 先验概率可以通过已知的关于事件本身的先验知识得到,蒙特卡洛方法也可以用于计算先验概率。 后验概率是指在事件已经发生的条件下,求该事件发生原因是由某个因素引起的可能性的大小,是考虑一个事件之后的条件概率。 后验概率可以基于 贝叶斯定理,通过先验概率乘以似然度,再归一化得到。具体来说,贝叶斯公式: \[P(h|D)=\frac{P(D|h)P(h)}{p(D)}\] 其中,\(P(h)\)为\(h\)的先验概率,\(P(h|D)\)为\(h\)的后验概率。 通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A(发生)的条件下的概率是不一样的;然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。贝叶斯公式的一个用途在于通过已知的三个概率函数推出第四个。
标签倾斜修正
参考文献标签倾斜修正方法记要通过理论推导来验证这个结论。 上参考文献作者提到,PRML的1.5.4节中介绍了一种标签倾斜修正的方法。
首先,你的模型必须是一个软分类器,即预测值为0到1之间的概率。假设输入向量x,预测标签\(C_k\),那么可以用条件概率表示,即计算\(p(C_k|x)\)的概率。根据贝叶斯公式,条件概率可以如下变化: \[p(C_k|x)=\frac{p(x|C_k)p(C_k)}{p(x)}\]
上面是没有做重采样时,得到概率。当做重采样时,只是改变了标签\(C_k\)的先验概率\(p(C_k)\),即将\(p(C_k)\)变为\(p'(C_k)\)(其实就是标签\(C_k\)的先验分布而已)。而\(p(x)\)是条件\(x\)发生的概率,不会变化。\(p(x|C_k)\)是后验概率,也不会变化。【问题,为什么不变?我感觉是因为特征是采样前的特征,因此这个没变】
因为是对负样本进行了抽样,假设对负样本抽样比例为\(w\),抽样后:
\[n'(0)=n(0)\times w,n'(1)=n(1)\]
易知: \[p(1)=\frac{n(1)}{n(1)+n(0)}=\frac{n'(1)}{n'(1)+n'(0)/ w}\] \[=\frac{p'}{p'+(1-p')/w}\] 其中,\(n(C_k)\)表示\(C_k\)的个数
我们推导出了先验概率\(p'(C_k)\)与\(p(C_k)\)的关系。那么,如果我们想修正\(p(C_k|x)\),则:
\[p(1|x) = \frac{p(x|1)p(1)}{p(x)} = \frac{p(x|1)p'(1)p(1)}{p(x)p'(1)}\] \[=p'(1|x)\frac{p(1)}{p'(1)}=p'(1|x)\frac{p}{p'}\]
而由之前的推导我们可知\(p=\frac{p'}{p'+(1-p')/w}\),代入得: \[p(1|x)=p'(1|x)\frac{p}{p'}=p'(1|x)\frac{\frac{p'}{p'+(1-p')/w}}{p'}\] \[=p'(1|x)\frac{1}{p'+(1-p')/w}\]
需要注意的是,\(p'(1|x)\)是预测出来的概率,\(p'\)是抽样之后正样本的比例,而在facebook的论文中,假设\(p'\approx p'(1|x)\)(也就是说,我们假设了预测集中,1出现的概率=预测出来的为1的概率。我的理解就是,我们完全信任了预测的结果),并记\(q=p'(1|x)\)则以上公式变为:
\[p(1|x)=\frac{q}{q+(1-q)/w}\]
【问题:在预测时,\(p'\)可不可以变为预测集的正样本比例\(p'\)】
结论
在欠采样中,假设对负样本采样率为\(w\),则直接将结果按照如下公式修正即可:
\[p=\frac{q}{q+(1-q)/w}\]
其中: - \(q\)是在欠采样之后,模型预测出来的概率。 - \(p\)是修正后的概率。
当w=0.1时,变换其实为:
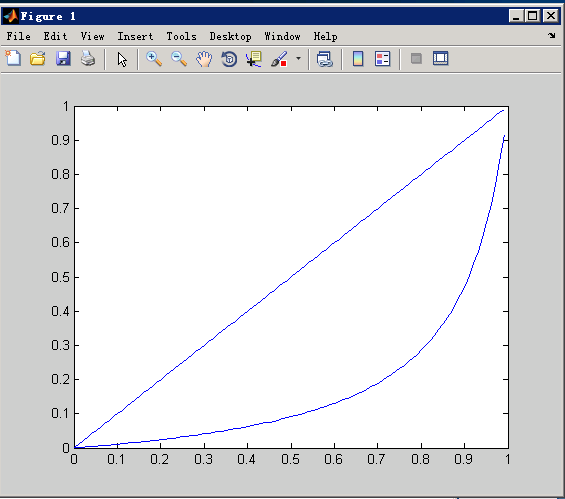
上面是y1=q(不做变换),下面是本变换y2。
而如果我们将y3=y1-y2绘出: 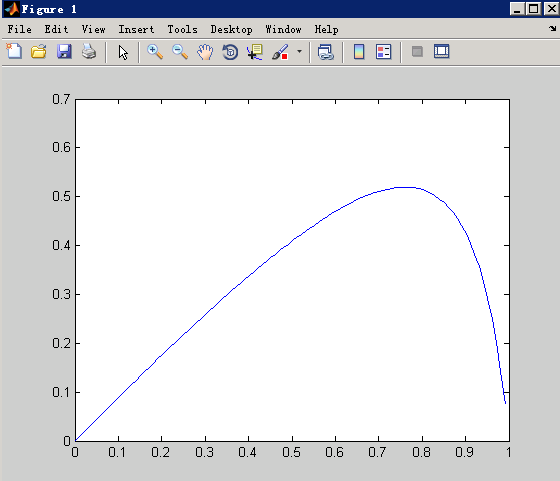
我们发现,概率大的压缩的小。 因为你负样本采样了之后,就是会预测的比实际的高一点,所以要给它压下去。
附上matlab代码: q=0.001:0.01:1; y1=1./(1+(1./q-1)./0.1); y2 = q; plot(q,y1); hold on; plot(q,y2); hold on; y3 = y2-y1; plot(q,y3)
小trick(有错,删掉)
如果在已知样本中,正样本的概率\(p\),那么:
\[p'(1)=\frac{n'(1)}{n'(1)+n'(0)}=\frac{n(1)}{n(1)+n(0)\times w}\] \[=\frac{1}{1+\frac{n(0)\times w}{n(1)}}=\frac{1}{1+\frac{p(0)\times w}{p(1)}}\] \[=\frac{p(1)}{p(1)+p(0)\times w}=\frac{p}{p+(1-p)\times w}\]
而因为: \[p(1|x)=p'(1|x)\frac{p}{p'}\]
代入得:
\[p(1|x)=p'(1|x)\frac{p}{\frac{p}{p+(1-p)\times w}}\] \[=p'(1|x)(p+(1-p)\times w)\]
这里的p是样本中,正样本的概率。 # 参考文献