简介

SVD(Singular Value Decomposition，奇异值分解)是对实数矩阵(甚至复数矩阵)的一种因式分解。
任意的一个矩阵都可以做SVD分解。相比SVD分解，和SVD相近的特征值分解只能应用于方阵。
SVD分解可用来解决非方阵不能计算逆矩阵的问题。

SVD定义

设一个\(m\times n\)的矩阵\(M\),它的SVD分解是： \[M=UΣV^*\] 其中： - \(U\)是一个\(m\times m\)的酉矩阵。(我的理解：酉矩阵是在复数空间上，类似正交矩阵的矩阵。它有很多不错的性质。可以在我上一篇博客里看到) - \(Σ\)是\(m\times n\)的矩形对角矩阵，并且在对角线上的元素都是非负实数\(σ_i\)，称为\(M\)的奇异值 - \(V^*\)是一个\(n\times n\)的酉矩阵，也是\(V\)的共轭转置矩阵。

SVD的原理

首先，我们对正交矩阵进行一些回顾。

正交矩阵回顾

从上一节我们知道，正交矩阵对应的变换是不会改变向量长度的。即，对于向量\((a,b)\)，正交矩阵\(U\)，变换后的向量\(U(a,b)\)的长度与\((a,b)\)是相等的。这个正交变换只是对\((a,b)\)做了旋转或者镜射等操作。

特征值分解——EVD

在讨论SVD之前，我们先讨论矩阵的特征值分解（EVD）。

回顾特征值分解，特征值分解是把一个n阶实对称矩阵分解为下面的形式： \[A=QΣQ^{-1}\] 其中： - \(Q\)是这个矩阵\(A\)的特征向量组成的矩阵，是一个正交矩阵 - \(Σ\)是一个对角阵，每个对角线上的元素就是一个特征值

此时假设有一个\(x\)向量，用\(A\)将这个向量\(x\)变换到\(A\)的列空间中，即： \[Ax=QΣQ^{-1}x=QΣQ^Tx=QΣ(Q^Tx)\] 1. 首先进行\(Q^Tx\)操作。\(Q\)和\(T^T\)都是正交阵，那么\(Q^T\)对\(x\)的变换是正交变换，它将\(x\)用新的坐标系，这个坐标系就是\(A\)的所有正交的特征向量构成的坐标系。我们如果将\(x\)用\(A\)的所有特征向量来表示的话，即表示为\(x=a_1x_1+a_2x_2+...+a_mx_m\)，则通过第一个变换，\((Q^Tx)=[a_1,a_2,...,a_m]'\),即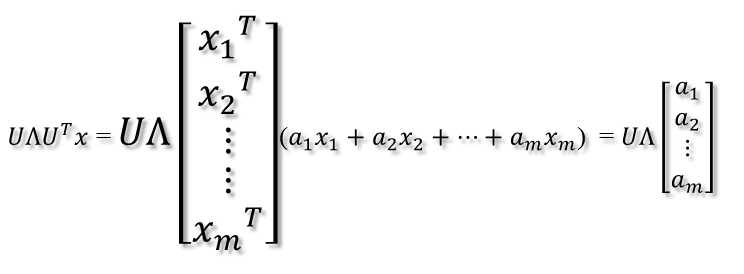 2. 紧接着，在新的坐标系表示下，由中间那个对角矩阵对新的向量坐标换，其结果就是将向量往各个轴方向拉伸或压缩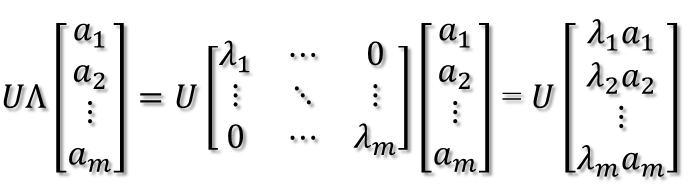：从上图可以看到，如果A不是满秩的话，那么就是说对角阵的对角线上元素存在0，这时候就会导致维度退化，这样就会使映射后的向量落入m维空间的子空间中。 3. 最后一个变换就是U对拉伸或压缩后的向量做变换，由于U和U'是互为逆矩阵，所以U变换是U'变换的逆变换。

因此，从对称阵的分解对应的映射分解来分析一个矩阵的变换特点是非常直观的。假设对称阵特征值全为1那么显然它就是单位阵，如果对称阵的特征值有个别是0其他全是1，那么它就是一个正交投影矩阵，它将m维向量投影到它的列空间中。

奇异值分解--SVD

上面的矩阵\(A\)要求必须是n阶实对称的。那么对于任意的\(M\times N\)矩阵，能否找到一个相似的变换呢？这就是SVD分解的精髓所在。

在上面的特征值分解中，我们能找到一个变换\(A\)，将一组正交基映射到另一组正交基。

我们假设存在\(M \times N\)的矩阵\(A\)。现在我们的目标是，在n维空间中找到一组正交基\[{v_1,v_2,...,v_n}\]，使得经过A变换后还是正交的。
那么\(A\)矩阵就将这组基映射为：\[{Av_1,Av_2,...,Av_n}\]
如果要使得它们两两正交，即：\[Av_i\cdot Av_j = (Av_i)^TAv_j=v_i^TA^TAv_j=0\]
根据假设，存在\[v_i^Tv_j=v_i\cdot v_j = 0\]
所以如果正交基v选择为A'A的特征向量的话，由于A'A是对称阵，v之间两两正交，那么\[v_i^TA^TAv_j=v_i^T\lambda _jv_j=0\]，这样就找到了正交基映射后还是正交基了。
将映射后的正交基单位化，\[u_i = \frac{Av_i}{|Av_i|}=\frac{1}{\sqrt{\lambda_i}}Av_i\] 其中\(u_i\)是映射后的正交基，\(v_i\)是映射前的正交基。
由此可得，\[Av_i=u_i\alpha_i(奇异值)=\sqrt{\lambda_i},0\leq i \leq k,k=Rank(A)\]

这样我们就证明了，这个变换是存在的。

接下来，我们将向量组\({u_1,u_2,...,u_k}\)扩充为\(R^m\)中的标准正交基\(u_1,u_2,...,u_r,...,u_m\)，则： \[AV=A(v_1,v_2,...,v_n)=(Av_1,Av_2,...,Av_k,0,0,...,0)\] 而由之前的推导我们知道，\(Av_i=u_i\alpha_i(奇异值)\)，因此上式变为 \[AV=(u_1\alpha_1,u_2\alpha_2,...,u_k\alpha_k,0,0,...,0)=UΣ\]

即： \[A=UΣV^T\]

这就表明任意的矩阵\(A\)是可以分解成三个矩阵。\(V\)表示了原始域的标准正交基，\(U\)表示经过\(A\)变换后的co-domain的标准正交基，\(Σ\)表示了\(V\)中的向量与\(U\)中相对应向量之间的关系。

其中： - \(A是m\times n维度\) - \(U叫左奇异向量，是m\times m维的正交矩阵\) - \(Σ叫右奇异向量，是n\times n维的对角矩阵，但实际上只有左上角的k阶非零\),即: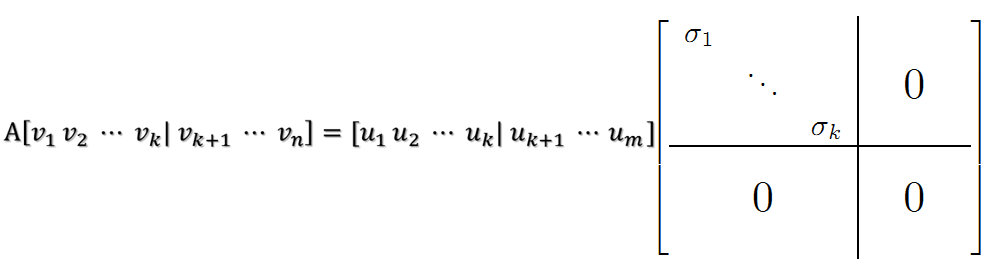

从大小上来看：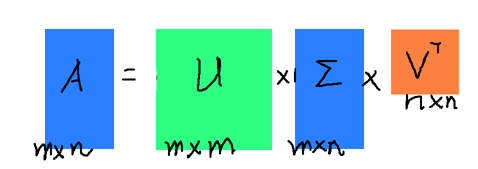

即：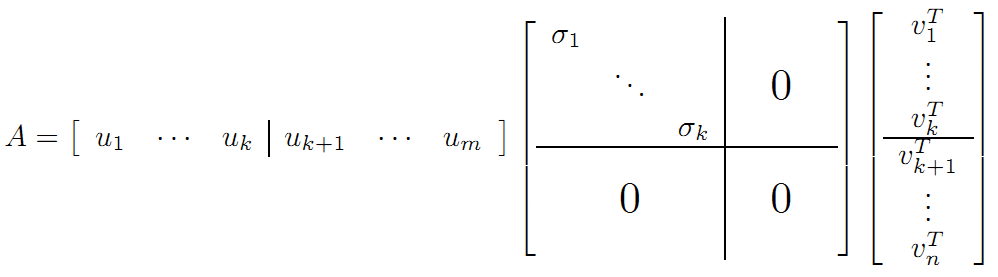

特征值分解与奇异值分解

参考文献机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用提到，奇异值和特征值可以对应起来。

部分奇异值分解

在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解： \[A_{m\times n}\approx U_{m\times r}Σ_{r_\times r}V^T_{r\times n}\] r是一个远小于m、n的数，这样矩阵的乘法看起来像是下面的样子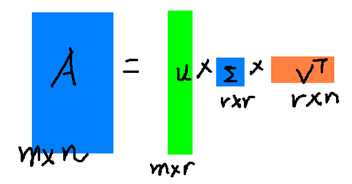：右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。

小例子

接下来我们给出一个用python的SVD分解小例子。


#coding=utf-8
# 首先做一些数据声明
from sklearn.decomposition import TruncatedSVD
from matplotlib import pyplot as plt
from numpy import random
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd
fig = plt.figure()
ax = Axes3D(fig)
ax=plt.subplot(111,projection='3d')
ax.set_zlabel('Z') #坐标轴
ax.set_ylabel('Y')
ax.set_xlabel('X')
X = np.arange(0, 4, 0.125) + 0.2 * random.randn(32)
Y = np.arange(0, 4, 0.125) + 0.2 * random.randn(32)
Z = np.arange(0, 4, 0.125) + 0.2 * random.randn(32)
# 数据是3维×32维
data = [[x, y, z] for x, y, z in zip(X, Y, Z)]

# 分解，n_components是主元素个数，也就是维度
svd = TruncatedSVD(n_components=2, algorithm="arpack", n_iter=1000)
transformed_data = svd.fit_transform(data)
# 还原
data_inverse = svd.inverse_transform(transformed_data)

#画图
X_ = [x[0] for x in data_inverse]
Y_ = [y[1] for y in data_inverse]
Z_ = [z[2] for z in data_inverse]
ax.scatter(X, Y, Z, c='r')#原始数据是红色
ax.scatter(X_, Y_, Z_, c='b')#分解后的数据是蓝色
plt.savefig("svd.png")
plt.show()
print svd.explained_variance_ratio_
'''

当降到二维，再还原时，我们看到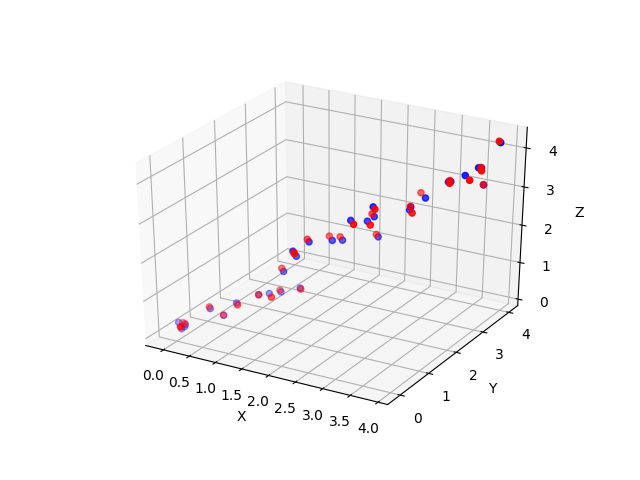：降到一维，再还原，我们看到：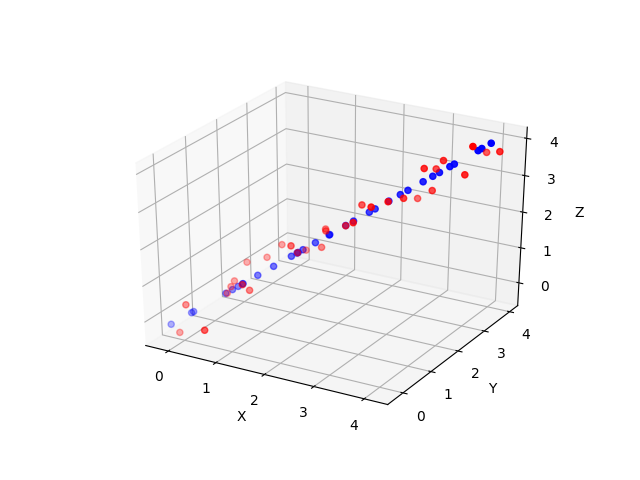

SVD与潜在语义索引

\[A=UΣV^T\]

吴军老师在矩阵计算与文本处理中的分类问题中谈到：三个矩阵有非常清楚的物理含义。 - \(U\)中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。 - \(V^T\)中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。 - 因此，我们只要对关联矩阵\(A\)进行一次奇异值分解，我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。

参考文献机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用给出了一个理解这句话的例子，此处不再阐述。

我在做比赛的过程中，曾尝试过用SVD分解做APP特征，来描述APP之间的相似性特征。但效果不佳。推测原因是维度过低（几百万维压到了20维）。项目在这里

但这里我还是打算好好看看。万一以后用到呢？

参考文献SVD在推荐系统中的应用以经典的电影评分问题为例，讲述了整个过程。参考文献SVD在推荐系统中的应用用matlab进行了详细的过程复现。

我的理解： SVD分解 SVD分解是：\[A_{m\times n}=U_{m\times m}Σ_{m\times n}V^T_{n\times n}\] 其中： - \(Σ_{m\times n}\)是一个对角阵。 - \(U_{m\times m}\)表示行间元素（一般是用户）的相似度 - \(V^T_{n\times n}\)表示列间元素（一般是商品）的相似度根据好友张思遥的理解，是通过数学的方法，来将行和列的拆开，放在两个矩阵里。降维根据PCA理论（强烈建议看斯坦福大学安德鲁老师的机器学习课程，这里有前辈的笔记斯坦福ML公开课笔记14——主成分分析，我们可以取前\(r\)维来对矩阵进行近似表示： \[A_{m\times n}\approx U_{m\times r}Σ_{m\times n}V^T_{r\times n}\]

# 基本的SVD，但这个很难得到U
svd = TruncatedSVD(n_components=5, n_iter=7, random_state=42)
A = svd.fit(install_data)

# 快速SVD分解
U, Sigma, VT = randomized_svd(install_data,n_components=10) # n_components代表降维之后的维度，即U 为 m × components 维
U = DataFrame(U)

项目代码

SVD项目代码