思想
希尔排序的实质是分组插入排序,又称缩小增量排序。
该方法的基本思想是: 1. 先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的),对这些子序列分别进行直接插入排序 2. 依次缩减增量再进行排序 3. 待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
例子
现在我们要将这样一个数组排序,一共有10个元素

- 第一次 增量 gap = 10/2 = 5
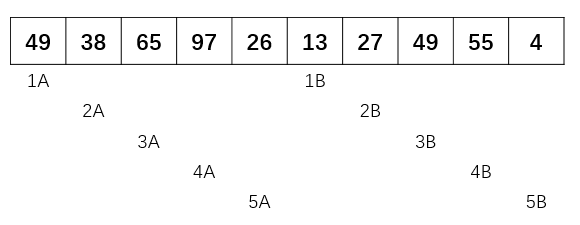
整个数组被分成了5个子数组,分别是[49,13],[38,27],[65,49],[97,55],[26,4] 然后对这五个子数组进行插入排序,得到下面结果

- 第二次 增量 gap = 5/2 = 2
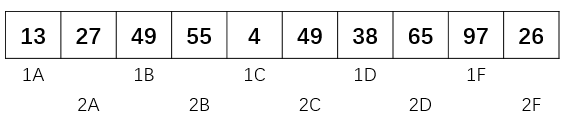
这次我们把整个数组分成了两个子数组,分别是[13,49,4,38,97],[27,55,49,65,26] 对这个两个子数组排序,结果如下: 
- 第三次 增量 gap = 2/2 = 1 此时整个数组已经接近有序,对整个数组进行全排列

最终得到数组有序

代码
1 | //希尔排序 |
优化
白话经典算法系列原文是这么说的 >很明显,上面的shellsort1代码虽然对直观的理解希尔排序有帮助,但代码量太大了,不够简洁清晰。因此进行下改进和优化,以第二次排序为例,原来是每次从1A到1E,从2A到2E,可以改成从1B开始,先和1A比较,然后取2B与2A比较,再取1C与前面自己组内的数据比较…….。这种每次从数组第gap个元素开始,每个元素与自己组内的数据进行直接插入排序显然也是正确的。
我理解了一下,思路就是把在序列中提取子序列的过程简化了,我们可以从第gap个元素开始,向后遍历到序列末尾,可以个元素都跟其所在的子序列中位于它前面的数字做插入排序,最终就会得到一个有序数列了~
画个图表示一下吧,还是刚才那个序列,比如说此时进行到第二次排序了,gap=2的情况:
从a[2]开始遍历,此时a[2]所在的子序列为[a[0],a[2],a[4],a[6],a[8]],需要将a[2]和位于它前面的a[0]比较,插入到合适的位置:

指针后移一位, 同上此时a[3]所在的子序列为[a[1],a[3],a[5],a[7],a[9]],需要将a[3]和位于它前面的a[1]比较,插入合适的位置:

接下来指针指向a[4],此时需要将a[4]和位于它前面的a[2]、a[0]比较,插入合适的位置:
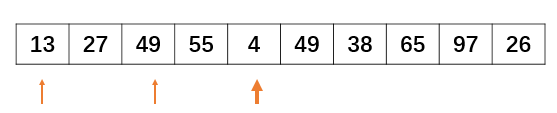
下面重复上面的步骤:
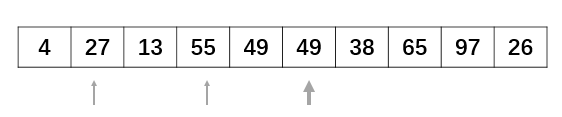
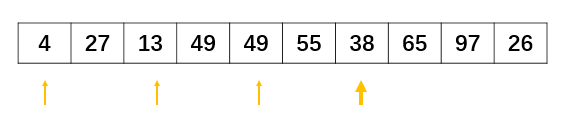
此处省略剩余步骤.....最终可以将数组排列至有序状态
现在可以上代码了~ 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//希尔排序
void HillSort(int a[], int len) {
int delta = len/2;
while (delta > 0) {
for (int i = delta; i < len; i++) {//遍历
//对该元素子前面的子数组进行插入排序
int temp = a[i];
int jj = i - delta;
while ((jj >=0)&&(a[jj]>temp)){
swap(a[jj], a[jj+delta]);
jj -= delta;
}
}
delta = delta / 2;
}
}