甲乙小朋友的房子

甲乙小朋友很笨，但甲乙小朋友不会放弃

0%

归并排序

发表于 更新于 分类于

思路

分治法 将数组分成A、B两组，如果这二组组内的数据都是有序的，那么就可以很方便的将这二组数据进行排序。如何让这二组组内数据有序了？

可以将A，B组各自再分成二组。依次类推，当分出来的小组只有一个数据时，可以认为这个小组组内已经达到了有序，然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列，再合并数列就完成了归并排序。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//将两个有序数组合并成一个有序数组
void merge(int a[], int begin,int mid,int end,int b[]) {
    int i = begin;
    int j = mid + 1;
    int k = 0;
    while ((i <= mid) && (j <= end)) {
        if (a[i] < a[j]) {
            b[k] = a[i];
            k++;
            i++;
        }
        else{
            b[k] = a[j];
            k++;
            j++;
        }
    }
    while (i<=mid){
        b[k] = a[i];
        k++;
        i++;
    }
    while (j <= end){
        b[k] = a[j];
        k++;
        j++;
    }
    for (int i = 0; i < k; i++){
        a[begin + i] = b[i];
    }
}
//归并排序
void MergeSort(int a[], int begin,int end,int b[]) {
    if (begin < end) {
        int mid = (begin + end) / 2;
        MergeSort(a, begin, mid, b);
        MergeSort(a, mid + 1, end, b);
        merge(a, begin, mid, end, b);
    }
}

时间复杂度

由于归并排序是先将数组分成两部分，将两部分分别排序后，再合并。假设n个元素排序的时间是T(n)，而两部分分别排序的时间是T(n/2)，合并的复杂度是cn；因此：

\[T(n) = 2T(n/2) + cn\]

再解释一下\(T(n) = 2T(n/2) + cn\) 这个东西，$ 2T(n/2)$ 是下一层带来的代价，\(cn\) 是本层带来的代价。因此我们画一颗递归树，树的【每层表示本层所消耗的代价】，如下图所示：

  • 第一行cn表示当前层消耗的代价
  • 第二行两个T(n/2)代表下一层消耗的代价

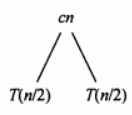
将这个递归树再往下拓展一层，我们得到：

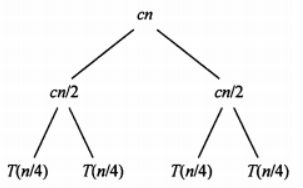
我们再进行扩展：

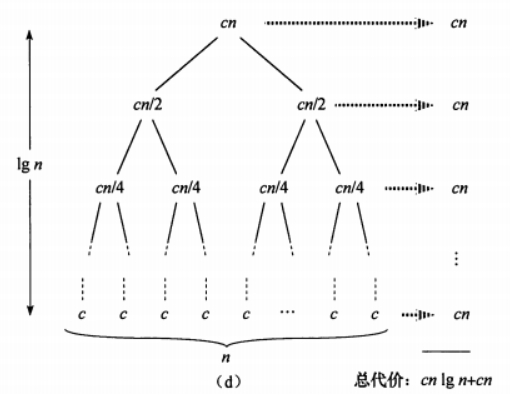
我们看到，完全扩展了的递归树具有\(logn + 1\) 层，其中每层的代价都是\(cn\) 。因此总的代价为【每一层的代价之和】：

\[cn (log n + 1) = cnlogn + cn = O(nlogn)\]

  • 最坏情况\(O(n\log(n))\)
  • 平均情况\(O(n\log(n))\)