LR的梯度下降

在LR中，我们想要得到z=wx+b，并且这个z在样本上，损失函数L(a,y)最小。那么，我们可以不断地改变w和b，找到一个合适的w和b，达到我们上述的目的。

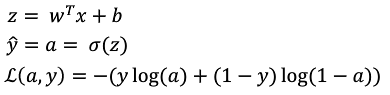
如何改变w和b，能更快地得到最优的w和b呢？那么我们就要使用梯度下降法。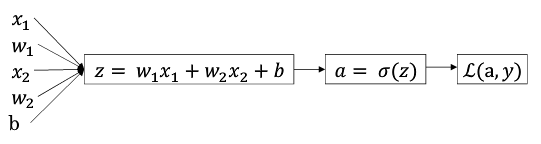

上图中，从左到右的计算过程就是前向传播法。

一般来说，我们都用后向传播法来计算这个过程：

在单个样本中，想要计算$L(a,y)$的导数: 1. 先向前一步，计算损失函数$L(a,y)$关于$a$的导数$da = \frac{dL(a,y)}{da} = -\frac{y}{a} + \frac{1-y}{1-a}$。 2. 再向前一步，计算$dz = \frac{dL}{dz} = a - y$ 3. 再向前一步，计算$dw = \frac{dL}{dw} = ...=x(a-y), db = ...=a-y$ 4. 用 $ w = w - dw,b = b - db$

在m个训练集中， $J(w,b) = \frac{1}{m} \sum{_i^m L(a^{(i)},y^{(i)})}$ 那么： $\frac{d(J(w,b))}{w1} = \frac{1}{m}\sum_i^m\frac{d(L(w^{(i)},y^{(i)}))}{w_i}$

也就是说，m个训练样本的损失函数的导数 = 每个训练样本损失函数导数的均值

伪代码：

J = 0; dw1 = 0; dw2 = 0 ; db = 0;
for i = 1 to m :
    z = w1x1[i] + w2x2[i] + b ;
    y = sigmod(z) ;
    a = get(i) ;
    J += ylog(a) + (1-y)log(1-a);
    dz = a - y; # 先算dz
    dw1+= x1dz; # 后算dw,db
    dw2 += x2dz;
    db+= dz;
J/= m;
dw1 /= m;
dw2 /= m;
db /= m;

此时就已经得到了全部样本的dw1,dw2,db,J

然后应用梯度下降：

w1 = w1 - sdw1
w2 = w2 - sdw2
b = b - sb

其中，s是步长。

向量化

一般来说，for循环是很不好的。可以使用向量化来摆脱for循环，加速运算。接下来我们来讲一讲向量化。

一般来说，如果我们想计算$z = w^T x + b$,其中，w和x都是一个n维的列向量。在非向量化实现中，我们会用：

z = 0;
for i in range(n):
    z += w[i]*x[i];
z += b ;

在向量化（例如numpy中），我们用：

z = np.dot(w,x) + b

向量运算非常快（主要原因是并行运算）。因此我们尽量将loop运算转换为向量运算。

向量化的LR

x是m维向量

import numpy as np
J = 0; dw1 = 0; dw2 = 0 ; db = 0;
z = np.dot(w.T,x) + b; # m维列向量
y = sigmod(z) ;# m维列向量
a = label;# m维列向量
J = np.dot(y.T,log(a)) + np.dot((1-y).T,log(1-a));
J/= m;
dz = a - y; # 先算dz
dw1 = np.dot(x1.T,dz) /m ; # 后算dw,db
dw2 = np.dot(x2.T,dz) /m ;
db= np.sum(dz) /m ;

然后应用梯度下降：

w1 = w1 - sdw1
w2 = w2 - sdw2
b = b - sb

总结

这一节主要讲了我们如何将梯度下降法应用到LR中，以及强调了Nuppy。应该只是为了后续的学习做一些准备。

一定一定要看这个作业通过神经网络mindset实现简单的Logistic Regression

甲乙小朋友的房子

深度学习算法-引言-LR的梯度下降法

LR的梯度下降

向量化

向量化的LR

总结