之前的博客中简单介绍了Learning to Rank的基本原理，也讲到了Learning to Rank的几类常用的方法：pointwise，pairwise，listwise。这篇博客就pairwise中的RankSVM、GBRank和LambdaRank做简要介绍。
RankSVM是2000年提出的；GBRank是2007年提出的；LambdaMART是2008年提出的。因此我们按照提出顺序来讲解这三种算法。
引言
机器学习一般都是解决分类问题。而在Rank中我们遇到的是排序问题。那么如何将排序问题转化为分类问题成了当下的关键。
如何将排序问题转化为分类问题？
对于一个query-doc pair（检索-文档结果对），我们可以将其用一个feature vector表示：x。而排序函数为f(x)，我们根据f(x)的大小来决定哪个doc排在前面，哪个doc排在后面。即如果f(xi) > f(xj)，则xi应该排在xj的前面，反之亦然。可以用下面的公式表示：
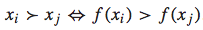
理论上，f(x)可以是任意函数，为了简单起见，我们假设其为线性函数：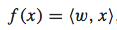 
如果这个排序函数f(x)是一个线性函数，那么我们便可以将一个排序问题转化为一个二元分类问题。理由如下： 首先，对于任意两个feature vector xi和 xj，在f(x)是线性函数的前提下，下面的关系都是存在的： 
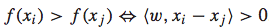然后，便可以对xi和 xj的差值向量考虑二元分类问题。特别地，我们可以对其赋值一个label：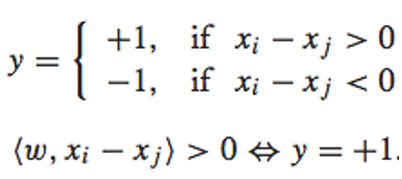 
有一个很好的例子说明了如何将排序问题转化为分类问题，在L2R的笔记中已提到过，此处不再多加阐述。
将排序问题转化为分类问题之后, 我们就可以使用常用的机器学习方法解决该问题。
RankSVM
RankSVM的基本思想是，将排序问题转化为pairwise的分类问题，然后使用SVM分类模型进行学习并求解。Ranking SVM使用SVM来进行分类: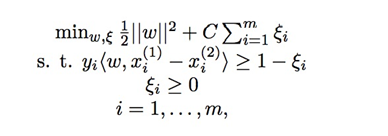 
其中w为参数向量, x为文档的特征,y为文档对之间的相对相关性, ξ为松弛变量。
对这个公式，知乎上有一个很好的解释： 之前svm为实现软间隔最大化，约束条件里有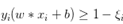
。而rank-svm是典型的pairwise方法，考虑两个有偏序关系的文档对，训练样本是xi(1)-xi(2)，所以要把约束条件改成
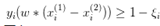，由于相减不再需要偏置b。而优化问题中的目标函数和其他约束项不变。
使用Clikthrough数据作为训练数据
T. Joachims提出了一种非常巧妙的方法, 来使用Clickthrough数据作为Ranking SVM的训练数据。
假设给定一个查询"Support Vector Machine", 搜索引擎的返回结果为 
其中1, 3, 7三个结果被用户点击过, 其他的则没有。因为返回的结果本身是有序的, 用户更倾向于点击排在前面的结果, 所以用户的点击行为本身是有偏(Bias)的。为了从有偏的点击数据中获得文档的相关信息, 我们认为: 如果一个用户点击了a而没有点击b, 但是b在排序结果中的位置高于a, 则a>b。 所以上面的用户点击行为意味着: 3>2, 7>2, 7>4, 7>5, 7>6。
Ranking SVM的开源实现
Joachims的主页上有Ranking SVM的开源实现。
数据的格式与LIBSVM的输入格式比较相似, 第一列代表文档的相关性, 值越大代表越相关, 第二列代表查询, 后面的代表特征: qid:1 1:1 2:1 3:0 4:0.2 5:0 # 1A qid:1 1:0 2:0 3:1 4:0.1 5:1 # 1B qid:1 1:0 2:1 3:0 4:0.4 5:0 # 1C qid:1 1:0 2:0 3:1 4:0.3 5:0 # 1D
qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2A
qid:2 1:1 2:0 3:1 4:0.4 5:0 # 2B qid:2 1:0 2:0 3:1 4:0.1 5:0 # 2C qid:2 1:0 2:0 3:1 4:0.2 5:0 # 2D
qid:3 1:0 2:0 3:1 4:0.1 5:1 # 3A qid:3 1:1 2:1 3:0 4:0.3 5:0 # 3B qid:3 1:1 2:0 3:0 4:0.4 5:1 # 3C qid:3 1:0 2:1 3:1 4:0.5 5:0 # 3D
GBRank
参考文献GBRank:一种基于回归的学习排序算法 对GBRank做出了较好的解释。原论文是[A Regression Framework for Learning Ranking Functions Using Relative Relevance Judgments]。下面对这个博客和论文进行摘录和整理。
算法原理
一般来说在搜索引擎里面，相关性越高的越应该排在前面。现在 query-doc 的特征使用向量x或者y表示，假设现在有一个文档对<xi,yi>，当xi排在yi前面时，我们使用xi>yi来表示。我们含顺序的 pair 对用如下集合表示(也就是真的xi真的排在yi前面):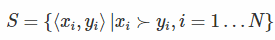 
现假设学习的排序函数为h，我们希望当h(xi)>h(yi)时，满足xi>yi的数量越多越好。那么如何来评价这个h到底好不好呢，那么我们可以定义h的风险函数为: 
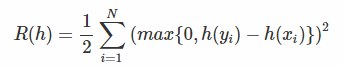对于这个风险函数，我们可以做如下解释。我们的目标是：对于集合S中的某个文档对<xi,yi>来说，h要符合我们之前的设定，也就是：
当h(xi)>h(yi)时，h是正确的，不造成损失； 当h(xi)<h(yi)时，h是不符合预期的，会造成损失，并且损失的大小成残差的平方级别；
将R(h)与每个 pair 对<xi,yi>的cost画成图可表示为：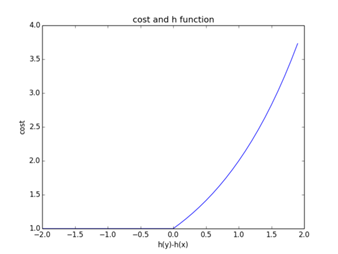 
上述风险函数直接优化比较困难，这里一个巧妙的解决方案：也就是首先固定h(xi)或者h(yi)当中其中的一个，然后再通过回归的方式来解决问题。 为了避免优化函数h是一个常量，我们对风险函数加入一个平滑项τ(0<τ≤10)：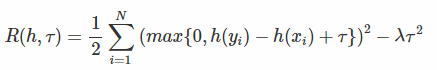 
其实加上了这个平滑项之后，一来可以防止h变为常数，二来还对损失函数给了更严格的条件：如果希望xi>yi，就得有h(xi)>h(yi)+τ，也就是更为严格了。
接下来我们用Functional Gradient Descent法来求解h.
参考文献Learning to Rank算法介绍：GBRank对这个求解方法做了扼要的介绍：
在GBDT中，Functional Gradient Descent的使用为：将需要求解的F(x)表示成一个additive model，即将一个函数分解为若干个小函数的加和形式，而这每个小函数的产生过程是串行生成的，即每个小函数都是在拟合 loss function在已有的F(x)上的梯度方向（由于训练数据是有限个数的，所以F(x)是离散值的向量，而此梯度方向也表示成一个离散值的向量），然后将拟合的结果函数进一步更新到F(x)中，形成一个新的F(x)。
- 将h(xi)和h(xi)作为未知数。梯度下降使得R最小，来求得这些未知数。
- 对R计算h的负梯度：
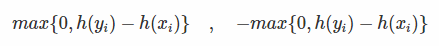
- 当pair对<xi,yi>符合条件时，上述梯度为0；反之，他们对应的梯度为：
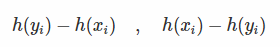
- 接下来，还需要知道如何将梯度作用到h的更新上。通过设定xi的目标值为h(yi)+τ。yi的目标值为h(xi)−τ（这一步我的理解就是首先固定x/y中的某一个，然后去计算另一个）。因此在每轮迭代中，当h不满足<xi,yi>会产生一组数据：
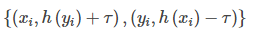
我们需要拟合本轮产生的所有负例。
下面形式化本算法： 
可以看到step3里面每轮都拟合误判的结果，在迭代中这个集合会越来越小。还有一种做法是将曾经误判的集合维持在训练集中，那么训练集就会始终增长。在这个步骤中使用GBDT模型进行回归预测，当然其他的回归方法也可以使用。
LambdaMART
在learn to rank的成长过程中，2000提出了SVMRank，2006年提出GBrank，2008年提出lambdaMART。看了几个比较大的框架，我发现现在市面上最常见的learn to rank算法就是LambdaMART了。接下来先介绍一下LambdaMART的原理，然后再介绍xgboost中是怎么写的LambdaMart。
LambdaMart的原理
这一小节主要参考资料LambdaMART 不太简短之介绍
Pointwise和Pairwise类型的LTR算法，将排序问题转化为回归、分类或者有序分类问题。Listwise 类型的 LTR 算法则另辟蹊径，将用户查询（Query）所得的结果作为整体，作为训练用的实例（Instance）。
LambdaMART 是一种 Listwise 类型的 LTR 算法，它基于 LambdaRank 算法和 MART(Multiple Additive Regression Tree)算法，将搜索引擎结果排序问题转化为回归决策树问题。MART实际就是梯度提升决策树（GBDT, Gradient Boosting Decision Tree）算法。GBDT 的核心思想是在不断的迭代中，新一轮迭代产生的回归决策树模型拟合损失函数的梯度，最终将所有的回归决策树叠加得到最终的模型。LambdaMART使用一个特殊的 Lambda 值来代替上述梯度，也就是将LambdaRank算法与MART算法加和起来。考虑到LambdaRank是基于RankNet算法的，所以在搞清楚LambdaMART算法之前，我们首先需要了解 MART、RankNet 和 LambdaRank 是怎么回事。
MART其实也是GBDT。此处对GBDT不再做过多的介绍。值得一提的是，MART并不对损失函数的形式做具体规定。实际上，损失函数几乎只需要满足可导这一条件就可以了。这一点非常重要，意味着我们可以把任何合理的可导函数安插在 MART 模型中。LambdaMART 就是用一个 λ 值代替了损失函数的梯度，将 λ和 MART 结合起来罢了。
LambdaMART是怎么来的
Lambda 的设计，最早是由 LambdaRank 从 RankNet 继承而来。因此，我们先要从 RankNet 讲起。 后记：其实这些文章都是到处整理得来，远不及直接看论文的好。如果有兴趣的话，可以读一读微软整理的这篇论文https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/MSR-TR-2010-82.pdf
RankNet的创新
Ranking常见的评价指标都无法求梯度，因此没法直接对评价指标做梯度下降。
RankNet 的创新之处在于，它将不适宜用梯度下降求解的Ranking问题，转化为对概率的交叉熵损失函数的优化问题，从而适用梯度下降方法。
RankNet的终极目标是得到一个带参的算分函数s = f(x;w)
参考文献机器学习---RankNet.md](https://github.com/MangoLiu/mangoliu.github.io/blob/master/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0---RankNet.md)给了一个非常好的例子：那么如何通过pair来训练，并最终作用到针对point的算分函数上，请看下面的简单例子。假设有以下同一个query下的4个文档，并且有3个特征维度，并对它们进行了人工打分，我们就利用它们来训练model。
point 特征f1 特征f2 特征f3 label
文档doc1 3 2 1 3(很好)
文档doc2 1 2 1 2（好）
文档doc3 1 1 2 1（一般）
文档doc4 1 0 3 0（不好） 于是，根据这个算分函数，我们可以根据特征来计算文档xi和xj的得分si和sj： Si = f(xi;w),sj = f(xj,w)
我们并不知道每个特征维度的具体权值w[i]。但我们感觉到要训练出这样的结果，就是使label得分比较高的样本得分尽量大，让label低的样本得分尽量小。 即本例中，我们应该让f(doc1)得分尽量大，f(doc4)得分尽量小。其实也就是f(doc1)-f(doc4)的结果尽量大，因为这个分差实际就包含了前者尽量大后者尽量小的含义。并且之前那个常量b通过作差后，不见了。 这样两两文档即可组成一个文档对，我们把前者好于后者的成为正向文档对；反之称之为负向文档对。正向对表示前者好于后者，负向对表示后者劣于前者。其实表述的是同样的意义。因此，我们只需要正向的对就好了。因为负向对不能再额外提供有意义的信息了。那么我们提取出上面的正向对：
Pair 作差 特征f1 特征f2 特征f3
P12 (doc1-doc2) 2 0 0
P13 (doc1-doc3) 2 1 -1
P14 (doc1-doc4) 2 2 -2
P23 (doc2-doc3) 0 1 -1
P24 (doc2-doc4) 0 2 -2
P34 (doc3-doc4) 0 1 -1需要注意的是，这里的特征也进行了相减！
我们再引入一个文档对概率，表示文档i好于文档j的概率。我们将它称为两者的偏序概率：(这个东西我理解为是将偏序关系转化为概率的函数，类似于lr里面的sigmod函数)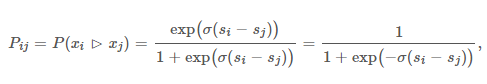 
那么，现在这个问题就转化成了使所有正向对的概率和最大。我们现在已经知道了目标函数，那么接下来就需要一个损失函数来将这个目标函数最优化。 再将以上的交叉熵定义为损失函数：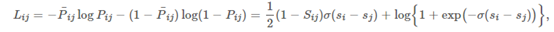 
然后对这个损失函数进行梯度下降： 
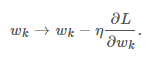在以上的方法中，我们将偏序关系转化为目标函数，然后再定义目标函数的损失函数，再通过梯度下降法求参数使得损失函数最小，得到目标函数。那么我们能不能直接定义梯度呢？
LambdaRank
参考文献Learning To Rank之LambdaMART的前世今生对下面这个图有非常详细的解释。此处对一些重点内容进行摘录。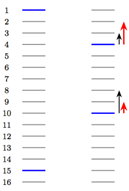 
如图所示，每个线条表示文档，蓝色表示相关文档，灰色表示不相关文档。 RankNet以pairwise error的方式计算cost，左图的cost为13，右图通过把第一个相关文档下调3个位置，第二个文档上条5个位置，将cost降为11，但是像NDCG或者ERR等评价指标只关注top k个结果的排序，在优化过程中下调前面相关文档的位置不是我们想要得到的结果。图 1右图左边黑色的箭头表示RankNet下一轮的调序方向和强度，但我们真正需要的是右边红色箭头代表的方向和强度，即更关注靠前位置的相关文档的排序位置的提升。
LambdaRank正是基于这个思想演化而来，其中Lambda指的就是红色箭头，代表下一次迭代优化的方向和强度，也就是梯度。 受LambdaNet的启发，LambdaRank对RankNet的梯度做因式分解：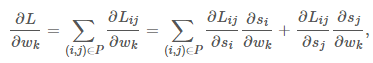 
注意有下面对称性 
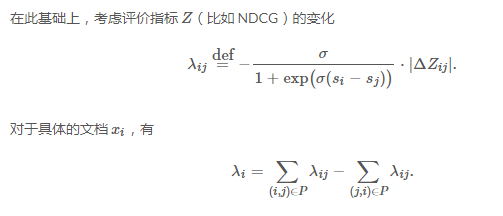也就是说：每条文档移动的方向和趋势取决于其他所有与之 label 不同的文档。 现在回过头来看，看看我们做了些什么？ - 分析了梯度的物理意义； - 绕开损失函数，直接定义梯度。 当然，我们可以反推一下 LambdaRank 的损失函数：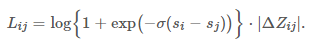 
LambdaMART 现在的情况变成了这样： - MART 是一个框架，缺一个「梯度」； - LambdaRank 定义了一个「梯度」。 于是，就有了 LambdaMART： 
Xgboost中的Learning to rank
为了后续方便后续小伙伴们的使用，我将官方文档xgboost的learning to rank文档进行扼要的翻译，并在此贴出。 Xgboost的rank模型是基于lambdaRank的。 XGBoost支持以ranking为目标的学习。在ranking的情况下，数据集一般都需要被格式化为group input： 在ranking中，数据是根据不同的真实场景被分为groups的。例如，在学习web pages的rank场景下，rank page数据是根据不同的queries分到各groups的。
数据形式 基本数据形式train.txt Xgboost接受像libSVM格式数据，例如：
1 101:1.2 102:0.03
0 1:2.1 10001:300 10002:400
0 0:1.3 1:0.3
1 0:0.01 1:0.3
0 0:0.2 1:0.3每行表示：
label 特征1索引:值 特征2索引:值groups索引文件train.txt.group 除了group input format,XGboost需要一个索引group信息的文件，索引文件train.txt.group格式如下：
2
3这意味着，数据集包含5个实例，前两个是一个group，后三个是一个group。
实例权重文件train.txt.weight
XGboost还支持每个实例的权重调整，数据格式如下：
1
0.5
0.5
1
0.5初始margin文件train.txt.base_margin
XGBoost还可以支持每个实例的初始化margin prediction.例如我们对train.txt可以有一个initial margin file:
-0.4
1.0
3.4XGBoost will take these values as initial margin prediction and boost from that. An important note about base_margin is that it should be margin prediction before transformation, so if you are doing logistic loss, you will need to put in value before logistic transformation. If you are using XGBoost predictor, use pred_margin=1 to output margin values.
使用Demo:
xgboost的pairwiseRank实现
****如何构造pair对？ xgboost/src/objective/rank_obj.cc,75行开始构造pair对。如上理论所说，每条文档移动的方向和趋势取决于其他所有与之 label 不同的文档。因此我们只需要构造不同label的“正向文档对”。其方法主要为:遍历所有的样本，从与本样本label不同的其他label桶中，任意取一个样本，构造成正样本； 如何定义梯度？ xgboost/src/objective/rank_obj.cc中，写到了它是使用lambdaWeight. 然后将梯度和文档对输入GBDT训练即可。 ****输出是什么？** 根据labdaMart原理，输出是模型对每个文档的打分。
# 参考文献
Learning to Rank之Ranking SVM 简介 GBRank:一种基于回归的学习排序算法 gbRank & logsitcRank自顶向下