在说钢条切割问题之前,我们先说说动态规划。
动态规划——Dynamic programming(这个词指表格):通过组合子问题的解求解原问题。
与分治法对比:
- 相同点:都是通过子问题组合求解原问题
- 不同点:分治法将问题划分为不相交的子问题,求解再合并。动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题,此时如果用分治法就会出现重复计算求解。为了避免重复动态规划对子问题只求解一次,将其保存在表格中,从而无需每求解一个子子问题时重复计算。
求解步骤
- 刻画最优解的结构特征
- 递归定义最优解的值
- 计算最优解的值,通常采用自底向上的方法(可能需要同时维护一些额外信息)
- 利用计算出的信息构造最优解(不是必须)
钢条切割
Serling公司购买一根长钢管,将其切割成短钢管出售,给定钢管长度和对应的价钱如下表:

问题要求根据上面的价格,给出最佳的切割方案,使得收益最大。
以n=4为例,可以将钢条切割成如下图所示的8种情况,其中收益最大的是(c):
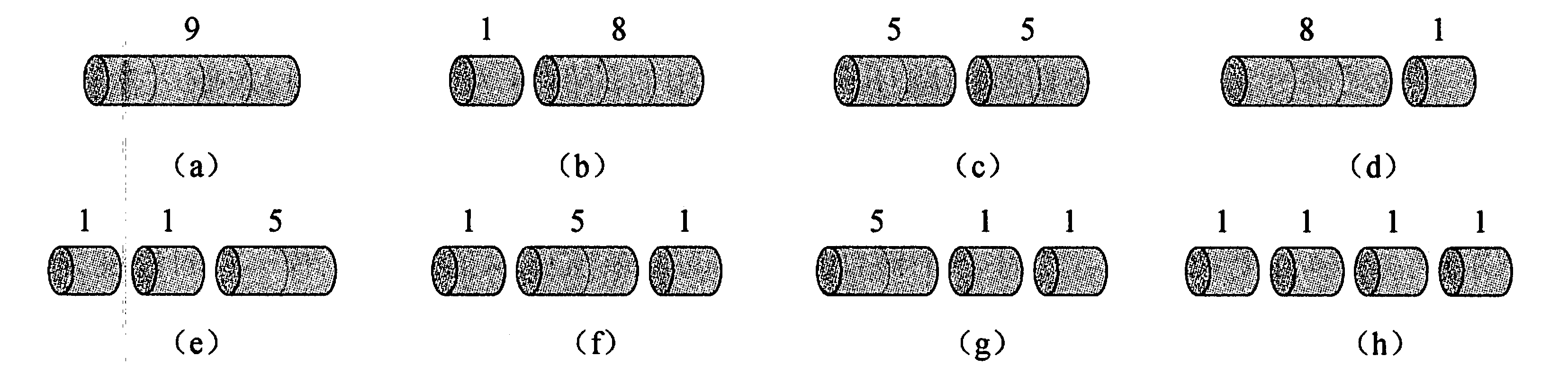
这个题的切入点非常重要,也就是——当知道长度为1到i的钢条的切割方案时,可以推导出长度为i+1的钢条如何切割最优。
我们定义长度=i,且长度为i时最优切割方案的收益是\(r_i\)
- i=1时, 当然不切割,即\(r_1=p_1\)
- i=2时,有两种方案,要么切一刀,要么不切,即\(r_2=max[p_2,r_1+r_1]\)
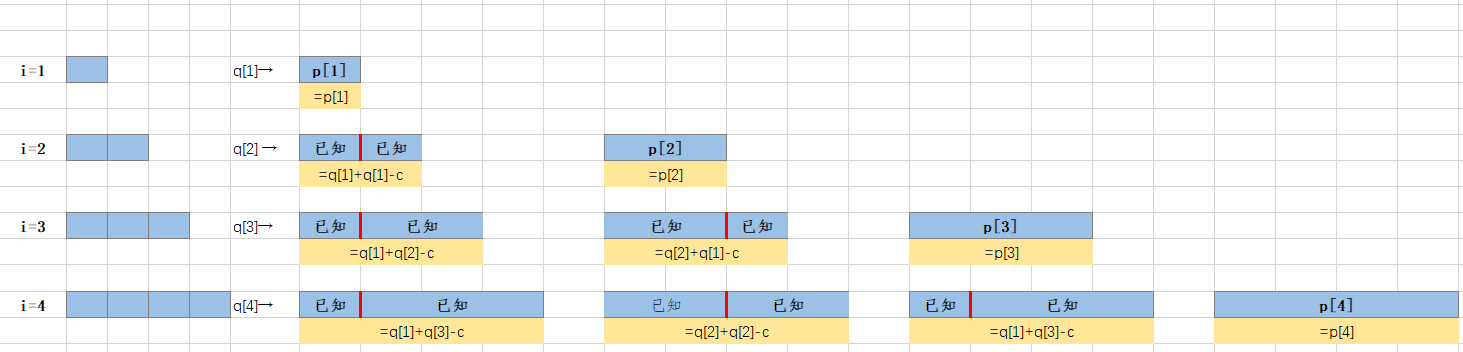
- i=3时,我们从下图可以看到,假设我们从它上面随便切一刀,我们会发现无论是左边还是右边都是已知的。即\(r_3=max[p_3,r_1+r_2,r_2+r_1]\)
- i=4时,还是可以看到,无论我们从哪里切一刀,会发现无论是左边还是右边,都是已知的!即\(r_4=max[p_4,r_1+r_3,r_2+r_2,r_3+r_1]\)

因此,我们可以用更短的钢条的最优切割收益来描述它:
\[r_n = max[p_n,r_1+r_{n-1},r_2+r_{n-2},...,r_{n-1}+r_1]\]
代码:
1 | public int[] q; |
钢条切割升级版
《算法导论》练习题15.1-3提出:除了切割下的钢条段具有不同价格\(p_i\)外,每次切割还要付出固定成本\(c\)。求修改后的钢条切割问题。
1 | public int[] q; |