堆(heap)又被为优先队列(priority queue)。尽管名为优先队列,但堆并不是队列。回忆一下,在队列 中,我们可以进行的限定操作是dequeue和enqueue。dequeue是按照进入队列的先后顺序来取出元素。而在堆中,我们不是按照元素进入队列的先后顺序取出元素的,而是按照元素的优先级取出元素。
这就好像候机的时候,无论谁先到达候机厅,总是头等舱的乘客先登机,然后是商务舱的乘客,最后是经济舱的乘客。每个乘客都有头等舱、商务舱、经济舱三种个键值(key)中的一个。头等舱->商务舱->经济舱依次享有从高到低的优先级。
Linux内核中的调度器(scheduler)会按照各个进程的优先级来安排CPU执行哪一个进程。计算机中通常有多个进程,每个进程有不同的优先级(该优先级的计算会综合多个因素,比如进程所需要耗费的时间,进程已经等待的时间,用户的优先级,用户设定的进程优先程度等等)。内核会找到优先级最高的进程,并执行。如果有优先级更高的进程被提交,那么调度器会转而安排该进程运行。优先级比较低的进程则会等待。“堆”是实现调度器的理想数据结构。
堆的性质
堆的实现通过构造二叉堆(binary heap),实为二叉树的一种;由于其应用的普遍性,当不加限定时,均指该数据结构的这种实现。这种数据结构具有以下性质:
以最大堆为例,最大堆指除了根节点以外的所有节点i都要满足\(A[PARENT(i)]\geq A[i]\)
堆是一颗完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
堆的应用场景
堆排序以及优先队列
堆的存储
由于我们需要频繁的对堆进行增加删除,所以一般堆的底层都是通过数组来实现(而不能用链表,因为链表需要频繁new 或 delete对象,非常慢)
因此堆的存储为,对于元素\(A[i]\) :
父节点:\(A[(i-1)/2]\) (右移1)
左孩子:\(A[2i + 1]\) (左移1,低位+1,可得到2i+1)
右孩子:\(A[2i+2]\) (左移1,低位+2,可得到2i+2)
堆的基本操作
堆的增删示意图如下所示:
维护某个节点的堆属性:MAX-HEAPIFY(A,i)
由于堆的建立是基于原来的数组的。假设我们现在已经有了一个半成品的堆。
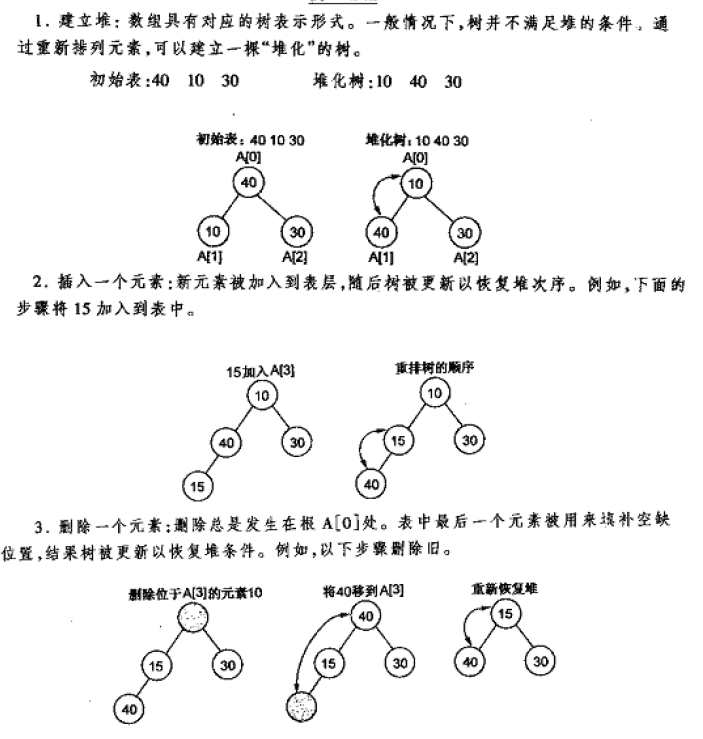
初始状态如下图所示。在节点i=2处,A[2]违背了最大堆性质,因为它≤它的孩子。
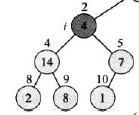
接下来我们找出i节点的孩子中最大的节点,即节点4,通过交换A[2]和A[4]的值,节点2恢复了最大堆的性质,如下图所示:
但此时又导致了节点4违反了最大堆的性质。此时只需要递归调用MAX-HEAPIFY(A,4),此时i=4,通过交换A[4]和A[9]的值,节点4的最大堆性质得到了恢复。如下图所示:
以上操作的伪代码为:
1 2 3 4 5 6 7 8 9 10 11 MAX-HEAPIFY(A,i) l = LEFT(i) r = RIGHT(i) if l<= A.heap-size and A[l]>A[i] largest = l else largest = i if r<= A.heap-size and A[r] > A[largest] largest = r if largest != i exchange A[i] with A[largest] MAX-HEAPIFY(A,largest)
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 private void swap (int p,int q) int temp = A[p]; A[p] = A[q]; A[q] = temp; } private void Heapify (int i) int l = 2 *i + 1 ; int r = 2 *i + 2 ; int largest = i; if (l<heapSise && A[l]>A[largest]){ largest = l; } if (r < heapSise && A[r] > A[largest]){ largest = r; } if (largest != i){ swap(i,largest); Heapify(largest); } }
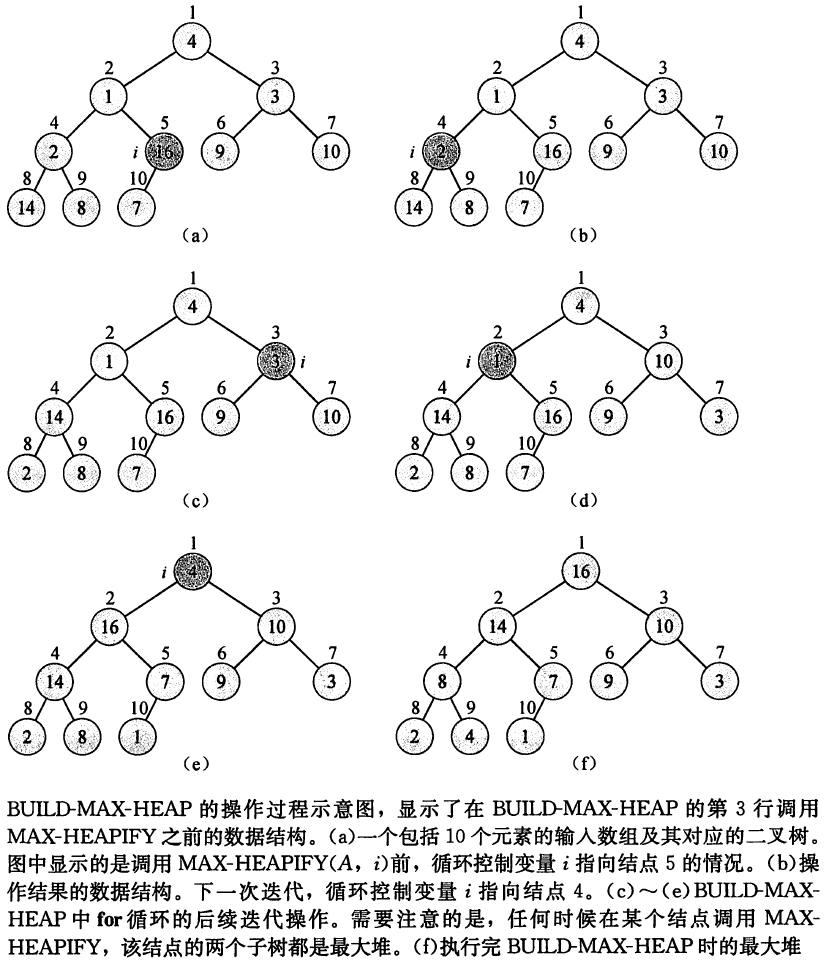
维护整个树的堆属性:BUILD-MAX-HEAP(A)
我们通过一个实例来说明具体的建堆步骤。
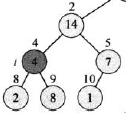
假设我们有数组4,1,3,2,16,9,10,14,8,7
它的形状为:
当然最暴力的方式就是从最后一个元素【7】开始,向上以此对树进行维护。但事实上由于后[n/2]个元素都是根节点,不需要进行维护。因此我们只需要维护前[n/2]个节点。
具体步骤如下图所示:
伪代码为:
1 2 3 4 BUILD-MAX-HEAP(A) A.heap.size = A.length for i = [A.length/2 ] downto 1 MAX-HEAPIFTY(A,i)
代码:
1 2 3 4 5 6 7 private void Build () for (int i = (heapSise-2 )/2 ; i>=0 ; i-=1 ){ Heapify(i); } }
复杂度
在高度为h的结点上运行MAX-HEAPIFY的代价是\(O(h)\) ,因此建树的总代价为:
\[\sum_{h=0}^{lgn}O(h)=O(n\sum_{h=0}^{lgn}\frac{h}{2^h})=O(n)\]
poll()
一般来说,删除元素对象针对于根节点。
删除掉根节点之后该怎么办呢?《算法导论》说直接把最后一个元素提上来就可以了。一开始想不通为什么,我想的是直接把左右孩子中的比较大的那个提上来,然后向下递归就可以了。但再仔细思索,如果这样操作,那这个孩子下面几乎所有的元素都要变化位置。然而如果直接把最后一个元素提上来,只需要变化一半。很神奇。
伪代码:
1 2 3 4 POP() swap(1 ,heapSize) heapSize -= 1 MAX-HEAPFITY(A,1 )
代码
1 2 3 4 5 6 7 8 public int pop () int e = A[0 ]; swap(0 ,heapSise-1 ); heapSise -= 1 ; Heapify(0 ); System.out.println(Arrays.toString(A)+'\t' +heapSise); return e; }
堆排序
堆排序其实只需要利用堆的性质——根节点最大,然后依次将根节点执行POP操作即可。
伪代码:
1 2 3 4 SORT() while heapSize > 0 : POP();
代码:
1 2 3 4 5 6 public void sort () while (heapSise>0 ){ pop(); } }
堆排序复杂度:
\(O(long(n!)) = O(nlogn)\)
堆排序总代吗:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 private int [] A;private int heapSise;public void sortIntegers (int [] A) heapSise = A.length; this .A = A; Build(); sort(); } private void swap (int p,int q) int temp = A[p]; A[p] = A[q]; A[q] = temp; } private void Heapify (int i) int l = 2 *i + 1 ; int r = 2 *i + 2 ; int largest = -1 ; if (l<heapSise && A[l]>A[i]){ largest = l; }else largest = i; if (r < heapSise && A[r] > A[largest]){ largest = r; } if (largest != i){ swap(i,largest); Heapify(largest); } } public int pop () int e = A[0 ]; swap(0 ,heapSise-1 ); heapSise -= 1 ; Heapify(0 ); return e; } public void sort () while (heapSise>0 ){ pop(); } } private void Build () for (int i = (heapSise-2 )/2 ; i>=0 ; i-=1 ){ Heapify(i); } }
HashHeap
Hash堆与普通堆的区别:Hash堆多了一个用来指示元素位置的索引。这个索引表示元素在堆中的位置。
add()
向堆中添加一个元素
将元素加到数组末尾
依次向上调整
1 2 3 4 5 6 7 8 9 10 11 12 13 void add (int now) size_t++; if (hash.containsKey(now)) { Node hashnow = hash.get(now); hash.put(now, new Node(hashnow.id, hashnow.num + 1 )); } else { heap.add(now); hash.put(now, new Node(heap.size() - 1 , 1 )); } siftup(heap.size() - 1 ); }
poll()
从堆顶拿走一个元素
将堆顶元素拿走
将堆尾元素放到堆顶
依次向下调整
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Integer poll () { size_t--; Integer now = heap.get(0 ); Node hashnow = hash.get(now); if (hashnow.num == 1 ) { swap(0 , heap.size() - 1 ); hash.remove(now); heap.remove(heap.size() - 1 ); if (heap.size() > 0 ) { siftdown(0 ); } } else { hash.put(now, new Node(0 , hashnow.num - 1 )); } return now; }
peak()
从堆顶拿出一个值,并不删除
delete()
删除指定元素now
根据hashMap找到now在数组中的位置
删除这个元素,并将末尾元素放到这个位置
向上、向下调整
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 void delete (int now) size_t--; ; Node hashnow = hash.get(now); int id = hashnow.id; int num = hashnow.num; if (hashnow.num == 1 ) { swap(id, heap.size() - 1 ); hash.remove(now); heap.remove(heap.size() - 1 ); if (heap.size() > id) { siftup(id); siftdown(id); } } else { hash.put(now, new Node(id, num - 1 )); } }
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 class HashHeap ArrayList<Integer> heap; String mode; int size_t; HashMap<Integer, Node> hash; class Node public Integer id; public Integer num; Node(Node now) { id = now.id; num = now.num; } Node(Integer first, Integer second) { this .id = first; this .num = second; } } public HashHeap (String mod) heap = new ArrayList<Integer>(); mode = mod; hash = new HashMap<Integer, Node>(); size_t = 0 ; } int peak () return heap.get(0 ); } int size () return size_t; } Boolean empty () { return (heap.size() == 0 ); } int parent (int id) if (id == 0 ) { return -1 ; } return (id - 1 ) / 2 ; } int lson (int id) return id * 2 + 1 ; } int rson (int id) return id * 2 + 2 ; } boolean comparesmall (int a, int b) if (a <= b) { if (mode == "min" ) return true ; else return false ; } else { if (mode == "min" ) return false ; else return true ; } } void swap (int idA, int idB) int valA = heap.get(idA); int valB = heap.get(idB); int numA = hash.get(valA).num; int numB = hash.get(valB).num; hash.put(valB, new Node(idA, numB)); hash.put(valA, new Node(idB, numA)); heap.set(idA, valB); heap.set(idB, valA); } Integer poll () { size_t--; Integer now = heap.get(0 ); Node hashnow = hash.get(now); if (hashnow.num == 1 ) { swap(0 , heap.size() - 1 ); hash.remove(now); heap.remove(heap.size() - 1 ); if (heap.size() > 0 ) { siftdown(0 ); } } else { hash.put(now, new Node(0 , hashnow.num - 1 )); } return now; } void add (int now) size_t++; if (hash.containsKey(now)) { Node hashnow = hash.get(now); hash.put(now, new Node(hashnow.id, hashnow.num + 1 )); } else { heap.add(now); hash.put(now, new Node(heap.size() - 1 , 1 )); } siftup(heap.size() - 1 ); } void delete (int now) size_t--; ; Node hashnow = hash.get(now); int id = hashnow.id; int num = hashnow.num; if (hashnow.num == 1 ) { swap(id, heap.size() - 1 ); hash.remove(now); heap.remove(heap.size() - 1 ); if (heap.size() > id) { siftup(id); siftdown(id); } } else { hash.put(now, new Node(id, num - 1 )); } } void siftup (int id) while (parent(id) > -1 ) { int parentId = parent(id); if (comparesmall(heap.get(parentId), heap.get(id)) == true ) { break ; } else { swap(id, parentId); } id = parentId; } } void siftdown (int id) while (lson(id) < heap.size()) { int leftId = lson(id); int rightId = rson(id); int son; if (rightId >= heap.size() || (comparesmall(heap.get(leftId), heap.get(rightId)) == true )) { son = leftId; } else { son = rightId; } if (comparesmall(heap.get(id), heap.get(son)) == true ) { break ; } else { swap(id, son); } id = son; } } }
Java的PriorityQueue
Integer最小堆实例
1 2 3 4 5 6 Queue<Integer> integerPriorityQueue = new PriorityQueue<>(7 ); Random rand = new Random(); integerPriorityQueue.add(new Integer(rand.nextInt(100 ))); Integer in = integerPriorityQueue.poll();
Integer最大堆实例
1 2 3 4 5 6 7 8 9 10 11 12 Queue<Integer> heap = new PriorityQueue<>(nums.length+1 ,idComparator); heap.add(e); heap.poll(); public static Comparator<Integer> idComparator = new Comparator<Integer>(){ @Override public int compare (Integer c1, Integer c2) return (int ) (c2 - c1); } };
自定义类的最小堆
1 2 3 4 5 6 7 8 9 10 11 12 13 Queue<Customer> cutomerPriorityQueue = new PriorityQueue<>(7 ,idComparator); customerPriorityQueue.add(new Customer(id, "Pankaj " +id)); Customer cust = customerPriorityQueue.poll(); public static Comparator<Customer> idComparator = new Comparator<Customer>(){ @Override public int compare (Customer c1, Customer c2) return (int ) (c1.getId() - c2.getId()); } };
相关leetcode题
TOP K问题也有多种解决方案,比如排序,最后截取靠前或者靠后的K个数据。当数据量小的时候,排序解决起来当然可以,算法简单,排序算法也有很多现成的。当数据量很大时,维护一个很长的数组,不管是空间存储上还是排序耗费的时间上都可能难以接受。这时我们可以采用最小堆的方式来实现,只需要维护一个K长度的数组就行。
然而具体到问题,就会有非常多的变种。
给一个数组[1,2,7,3,8,5,3,2] 。假如最开始只有三个[1,2,7] 。每次新加入一个元素。求每次加入后的所有数的中位数。如果是奇数个元素,就是中位数。如果是偶数个元素,返回较小的那个元素。
暴力方法
每次加入一个元素,就排序。然后求A[(n-1)/2]。 复杂度\(n^2logn\)
双堆方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 将数据分为: [比中位数小的] 中位数 [比中位数大的] 每次维护两边即可! [1 ,2 ,7 ] 来说,比2 小的有1 个,比2 大的有1 个。那么恰好2 就是中位数 [1 ,2 ,7 ,3 ] 来说,比2 小的有1 个,比2 大的有2 个,那么恰好2 就是中位数 [1 ,2 ,7 ,3 ,8 ] 来说,比2 小的有1 个,比2 大的有3 个,此时2 不是中位数了。因此就把2 放入左边堆,然后从右边堆里拿出来一个较小的,即3 ,那么就是新的中位数了! 以此类推 流程: -- O(nlogn) while (){ 1. add(val) --- O(logn) 2. 两边挪一挪,维护平衡 -- O(logn) }
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 class PirorityQueue private ArrayList<Integer> arr; private HashMap<Integer, Integer> arr_element_repeat; private HashMap<Integer, Integer> value2Idx; private int size; private int numsCounter; private String attribute; PirorityQueue(String attribute){ arr = new ArrayList<>(); size = 0 ; numsCounter = 0 ; arr_element_repeat = new HashMap<>(); value2Idx = new HashMap<>(); if (attribute.equals("max" ) || attribute.equals("min" )){ this .attribute = attribute; }else { System.out.println("初始化失败,参数错误" ); } } private int getNumsCounter () return numsCounter; } public void add (int value) ++numsCounter; if (arr_element_repeat.containsKey(value)){ arr_element_repeat.replace(value, arr_element_repeat.get(value) + 1 ); return ; } if (size < arr.size()){ arr.set(size, value); }else { arr.add(value); } value2Idx.put(value, size); ++size; shiftUp(size - 1 ); arr_element_repeat.put(value, 1 ); } public int peek () if (size == 0 ){ System.out.println("空堆,peek失败" ); return Integer.MIN_VALUE; }else return arr.get(0 ); } public int poll () if (size == 0 ) { System.out.println("空堆,poll失败" ); return Integer.MIN_VALUE; }else { int value = arr.get(0 ); --numsCounter; if (arr_element_repeat.getOrDefault(value, 0 ) > 1 ){ arr_element_repeat.replace(value, arr_element_repeat.get(value) - 1 ); }else { deleteByIndex(0 ); } return value; } } public void delete (int value) --numsCounter; if (arr_element_repeat.getOrDefault(value, 0 ) > 1 ){ arr_element_repeat.replace(value, arr_element_repeat.get(value) - 1 ); return ; } deleteByIndex(value2Idx.get(value)); } private void deleteByIndex (int index) arr_element_repeat.remove(arr.get(index)); --size; swap(index, size); shiftUp(index); shiftDown(index); } private void swap (int i, int j) int temp = arr.get(i); arr.set(i, arr.get(j)); arr.set(j, temp); value2Idx.put(arr.get(i), i); value2Idx.put(arr.get(j), j); } private void shiftDown (int index) if (index >= size) return ; int left = getLeft(index); int right = getRight(index); int largest = index; if (left < size && compare(arr.get(left), arr.get(largest)) > 0 ){ largest = left; } if (right < size && compare(arr.get(right), arr.get(largest)) > 0 ){ largest = right; } if (largest != index){ swap(largest, index); shiftDown(largest); } } private void shiftUp (int index) if (index < 0 ) return ; int father = getFather(index); if (father >= 0 && compare(arr.get(index), arr.get(father)) > 0 ){ swap(father, index); shiftUp(father); } } private int getLeft (int index) return (index << 1 ) + 1 ; } private int getRight (int index) return (index << 1 ) + 2 ; } private int getFather (int index) return (index-1 ) >> 1 ; } private int compare (int a, int b) if (attribute.equals("max" )){ return Integer.compare(a, b); }else { return Integer.compare(b,a); } } } PirorityQueue largerHeap; PirorityQueue smallerHeap; Integer meadian; public MedianFinder () largerHeap = new PirorityQueue("min" ); smallerHeap = new PirorityQueue("max" ); meadian = null ; } public void addNum (int num) if (smallerHeap.size > 0 ) { if (num >= smallerHeap.peek() && num <= largerHeap.peek()) { } else if (num >= smallerHeap.peek() && num < largerHeap.peek()) { largerHeap.add(num); num = largerHeap.poll(); } else if (num < smallerHeap.peek() && num <= largerHeap.peek()) { smallerHeap.add(num); num = smallerHeap.poll(); } else { largerHeap.add(num); num = largerHeap.poll(); } } if (meadian == null ) meadian = num; else { smallerHeap.add(Math.min(num, meadian)); largerHeap.add(Math.max(num, meadian)); meadian = null ; } } public double findMedian () if (meadian == null ){ return (smallerHeap.peek() + largerHeap.peek()) / 2.0 ; }else return meadian; }
给一个数组[1,2,7,3,8,5,3,2]。有一个大小为k=3的窗口。窗口每次向右移动一格,求每次窗口内的中位数
其实就是上题的follow up 。 只需要每次add之前将窗口左外的元素删除即可!
那么就涉及到了需要删除元素的堆!可以用hashHeap优化辣。
Kth Largest Element in an Array
给一个数组 [3,2,1,5,6,4] 和 k = 2, 输出第k大的值,5
这道题用一个最大堆完成即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 import java.util.Comparator;import java.util.PriorityQueue;import java.util.Queue;public class Main public int findKthLargest (int [] nums, int k) Queue<Integer> heap = new PriorityQueue<>(nums.length+1 ,idComparator); for ( int e : nums ){ heap.add(e); } while ( k>1 ){ heap.poll(); --k; } return heap.peek(); } public static Comparator<Integer> idComparator = new Comparator<Integer>(){ @Override public int compare (Integer c1, Integer c2) return (int ) (c2 - c1); } }; public static void main (String[] args) int [] nums = {3 ,2 ,1 ,5 ,6 ,4 }; int k = 2 ; System.out.println(new Main().findKthLargest(nums,k)); } }
还有一种更好写代码的方式。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class MedianFinder PriorityQueue<Integer> larger; PriorityQueue<Integer> smaller; public MedianFinder () larger = new PriorityQueue<Integer>(); smaller = new PriorityQueue<Integer>(new Comparator<Integer>() { @Override public int compare (Integer o1, Integer o2) return o2-o1; } }); } public void addNum (int num) if (larger.size() == smaller.size()){ if (smaller.size() == 0 ){ smaller.add(num); }else { var temp = larger.poll(); if (temp < num){ smaller.add(temp); larger.add(num); }else { smaller.add(num); larger.add(temp); } } }else { var temp = smaller.poll(); if (temp < num){ smaller.add(temp); larger.add(num); }else { smaller.add(num); larger.add(temp); } } } public double findMedian () if ((larger.size() + smaller.size()) % 2 == 0 ){ return ((double )larger.peek()+smaller.peek()) / 2 ; }else { return smaller.peek(); } } }
Top K Frequent Elements
给一个int[],输出频率最高的k个数字。
For example, Given [1,1,1,2,2,3] and k = 2, return [1,2].
思路:直接建一个堆,在遍历的同时对堆进行维护。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 class Solution class Node implements Comparable <Node > Integer s; int count; @Override public int compareTo (Node o) if (this .count > o.count){ return -1 ; }else if (this .count == o.count){ if (this .s.compareTo(o.s)>0 ){ return -1 ; }else { return 1 ; } }else { return 1 ; } } Node(Integer s,int count){ this .s = s; this .count = count; } } class HashHeap Node[] E; HashMap<Integer,Integer> map; int heapSize; int k; public HashHeap (int k) E = new Node[k+1 ]; heapSize = 0 ; map = new HashMap<>(); this .k = k ; } private int left (int i) if (i == 0 ) { return 2 ; } return 2 * i; } private int right (int i) return 2 * i + 1 ; } private int father (int i) if (i==1 ){ return 0 ; } return i/2 ; } private int brother (int i) if (i==0 ){ return 0 ; } if (i==1 ){ return 2 ; } if (i==2 ){ return 1 ; } if (i%2 ==0 ){ return i+1 ; }else { return i-1 ; } } private void swap (int p,int q) int indexq = map.get(E[q].s); map.replace(E[q].s,map.get(E[p].s)); map.replace(E[p].s,indexq); Node temp = E[p]; E[p] = E[q]; E[q] = temp; } public void Push (Node e) E[heapSize] = e; heapSize+=1 ; map.put(e.s,heapSize-1 ); FixUP(heapSize-1 ); } private void FixUP (int i) if (i==0 )return ; int father = father(i); if (E[father].compareTo(E[i])>0 ) { swap(i, father); } FixUP(father); } private Node Pop () if (heapSize==0 ){ return null ; } swap(0 ,heapSize-1 ); heapSize-=1 ; FixDown(0 ); return E[heapSize]; } private void FixDown (int i) int l = left(i); int r = right(i); int min = -1 ; if (l < this .heapSize && E[l].compareTo(E[i])<0 ){ min = l; }else { min = i; } if ( r < this .heapSize && E[r].compareTo(E[min])<0 ){ min = r; } if ( min != i ){ swap(i,min); FixDown(min); } } public void count_add1 (int s) int index = map.get(s); E[index].count+=1 ; FixUP(index); } } public List<Integer> topKFrequent (int [] nums, int k) HashHeap heap = new HashHeap(nums.length); for (int i = 0 ; i < nums.length ; i += 1 ){ if (heap.map.containsKey(nums[i])){ heap.count_add1(nums[i]); }else { heap.Push(new Node(nums[i],1 )); } } List<Integer> ans = new ArrayList<>(); for (int i = 0 ; i < k ; i += 1 ){ ans.add(heap.Pop().s); } return ans; } }
Kth Smallest Element in a Sorted Matrix,378
原题 给一个n*n的数组,行列都有序。找到第K小的元素。
1 2 3 4 5 6 7 8 9 matrix = [ [ 1, 5, 9], [10, 11, 13], [12, 13, 15] ], k = 8, return 13.
思路
如果这道题用堆来解决,思考过程如下:
k=1时,堆为[1],此时第一小为1
k=2时,第2小一定是1的右或下,那就将它两都放进去。而同时1不可能是第二小,那就提前把它拿出来。那么堆为[5,10],此时第2小为5
k=3时,第3小一定是5的右/下,或者就是10本身。而且不可能是5。此时堆为[9,10,11],那么第3小就是9
k=4时,第4小一定是9的右/下,或者就是10本身。而且不可能是9。此时堆为[10,11,12],那么第4小就是10
将以上思考过程写为代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Node implements Comparable <Node > int x; int y; int val; Node(int x,int y,int val){ this .x = x; this .y = y; this .val = val; } @Override public int compareTo (Node o1) return this .val - o1.val; } } public int kthSmallest (int [][] matrix, int k) if (matrix.length==0 || matrix[0 ].length==0 )return -1 ; boolean [][] hash = new boolean [matrix.length][matrix[0 ].length]; Queue<Node> priorityQueue = new PriorityQueue<>(k); Node top_i; for (int i=0 ;i<k;i+=1 ){ if (priorityQueue.size()==0 ){ priorityQueue.add(new Node(0 ,0 ,matrix[0 ][0 ])); }else { top_i = priorityQueue.poll(); if (top_i.x+1 <matrix[top_i.y].length && !hash[top_i.x+1 ][top_i.y]) { hash[top_i.x+1 ][top_i.y]=true ; priorityQueue.add(new Node(top_i.x + 1 , top_i.y, matrix[top_i.x + 1 ][top_i.y])); } if (top_i.y+1 <matrix.length && !hash[top_i.x][top_i.y+1 ]) { hash[top_i.x][top_i.y+1 ]=true ; priorityQueue.add(new Node(top_i.x, top_i.y + 1 , matrix[top_i.x][top_i.y + 1 ])); } } } return priorityQueue.peek().val; }
复杂度分析
由于堆的add和poll操作的复杂度都是log(m),其中m是堆的大小。
而此题堆长度不大于k,因此粗略来看总体复杂度为\(O(klog(k))\) 。
但经过我测试发现,假设输入数组为\(n \times n\) ,当\(k>n\) 时,堆长度是一定不大于n的。这里我有点想不通。
另一种堆的思路
以下这种方式,仅仅只需要向下遍历。我们从第一行构建初始的最小堆,每次从中移除一个元素,再从下一行的对应位置加一个元素进入最小堆(思考一下,这样做保证了所有元素按从小到大的顺序加入最小堆,同时不加入过多元素),执行k-1次这个过程,堆顶元素即为所求。
时间复杂度:O(klogn)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public class Solution public int kthSmallest (int [][] matrix, int k) int n = matrix.length; PriorityQueue<Tuple> pq = new PriorityQueue<Tuple>(); for (int j = 0 ; j <= n-1 ; j++) pq.offer(new Tuple(0 , j, matrix[0 ][j])); for (int i = 0 ; i < k-1 ; i++) { Tuple t = pq.poll(); if (t.x == n-1 ) continue ; pq.offer(new Tuple(t.x+1 , t.y, matrix[t.x+1 ][t.y])); } return pq.poll().val; } } class Tuple implements Comparable <Tuple > int x, y, val; public Tuple (int x, int y, int val) this .x = x; this .y = y; this .val = val; } @Override public int compareTo (Tuple that) return this .val - that.val; } }
骚操作——二分法
先找到数组的最大值和最小值,然后以此作为二叉搜索的左右两边,求出其中间值,然后看比该值小的有多少个,是否满足条件,如果满足条件就返回,不然就将左右边界修改为mid即可。代码入下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution public int kthSmallest (int [][] matrix, int k) int n = matrix.length; int lo = matrix[0 ][0 ], hi = matrix[n - 1 ][n - 1 ]; while (lo <= hi) { int mid = lo + (hi - lo) / 2 ; int count = getLessEqual(matrix, mid); if (count < k) lo = mid + 1 ; else hi = mid - 1 ; } return lo; } private int getLessEqual (int [][] matrix, int val) int res = 0 ; int n = matrix.length, i = n - 1 , j = 0 ; while (i >= 0 && j < n) { if (matrix[i][j] > val) i--; else { res += i + 1 ; j++; } } return res; } }
Find K Pairs with Smallest Sums
题目
You are given two integer arrays nums1 and nums2 sorted in ascending order and an integer k .
Define a pair (u,v) which consists of one element from the first array and one element from the second array.
Find the k pairs (u1,v1),(u2,v2) ...(uk,vk) with the smallest sums.
给定两个数组nums1和nums2,找到nums1[i] + nums2[i] 的从最小到第k小的对(i,j),并返回。
Example 1:
1 2 3 4 5 6 7 Given nums1 = [1,7,11], nums2 = [2,4,6], k = 3 Return: [1,2],[1,4],[1,6] The first 3 pairs are returned from the sequence: [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
Example 2:
1 2 3 4 5 6 7 Given nums1 = [1,1,2], nums2 = [1,2,3], k = 2 Return: [1,1],[1,1] The first 2 pairs are returned from the sequence: [1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]
Example 3:
1 2 3 4 5 6 Given nums1 = [1,2], nums2 = [3], k = 3 Return: [1,3],[2,3] All possible pairs are returned from the sequence: [1,3],[2,3]
这道题与上一道题非常像。要注意的有几点:
并没有说两个数组已排序;
并没有说k会小于num1.length * nums2.length
思路
首先将nums1和nums2排序,然后列出如下表:
2
2+1
2+7
2+4
4
4+1
4+7
4+4
6
6+1
6+7
6+4
然后这道题就转化成了上一道题!按照上一道题的思路解即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class Solution class Node implements Comparable <Node > int x; int y; int val; Node(int x,int y,int val){ this .x = x; this .y = y; this .val = val; } @Override public int compareTo (Node o1) return this .val - o1.val; } } public List<int []> kSmallestPairs(int [] nums1, int [] nums2, int k) { List<int []> result = new ArrayList<>(); if (nums1.length==0 || nums2.length==0 || k==0 ) return result; if (k>nums1.length*nums2.length) k = nums1.length*nums2.length; Arrays.sort(nums1); Arrays.sort(nums2); int i,x,y; Queue<Node> priorityQueue = new PriorityQueue<>(k); for (i=0 ;i<nums1.length;i+=1 ){ priorityQueue.offer(new Node(i,0 ,nums2[0 ]+nums1[i])); } Node temp; k-=1 ; for (i = 0 ; i < k ; i+=1 ){ temp = priorityQueue.poll(); x = temp.x; y = temp.y; int [] aRes = {nums1[x],nums2[y]}; result.add(aRes); if (y+1 <nums2.length) priorityQueue.offer(new Node(x,y+1 ,nums1[x]+nums2[y+1 ])); } temp = priorityQueue.poll(); x = temp.x; y = temp.y; int [] aRes = {nums1[x],nums2[y]}; result.add(aRes); return result; } }
Merge k Sorted Lists
这道题给了k个链表ListNode[k] lists。每个链表都已排序。将这k个链表merge为一个有序链表。
思路:由于每次都要拿出最小的,那么一种解法就是用维护一个最小堆,最小堆的元素由当前的表头元素组成。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 import java.util.Comparator;import java.util.PriorityQueue;import java.util.Queue;public class Main public class ListNode int val; ListNode next; ListNode(int x){ val = x; } } class Node implements Comparable <Node > int val; int idx; Node(int val,int idx){ this .val = val ; this .idx = idx ; } @Override public int compareTo (Node o) return this .val - o.val; } } Queue<Node> priorityQueue; public ListNode add (ListNode list,int idx) priorityQueue.add(new Node(list.val,idx)); list = list.next; return list; } public ListNode mergeKLists (ListNode[] lists) if ( lists.length == 0 )return null ; priorityQueue = new PriorityQueue<>(lists.length); int hashCount = 0 ; boolean [] hash = new boolean [lists.length]; for ( int i = 0 ; i < lists.length ; ++i ){ if ( null == lists[i] ){ hash[i] = true ; ++hashCount; }else { lists[i] = add(lists[i],i); } } if ( hashCount == lists.length ){ return null ; } Node min = priorityQueue.poll(); ListNode root = new ListNode(min.val); if (null != lists[min.idx]) { lists[min.idx] = add(lists[min.idx], min.idx); }else { if ( !hash[min.idx] ){ hash[min.idx] = true ; ++hashCount; } } if ( hashCount == lists.length ){ return root; } ListNode r = root; while (true ) { min = priorityQueue.poll(); ListNode temp = new ListNode(min.val); r.next = temp; r = r.next; if (null != lists[min.idx]) { lists[min.idx] = add(lists[min.idx], min.idx); }else { if ( ! hash[min.idx] ){ hash[min.idx] = true ; ++hashCount; } } if (hashCount == lists.length){ break ; } } return root; } public ListNode insert (int [] a) ListNode root = new ListNode(a[0 ]); ListNode r = root; for ( int i = 1 ; i < a.length ; ++i ){ ListNode l = new ListNode(a[i]); r.next = l; r = r.next; } return root; } public static void main (String[] args) int [] a1 = {1 }; int [] a2 = {2 ,4 ,6 ,8 }; Main t = new Main(); ListNode[] lists = new ListNode[1 ]; lists[0 ] = t.insert(a1); t.mergeKLists(lists); } }
但是!还有一种更骚的操作! !把每个LinkNode看做一个元素:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 private Comparator<ListNode> ListNodeComparator = new Comparator<ListNode>() { public int compare (ListNode left, ListNode right) return left.val - right.val; } }; public ListNode mergeKLists (List<ListNode> lists) if (lists == null || lists.size() == 0 ) { return null ; } Queue<ListNode> heap = new PriorityQueue<ListNode>(lists.size(), ListNodeComparator); for (int i = 0 ; i < lists.size(); i++) { if (lists.get(i) != null ) { heap.add(lists.get(i)); } } ListNode dummy = new ListNode(0 ); ListNode tail = dummy; while (!heap.isEmpty()) { ListNode head = heap.poll(); tail.next = head; tail = head; if (head.next != null ) { heap.add(head.next); } } return dummy.next; }
这道题非常繁琐。要设计一个twitter类,使得它能够实现以下功能:
postTweet(userId, tweetId) : 发tweetgetNewsFeed(userId) : 返回用户userId关注好友的最近10个feed流,并按发表时间输出follow(followerId, followeeId) : Follower 关注 followee.unfollow(followerId, followeeId) : Follower取关 followee(如果它想取关它自己,就什么都不做)
思路:这道题主要要设计很多类。核心算法与上一题相同,一定要参考上一题的解法二。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 import java.lang.reflect.Array;import java.util.*;public class Twitter HashMap<Integer,User> users; private int time; public Twitter () users = new HashMap<>(); time = 0 ; } public int timego () ++this .time; return this .time; } class tweet implements Comparable <tweet > int tweetId; int userId; int time; tweet(int tweetId,int userId, int time){ this .tweetId = tweetId; this .time = time; this .userId = userId; } @Override public int compareTo (tweet o) return o.time - this .time; } } class ListTweet implements Comparable <ListTweet > tweet tw; ListTweet next; ListTweet(){ tw = null ; next = null ; } ListTweet(tweet tw){ this .tw = tw; } @Override public int compareTo (ListTweet o) return this .tw.compareTo(o.tw); } } class User int userId; ListTweet feed; ListTweet feed_readed; HashSet<Integer> follows; int helper; User(int userId){ this .userId = userId; feed = new ListTweet(); follows = new HashSet<>(); follows.add(userId); helper = 0 ; } public void post (int tweetId) ListTweet tw = new ListTweet(new tweet(tweetId,this .userId,timego())); tw.next = this .feed; this .feed = tw; } public void setFollows (int followId) if (!follows.contains(followId)) follows.add(followId); } public void unFollow (int folleeId) if (follows.contains(folleeId)){ follows.remove(folleeId); } } } public void postTweet (int userId, int tweetId) if ( ! users.containsKey(userId) ){ users.put(userId,new User(userId)); } users.get(userId).post(tweetId); } public List<Integer> getNewsFeed (int userId) List<Integer> result = new ArrayList<>(); Queue<ListTweet> feeds = new PriorityQueue<>(10 ); if ( !users.containsKey(userId) ){ return result; } User user = users.get(userId); HashSet<Integer> follows = user.follows; for ( Integer f : follows ){ ListTweet f_feeds = users.get(f).feed; if (null != f_feeds.tw)feeds.offer(f_feeds); } int i = 0 ; while (!feeds.isEmpty()){ ListTweet head = feeds.poll(); result.add(head.tw.tweetId); if (null != head.next.tw)feeds.offer(head.next); ++i; if ( i == 10 ){ break ; } } return result; } public void follow (int followerId, int followeeId) if (! users.containsKey(followeeId) ){ users.put(followeeId,new User(followeeId)); } if (! users.containsKey(followerId) ){ users.put(followerId,new User(followerId)); } User er = users.get(followerId); er.setFollows(followeeId); } public void unfollow (int followerId, int followeeId) if (followeeId == followerId)return ; if (! users.containsKey(followeeId) ){ users.put(followeeId,new User(followeeId)); return ; } if (! users.containsKey(followerId) ){ users.put(followerId,new User(followerId)); return ; } User er = users.get(followerId); er.unFollow(followeeId); } public static void main (String[] args) Twitter twitter = new Twitter(); twitter.postTweet(1 , 1 ); System.out.println(twitter.getNewsFeed(1 )); twitter.follow(2 , 1 ); System.out.println(twitter.getNewsFeed(2 )); twitter.postTweet(2 , 6 ); System.out.println(twitter.getNewsFeed(1 )); twitter.unfollow(1 , 2 ); System.out.println(twitter.getNewsFeed(1 )); } }
Split Array into Consecutive Subsequences
给一个数组[1,2,3,3,4,5],问它能不能分成多个长度大于3的连续子数组[1,2,3]和[3,4,5]。
思路:对我来说较难。很绕。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ==================step 1 ================== a = [1 ,2 ,3 ] ==================step 2 ================== a = [1 ,2 ,3 ] b = [3 ] ==================step 3 ================== a = [1 ,2 ,3 ] b = [3 ,4 ] ==================step 4 ================== a = [1 ,2 ,3 ] b = [3 ,4 ,5 ] ==================step 5 ==================
其实这个过程我们只需要维护每个子数组的最大值!
维护一个hashMap,key是当前某子数组的最大值,value是子数组的长度。由于同一个key可能对应多个value,且每次我们都要取最小值。因此我们将value设置为一个最小堆。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public boolean isPossible (int [] nums) HashMap<Integer,Queue<Integer>> helper = new HashMap<>(); Queue<Integer> heap; int min_count; for ( int n : nums ){ if ( helper.containsKey(n-1 ) ){ heap = helper.get(n-1 ); min_count = heap.poll()+1 ; if ( heap.isEmpty() ) helper.remove(n-1 ); }else { min_count = 1 ; } if ( !helper.containsKey(n) ){ helper.put(n,new PriorityQueue<>()); } heap = helper.get(n); heap.offer(min_count); } for (Map.Entry<Integer, Queue<Integer>> key : helper.entrySet()){ heap = key.getValue(); while (!heap.isEmpty()){ if (heap.poll() < 3 ){ return false ; } } } return true ; }
Trapping Rain Water II
给一个二维数组,假设这是一个台子。边界没有挡板。求问这个台子最多能乘多少雨水。
1 2 3 4 5 6 [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ] 返回4
这道题相对来说比较难。思路就是用堆维护一个最小边界,每次根据这个最小边界进行填水。
维护一个最小堆,保存最外面一圈的高度,因为最矮的格子决定了水能存放多少
每次取最小高度 h,与周围4个中没有被访问过的元素进行比较
如果该元素的高度小于 h,则注水到其中,并将其加入到最小堆中,设置该元素被访问过
如果该元素的高度大于 h,则直接将其加入到最小堆中,设置改元素被访问过
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 class Solution class Node implements Comparable <Node > int h; int i; int j; Node(int h,int i,int j){ this .h = h; this .i = i; this .j = j; } @Override public int compareTo (Node o) return this .h - o.h; } } public int trapRainWater (int [][] heightMap) if ( heightMap.length <= 2 || heightMap[0 ].length <= 2 )return 0 ; Queue<Node> heap = new PriorityQueue<>(); int [] bound_j = {0 ,heightMap[0 ].length-1 }; int [] bound_i = {0 ,heightMap.length-1 }; boolean [][] hash = new boolean [heightMap.length][heightMap[0 ].length]; int i,j; int count = heightMap.length * heightMap[0 ].length ; for ( int b : bound_i ){ for ( j = 0 ; j < heightMap[0 ].length ; ++j ){ heap.offer(new Node(heightMap[b][j],b,j)); hash[b][j] = true ; --count; } } for ( int b : bound_j ){ for ( i = 1 ; i < heightMap.length-1 ; ++i ){ heap.offer(new Node(heightMap[i][b],i,b)); hash[i][b] = true ; --count; } } Node min; int [] ii = {0 ,0 ,1 ,-1 }; int [] jj = {1 ,-1 ,0 ,0 }; int result = 0 ; int k; while (count > 0 ){ min = heap.poll(); for ( k = 0 ; k < ii.length ; ++k ){ i = min.i + ii[k]; j = min.j + jj[k]; if ( i < 0 || i >= hash.length || j < 0 || j >= hash[0 ].length )continue ; if (!hash[i][j]){ if (min.h > heightMap[i][j]){ result += min.h - heightMap[i][j]; heightMap[i][j] = min.h; } heap.offer(new Node(heightMap[i][j],i,j)); hash[i][j] = true ; --count; } } } return result; } }
The Skyline Problem
题意:给一些大楼int[][] build,每个楼是三元组[left,right,h]。如[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ]。求这些大楼的关键点。即求这些点:
输出为:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]
这题好难啊!!!
出发点:
左顶点出现伴随着这栋楼开始
右顶点出现伴随着这栋楼结束
一旦哪个顶点处的max_height与前一个不一样,那这个就是key point了!
思路 :借助大顶堆维护当前最高的楼,时间O(NlogN) 空间O(N)。 1 把这些矩形拆成两个点,一个左上顶点,一个右上顶点。将所有顶点按照横坐标排序后,开始遍历这些点。 2 遍历时,通过一个大顶堆来得知当前图形的最高位置。堆顶是所有顶点中最高的点,只要这个点没被移出堆,说明这个最高的矩形还没结束。 3 对于左顶点,我们将其加入堆中。对于右顶点,我们找出堆中其相应的左顶点,然后移出这个左顶点,同时也意味这这个矩形的结束。 4 代码中,为了区分左右顶点,左顶点高度值是负数,而右顶点高度值则存的是正数。注意,堆中先加入一个0高度,帮助我们在只有最矮的建筑物时选择最低值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 import java.util.*;public class Main public List<int []> getSkyline(int [][] buildings) { List<int []> result = new ArrayList<>(); List<int []> height = new ArrayList<>(); for ( int [] b : buildings ){ height.add(new int []{b[0 ],-b[2 ]}); height.add(new int []{b[1 ],b[2 ]}); } Collections.sort(height,(a,b) -> { if ( a[0 ] != b[0 ] ) return a[0 ] - b[0 ]; else return a[1 ] - b[1 ]; }); Queue<Integer> pq = new PriorityQueue<>(11 , (i1,i2) -> (i2-i1)); pq.offer(0 ); int prev = 0 ; for ( int [] h : height ){ if ( h[1 ] < 0 ){ pq.offer(-h[1 ]); }else { pq.remove(h[1 ]); } int cur = pq.peek(); if ( prev != cur ){ result.add(new int []{h[0 ],cur}); prev = cur; } } return result; } public static void main (String[] args) int [][] nums = { {2 ,9 ,10 }, {3 ,7 ,15 }, {5 ,12 ,12 }, {15 ,20 ,10 }, {19 ,24 ,8 } }; Main t = new Main(); System.out.println(t.getSkyline(nums)); } }
参考文献
纸上谈兵:堆 数据结构系列-堆 The Skyline Problem - 天际线问题