子序列:
有序列\(X=<x_1,x_2,...,x_m>\),另一个子序列\(Z=<z_1,z_2,...,z_k>\),且Z是按顺序从X中挑出来的。可以跳着挑。
最长公共子序列(LCS)
从两个序列X和Y中,找到最长的公共子序列。
思路
这道题有一个非常巧妙的办法。我们先定义\(c[i,j]表示X_i和Y_j\)的最长公共子序列的长度,那么:
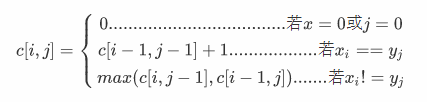
公式没显示出来。截成图了。 \[
c[i,j] = \left\{
\begin{array}{c}
0 \text{....................................}若x=0 或 j=0\\
c[i-1,j-1]+1 \text{..................}若x_i==y_j \\
max(c[i,j-1],c[i-1,j])\text{.......} 若x_i!=y_j
\end{array}
\right.
\]
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public int LCS(String[] s1,String [] s2){
int i,j;
int n = s1.length, m = s2.length;
int[][] c = new int[n][m];
if(s1[0] == s2[0]){c[0][0] = 1;}
for( i = 1 ; i < n ; i+=1 ){
if(s1[i] == s2[0]){c[i][0] = c[i-1][0] + 1; }
else{c[i][0] = c[i-1][0];}
}
for( j = 1 ; j < m ; j+=1 ){
if(s1[0] == s2[j]){c[0][j] = c[0][j-1] + 1; }
else{c[0][j] = c[0][j-1];}
}
for( i = 1 ; i < n ; i+=1 ){
for( j = 1 ; j < m ; j+=1 ){
if( s1[i]==s2[j] ){
c[i][j] = c[i-1][j-1] + 1;
}else{
c[i][j] = Math.max( c[i-1][j] , c[i][j-1] );
}
}
}
return c[n-1][m-1];
}
|