Trie树，即字典树/前缀树，又称单词查找树或键树，是一种树形结构。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是最大限度地减少无谓的字符串比较，查询效率比较高。

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

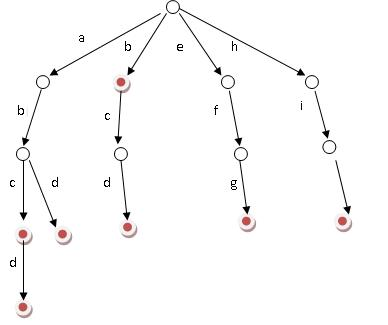
例如有abc,abcd,abd,b,bcd,efg,hii这7个单词，我们构建的树如下所示：

如上图所示，对于每一个节点，从根遍历到他的过程就是一个单词，如果这个节点被标记为红色，就表示这个单词存在，否则不存在。

那么，对于一个单词，我只要顺着他从根走到对应的节点，再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色，就相当于插入了这个单词。

这样一来我们查询和插入可以一起完成（重点体会这个查询和插入是如何一起完成的，稍后，下文具体解释），所用时间仅仅为单词长度，在这一个样例，便是10。我们可以看到，trie树每一层的节点数是26^i级别的。所以为了节省空间。我们用动态链表，或者用数组来模拟动态。空间的花费，不会超过单词数×单词长度。

它有3个基本性质：

根节点不包含字符，除根节点外每一个节点都只包含一个字符。
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。

实现

HashMap方式

这是总容易想到的方式。每个TrieNode节点的形状如表所示：

boolean	HashMap<char,TrieNode>
hasWord	children

代码：

HashMap<Character,Trie> children ;
boolean hasWord;
/*初始化*/
public Trie(){
  children = new HashMap<>();
  hasWord = false;
}
/*插入一个词*/
public void insert(String word){
  int length = word.length();
  Trie root = this;
  char c;
  for(int i = 0 ; i < length ; i += 1){
    c = word.charAt(i);
    if(!root.children.containsKey(c)){
      root.children.put(c,new Trie());
    }
    root = root.children.get(c);
  }
  root.hasWord = true;
}
/*查找*/
public boolean search(String word){
  int length = word.length();
  Trie root = this;
  char c;
  for(int i = 0 ; i < length ; i += 1){
    c = word.charAt(i);
    if(root.children.containsKey(c)){
      root = root.children.get(c);
    }else{
      return false;
    }
  }
  if(root.hasWord)return true;
  else return false;
}
/*返回prefix是否是树中某个单词的前缀*/
public boolean startsWith(String prefix){
  int length = prefix.length();
  Trie root = this;
  char c;
  for(int i = 0 ; i < length ; i += 1){
    c = prefix.charAt(i);
    if(root.children.containsKey(c)){
      root = root.children.get(c);
    }else{
      return false;
    }
  }
  return true;
}

数组方式

由于字母一共就26个。所以可以映射的方式将字母映射到长度为26的数组上，而下标就是字母。

class TrieNode {
        TrieNode[] next;
        boolean isWord;
        public TrieNode() {
            this.next = new TrieNode[26];
            this.isWord = false;
        }
    }
    
    TrieNode root;
    
    /** Initialize your data structure here. */
    public Trie() {
        this.root = new TrieNode();
    }
    
    /** Inserts a word into the trie. */
    public void insert(String word) {
        TrieNode cur = this.root;
        char[] w = word.toCharArray(); // 这是个骚操作，将str转化为char[]
        for(int i=0; i< word.length(); i++) {
            if(cur.next[w[i]-'a']==null) {
                cur.next[w[i]-'a'] = new TrieNode();
            }
            cur = cur.next[w[i]-'a'];
        }
        cur.isWord = true;
    }
    
    /** Returns if the word is in the trie. */
    public boolean search(String word) {
        // return startsWith(word) && 
        char[] w = word.toCharArray();
        TrieNode cur = root;
        for(int i=0; i< word.length(); i++) {
            if(cur.next[w[i]-'a']==null) return false;
            cur = cur.next[w[i]-'a'];
        }
        
        return cur.isWord;
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    public boolean startsWith(String prefix) {
        if(prefix.length()==0) return true;
        
        char[] word = prefix.toCharArray();
        TrieNode cur = root;
        for(int i=0; i< prefix.length(); i++) {
            if(cur.next[word[i]-'a']==null) return false;
            cur = cur.next[word[i]-'a'];
        }
        
        return true;
    }

问题实例

1、一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析

提示：用trie树统计每个词出现的次数，时间复杂度是O(nle)（le表示单词的平均长度），然后是找出出现最频繁的前10个词。当然，也可以用堆来实现，时间复杂度是O(nlg10)。所以总的时间复杂度，是O(nle)与O(nlg10)中较大的哪一个。

2、寻找热门查询

原题：搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复读比较高，虽然总数是1千万，但是如果去除重复和，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。

提示：利用trie树，关键字域存该查询串出现的次数，没有出现为0。最后用10个元素的最小推来对出现频率进行排序。

相关leetcode题

Implement Trie (Prefix Tree)

实现Trie树即可。如上代码所示。不做过多介绍。

Add and Search Word - Data structure design

实现如下接口：

void addWord(word)
bool search(word)
例如：
addWord("bad")
addWord("dad")
addWord("mad")
search("pad") -> false
search("bad") -> true
search(".ad") -> true
search("b..") -> true

即，添加字符串。当查找时，'.'可作为通配符。

思路：用Trie树即可。需要注意通配符的使用，需要进行依次遍历。

/**
 * Created by jiayi on 2017/11/13.
 */
public class WordDictionary {
    WordDictionary[] children;
    boolean hasWord;
    /*初始化*/
    public WordDictionary(){
        children = new WordDictionary[27];
        hasWord = false;
    }
    /*插入一个词*/
    public void addWord(String word){
        int length = word.length();
        WordDictionary root = this;
        int pos;
        for(int i = 0 ; i < length ; i += 1){
            pos = word.charAt(i) - 'a';
            if(null == root.children[pos]){
                root.children[pos] = new WordDictionary();
            }
            root = root.children[pos];
        }
        root.hasWord = true;
    }
    /*查找*/
    public boolean dfs(String word, int index,WordDictionary root){
        int length = word.length();
        int pos;
        for(int i = index ; i < length ; i += 1){
            pos = word.charAt(i) - 'a';
            if( pos == -51 ){
                for(int j = 0 ; j < 26 ; j += 1){
                    if(null != root.children && dfs(word,i+1,root.children[j])){
                        return true;
                    }
                }
                return false;
            }
            else if(null != root.children[pos]){
                root = root.children[pos];
            }else{
                return false;
            }
        }
        return root.hasWord;
    }
    public boolean search(String word){
        return dfs(word,0,this);
    }

    public static void main(String[] args){
        WordDictionary obj = new WordDictionary();
        obj.addWord("at");
        obj.addWord("and");
        obj.addWord("add");
        obj.addWord("a");
        obj.addWord("bat");
        System.out.println(obj.search("a.d."));

    }
}

Top K Frequent Words

给一组str[]，统计频率最高的k个str，并输出

如果两个str频率一样，则字典顺序低的str优先输出

Example 1:

1
2
3

Input: ["i", "love", "leetcode", "i", "love", "coding"], k = 2
Output: ["i", "love"]
i和love是频率最高的两个str，且频率都是2。i在love前面，因为i的字典顺序靠前

Example 2:

1 2	Input: ["the", "day", "is", "sunny", "the", "the", "the", "sunny", "is", "is"], k = 4 Output: ["the", "is", "sunny", "day"]

思路：这道题先用trie树进行统计，然后用一个最大堆来维护当前每个str的次数。当统计结束时，从堆顶输出k次即可。

class Solution {
    class Node implements Comparable<Node>{
            String s;
            int count;
            @Override
            public int compareTo(Node o) {
                if(this.count > o.count){
                    return -1;
                }else if(this.count == o.count){
                    if(this.s.compareTo(o.s)>0){
                        return 1;
                    }else{
                        return -1;
                    }
                }else{
                    return 1;
                }
            }
            Node(String s,int count){
                this.s = s;
                this.count = count;
            }
        }
    class HashHeap{
        Node[] E;
        HashMap<String,Integer> map;
        int heapSize;
        int k;
        public HashHeap(int k) {
            E = new Node[k+1];
            heapSize = 0;
            map = new HashMap<>();
            this.k = k ;
        }
        private int left(int i) {
            if (i == 0) {
                return 2;
            }
            return 2 * i;
        }
        private int right(int i) {
            return 2 * i + 1;
        }
        private int father(int i){
            if(i==1){
                return 0;
            }
            return i/2;
        }
        private int brother(int i){
            if(i==0){
                return 0;
            }
            if(i==1){
                return 2;
            }
            if(i==2){
                return 1;
            }
            if(i%2==0){
                return i+1;
            }else{
                return i-1;
            }
        }
        private void swap(int p,int q){
            int indexq = map.get(E[q].s);
            map.replace(E[q].s,map.get(E[p].s));
            map.replace(E[p].s,indexq);
            Node temp = E[p];
            E[p] = E[q];
            E[q] = temp;
        }
        public void Push(Node e){
    //        while(heapSize >= k){
    //            this.Pop();
    //        }
            E[heapSize] = e;
            heapSize+=1;
            map.put(e.s,heapSize-1);
            FixUP(heapSize-1);
    
        }
        private void FixUP(int i){
            if(i==0)return;
            int father = father(i);
            if(E[father].compareTo(E[i])>0) {
                swap(i, father);
            }
            FixUP(father);
        }
        private Node Pop(){
            if(heapSize==0){
                return null;
            }
            swap(0,heapSize-1);
            heapSize-=1;
            FixDown(0);
            return E[heapSize];
    
        }
        private void FixDown(int i) {
            int l = left(i);
            int r = right(i);
            int min = -1;
            if (l < this.heapSize && E[l].compareTo(E[i])<0){
                min = l;
            }else{
                min = i;
            }
            if( r < this.heapSize && E[r].compareTo(E[min])<0 ){
                min = r;
            }
            if( min != i ){
                swap(i,min);
                FixDown(min);
            }
        }
        public void count_add1(String s){
            int index = map.get(s);
            E[index].count+=1;
            FixUP(index);
        }
    
    }
    class Trie {
        Trie[] children;
        int wordCount;
        /*初始化*/
        public Trie(){
            children = new Trie[26];
            wordCount = 0;
    
        }
        /*插入一个词*/
        public void addWord(String word){
            int length = word.length();
            Trie root = this;
            int pos;
            for(int i = 0 ; i < length ; i += 1){
                pos = word.charAt(i) - 'a';
                if(null == root.children[pos]){
                    root.children[pos] = new Trie();
                }
                root = root.children[pos];
            }
            root.wordCount += 1;
          // 这里维护一个hashheap
            if(root.wordCount==1){
                heap.Push(new Node(word,1));
            }else{
                heap.count_add1(word);
            }
         
        }
    }
    HashHeap heap ;
    public List<String> topKFrequent(String[] words, int k) {
        List<String> ans = new ArrayList<>();
        Trie trie = new Trie();
        heap = new HashHeap(words.length);
        for(String w : words){
            trie.addWord(w);
        }
        for(int i = 0 ; i < k ; i +=1 ){
            ans.add(heap.Pop().s);
        }

        return ans;
    }
}

Map Sum Pairs

实现如下接口：

insert(String s,int val) --- s是关键字，val是价值

sum(String prefix) --- 输出以prefix为前缀的所有单词的价值和。

Input: insert("apple", 3), Output: Null
Input: sum("ap"), Output: 3
Input: insert("app", 2), Output: Null
Input: sum("ap"), Output: 5

思路：用Trie树保存insert之后的str，并给每一个节点保存一个val值。如果这个节点不是单词，val就为0。

/**
 * Created by jiayi on 2017/11/14.
 */
public class MapSum {
    class Node{
        Node[] children;
        int Val;
        Node(){
            children = new Node[26];
            Val = 0;
        }
        public void SetVal(int Val){
            this.Val = Val;
        }
    }
    /*初始化*/
    Node root;
    public MapSum() {
        root = new Node();
    }
    /*插入*/
    public void insert(String key, int val) {
        int index;
        Node e = root;
        for(int i = 0 ; i < key.length() ; i += 1){
            index = key.charAt(i) - 'a';
            if(null == e.children[index]){
                e.children[index] = new Node();
            }
            e = e.children[index];
        }
        e.SetVal(val);
    }
    /*前缀尾prefix的单词的权重和*/
    public int sum(String prefix) {
        int index;
        Node e = this.root;
        for( int i = 0 ; i < prefix.length() ; i += 1 ){
            index = prefix.charAt(i) - 'a';
            if( null != e.children[index] ){
                e = e.children[index];
            }else {
                return 0;
            }
        }
        // e停留在前缀末尾
        return dfs(e);
    }
    private int dfs(Node root){
        int val = root.Val;
        for( int i = 0 ; i < 26; i += 1 ){
            if( null == root.children[i] ){
                continue;
            }
            val += dfs(root.children[i]);
        }
        return val;

    }
    public static void main(String[] args){
        MapSum t = new MapSum();
        t.insert("a",3);
        System.out.println(t.sum("ap"));
        t.insert("b",2);
        System.out.println(t.sum("a"));
    }
}

Word Search II

给一个char[][] board，和一个String[] words。从words中找到被包含在board中的单词。

words = ["oath","pea","eat","rain"] and board =

[
  ['o','a','a','n'],
  ['e','t','a','e'],
  ['i','h','k','r'],
  ['i','f','l','v']
]

Return

1	["eat","oath"]

.思路：给words建立一个trie树。然后依次对board中每个点进行dfs，查看组成的单词在不在trie树中。

class Solution {
    class Node{
        Node[] children;
        boolean hasword;
        Node(){
            children = new Node[26];
            hasword = false;
        }
    }
    Node root;
    boolean[][] flag;
    List<String> ans;
    /*插入*/
    public void insert(String key) {
        int index;
        Node e = root;
        for(int i = 0 ; i < key.length() ; i += 1){
            index = key.charAt(i) - 'a';
            if(null == e.children[index]){
                e.children[index] = new Node();
            }
            e = e.children[index];
        }
        e.hasword = true;
    }
    /*对board进行dfs遍历*/
    public void dfs(char[][] board,int i, int j , Node e,String w){
        if(flag[i][j])return;
        int index = board[i][j] - 'a';
        if( null == e.children[index] ){return;}
        w = w+board[i][j];
        if( e.children[index].hasword ){
            ans.add(w);
            e.children[index].hasword = false;
        }
        flag[i][j] = true;
        int[] dx = {-1,0,1,0};
        int[] dy = {0,-1,0,1};
        int x,y;
        for(int q = 0 ; q < dx.length ;  q+=1){
            x = i + dx[q];
            y = j + dy[q];
            if(  x < 0 ||  x >= board.length)continue;
            if(  y < 0 ||  y >= board[i].length )continue;
            dfs(board,x,y,e.children[index],w);

        }
        flag[i][j] = false;


    }
    public List<String> findWords(char[][] board, String[] words) {
        ans = new ArrayList<>();
        if(board.length == 0 || board[0].length == 0 || words.length==0){
            return ans;
        }
        root = new Node();
        flag = new boolean[board.length][board[0].length];
        for(String s : words){
            insert(s);
        }
        for( int i = 0 ; i < board.length ; i += 1 ){
            for( int j = 0 ; j < board[i].length ; j += 1 ){
                dfs(board,i,j,this.root,"");
            }
        }

        return ans;

    }
}

Replace Words

给一个词根表str[] dict = ["cat", "bat", "rat"] ，和一个句子sentence = "the cattle was rattled by the battery"。用词根替换句子为"the cat was rat by the bat"

思路：这道题我一开始是用dfs来做的。但是测试样例太变态了，好长的字符串，导致超时了。这道题只能用循环来做！

这道题有String的两个骚操作：

对String s 的循环

1
2
3

for( char s : s.toCharArray() ){
  System.out.println(s);
}

对多个str的concat：StringBuilder

StringBuilder stringBuilder = new StringBuilder();
for( String e : strs ){
  stringBuilder.append(e);
}
String concatResult = stringBuilder.toString();

代码：

import java.util.ArrayList;
import java.util.List;

/**
 * Created by jiayi on 2017/11/13.
 */

public class TrieTree {

    class Trie{
        class TrieNode{
            TrieNode[] children;
            boolean hasWord;
            TrieNode(){
                children = new TrieNode[26];
                hasWord = false;
            }
        }
        TrieNode root;
        Trie(){
            root = new TrieNode();
        }

        public void insert(String word){
            TrieNode r = this.root;
            int index;
            for( char c: word.toCharArray() ){
                index = c-'a';
                if( null == r.children[index] ){
                    r.children[index] = new TrieNode();
                }
                r = r.children[index];
            }
            r.hasWord = true;
        }
        // 判断树中有没有word的前缀
        public String prefix(String word){
            StringBuilder stringBuilder = new StringBuilder();
            TrieNode r = this.root;
            int idx;
            for( char c : word.toCharArray() ){
                idx = c - 'a';
                if( null != r.children[idx] ){
                    stringBuilder.append(c);
                    if(r.children[idx].hasWord){
                        return stringBuilder.toString();
                    }
                    else{
                        r = r.children[idx];
                    }
                }else{
                    return word;
                }
            }
            return word;
        }
    }

    public String replaceWords(List<String> dict, String sentence) {
        Trie trie = new Trie();
        for(String word : dict){
            trie.insert(word);
        }
        String[] words = sentence.split(" ");
        StringBuilder stringBuilder = new StringBuilder();
        for( String word : words ){
            stringBuilder.append(trie.prefix(word));
            stringBuilder.append(" ");
        }
        return stringBuilder.toString().substring(0,stringBuilder.length()-1);
    }

    public static void main(String[] args){
        String sentence = "a aa a aaaa aaa aaa aaa aaaaaa bbb baba ababa";
        String[] d = {"a", "aa", "aaa", "aaaa"};
        ArrayList<String> dict = new ArrayList<>();
        for(String e : d){
            dict.add(e);
        }
        System.out.println(new TrieTree().replaceWords(dict,sentence));
    }
}

Concatenated Words

给一个str数组。找到其中某些能被其它字符concat而成的单词

用了trie树，beats 93%.简直美滋滋

class Trie{
    class Node{
        boolean hasWord = false;
        Node[] children = new Node[26];
    }
    Node root = new Node();
    private Node newNode(Node root, char c){
        if(root.children[c - 'a'] == null)
            root.children[c - 'a'] = new Node();
        return root.children[c - 'a'];
    }
    public void add(String s){
        Node e = newNode(root, s.charAt(0));
        for(int i = 1; i < s.length(); ++i){
            e = newNode(e, s.charAt(i));
        }
        e.hasWord = true;
    }
    private int canBeConcat(String s, int idx){
        if(idx >= s.length())return 1;
        Node e = root;
        for(int i = idx; i < s.length(); ++i){
            char c = s.charAt(i);
            if(e.children[c - 'a'] == null) return 0;
            if(e.children[c -'a'].hasWord) {
                if(i == s.length() - 1) return 1;
                int next = canBeConcat(s, i + 1);
                if (next > 0) return next + 1;
            }
            e = e.children[c-'a'];
        }
        return 0;
    }
}

public List<String> findAllConcatenatedWordsInADict(String[] words) {
    Trie trie = new Trie();
    for(String str : words){
        if(str.length() == 0)continue;
        trie.add(str);
    }
    // 查看每个单词是否能被组合
    List<String> result = new LinkedList<>();
    for(String str : words){
        if(str.length() == 0)continue;
        if(trie.canBeConcat(str, 0) >= 2)result.add(str);
    }
    return result;
}

Longest Word in Dictionary

给一个单词表，["w","wo","wor","worl", "world"] 。如果一个单词能被其它单词加一个字符组成，那么这个单词就可以作为候选单词。求所有候选单词中长度的最长的那一个，如果两个候选单词长度相同，那么返回字典顺序比较小的那个。

思路：trie树

class Node{
    Node[] children;
    boolean hasWord;
    Node(){
        children = new Node[26];
        hasWord = false;
    }
    public void setHasWord(boolean hasWord){
        this.hasWord = hasWord;
    }
}
Node dummy = new Node();
{
    dummy.setHasWord(true);
}
public void add(String s){
    Node curr = dummy;
    for(char c : s.toCharArray()){
        if(curr.children[c-'a'] == null){
            curr.children[c-'a'] = new Node();
        }
        curr = curr.children[c-'a'];
    }
    curr.setHasWord(true);
}

public String longestWord(String[] words) {
    for(String s : words){
        add(s);
    }
    // 对trie树进行dfs
    dfs(dummy, new StringBuilder());
    return result;
}
String result = "";
int max = 0;
private void dfs(Node curr, StringBuilder sb){
    if(curr == null || !curr.hasWord) return;
    //System.out.println(sb.toString());
    if(sb.length() > max){
        max = sb.length();
        result = sb.toString();
    }
    for(int i = 0; i < 26; ++i){
        sb.append((char)(i+'a'));
        dfs(curr.children[i], sb);
        sb.delete(sb.length() - 1, sb.length());
    }
}

甲乙小朋友的房子

算法-Trie树

实现