理解动态规划
引入例题:triangle
给一个三角形,找到从上到下最短的路径:
1 2 3 4 5 6 [ [2], [3,4], [6,5,7], [4,1,8,3] ]
最短路径是11 (i.e., 2 + 3 + 5 + 1 = 11).
n = 三角形高度
我们用下面几种方法来思考这个题。
方法1,DFS遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 int n;public int minimumTotal (int [][] triangle) int best = Integer.MAX_VALUE; n = triangle.length; dfs(triangle,0 ,0 ,0 ); return best; } public vid dfs (int [][] triangle,int x,int y,int sum) if ( x == n ){ best = Math.max(best,sum); return ; } dfs( triangle, x+1 , y, sum + triangle[x][y] ); dfs( triangle , x+1 , y+1 , sum + triangle[x][y] ); }
复杂度:\(O(2^n)\)
方法2,分治法
没有best全局变量,更好一些。
1 2 3 4 5 6 7 8 9 10 11 int divideConquer (int x,int y) if ( x == n ){ return 0 ; } return A[x][y] + Math.min( divideConquer(x+1 ,y), divideConquer(x+1 ,y+1 ) ); } divideConquer(0 ,0 );
我们分析一下这个分治的定义:
复杂度:\(2^n\)
方法3,记忆化搜索
我们先回头看一下:
我们发现[x+2,y+1]被调用了两次!
就可以用一张哈希表来存储曾经计算过的[x,y]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int divideConquer (int x,int y) if (x == n){ return 0 ; } if ( hash[x][y] != Integer.MAX_VALUE ){ return hash[x][y]; } hash[x][y] = A[x][y] + Math.min( divideConquer(x+1 ,y), divideConquer(x+1 ,y+1 )); return hash[x][y]; } initialize: hash[*][*] = Integer.MAX_VALUE; answser: divideConqure(0 ,0 );
复杂度:\(n^2\)
解决了重复计算的问题。
记忆化搜索是一种lazy loading模式,需要的时候再去算,算完了存下来。属于自顶向下的计算。
方法4,多重循环
这是一种很勤劳的模式。就是提前算好所需要的一切,然后再返回。例如:
有两种方式,一种是自顶向下,一种是自底向上。
自顶向下
我们先看一下自顶向下。
我们先计算从1到2、3的最短路径,然后计算从1到4/5/6的最短路径。最后从4/5/6中挑一个最小的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 f[i][j]表示从顶出发,走到i,j的最小路径长度 f[0 ][0 ] = A[0 ][0 ] for ( int i = 0 ; i < n ; ++i){f[i][0 ] = f[i-1 ][0 ] + A[i][0 ]; f[i][i] = f[i-1 ][i-1 ] + A[i][i]; } for ( int i = 1 ; i < n ; ++i ){ for (int j = 1 ; j < i ; ++j ){ f[i][j] = Math.min(f[i-1 ][j],f[i-1 ][j-1 ]) + A[i][j]; } } return Math.min(f[n-1 ][0 ],f[n-1 ][1 ],...);
自底向上
接下来看一下自底向上的方式。
我们想要计算1到最底端的最小距离,那就需要知道2和3的。那么就要需要知道4,5,6的。那我们先从4,5,6计算起。属于自底向上的计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 A[][] f[i][j]表示从i,j出发走到最后一层的最小路径长度 for ( int i = 0 ; i < n ; ++i ){ f[n-1 ][i] = A[n-1 ][i]; } for ( int i = n - 2 ; i >= 0 ; --i ){ for (int j = 0 ; j <= i ; ++j){ f[i][j] = Math.min(f[i+1 ][j],f[i+1 ][j+1 ]) + A[i][j]; } } return f[0 ][0 ]
什么时候用DP
三个条件满足其一即有可能 是要用DP:
求极值
判断是否可行
统计方案个数
擅长将\(2^n->n^2\)
什么时候不用DP
三个条件满足其一即有可能 是不用DP:
求所有具体 的方案(输出所有回文串)
输入是集合 (是无序的),而不是序列(求最长连续序列),背包问题是例外
暴力方法的复杂度已经是多项式级别,不擅长\(n^3->n^2\)
DP四要素
状态 :f[][]的含义,最难 !
方程 :状态之间的联系,怎么用小状态算大状态
初始化 :最小状态是什么,起点
答案 :最大状态是什么,终点
VS递归三要素
常见DP
坐标型 15%
序列型 30%
双序列 30%
划分型 10%
背包型 10%
区间型 5%
坐标型(矩阵)DP
特点:小人在按照某种方向跳
状态 :
f[x]:从起点走到坐标x...f[x][y]:从起点走到坐标x,y...
方程 :研究走到x,y这个点之前的这一步
初始化 :起点
答案 :重点
例题1:Minimum Path Sum,64
题目:从左上走到右下最短距离。只能向右向下走。求最小路径
状态: f[x][y] : 从起点走到x,y的最短路径
方程 :f[x][y] = Math.min(f[x-1][y],f[x][y-1]+A[x][y]
初始化 :边界
答案 :f[n][m]
例题2,Unique Paths,62
题目:从左上走到右下。只能向右向下走。求方案个数。
状态 :f[x][y]:从[0,0]出发,到[x,y]的方案总数
方程 :f[x][y] = f[x-1][y] + f[x][y-1](需要强调的是,[x-1,y]和[x,y-1]两种方案不会重叠!)
初始化 :第0行、第0列的边界
答案 :f[n][m]
例题3,Unique Paths II,63
如果路上有障碍,求方案个数。
Knight Probability in Chessboard,688
给一个\(n \times n\) 的棋盘,每次可以走八个方向,如图所示。求从[r,c] 出发走K步之后它还停留在棋盘上的概率。
方法1,暴解
暴解肯定会超时,但是基础思路
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Node int in; int all; Node(int in, int all){ this .in = in; this .all = all; } Node(){} } int [][] direct = {{2 ,1 },{2 ,-1 },{1 ,2 },{1 ,-2 },{-2 ,1 },{-2 ,-1 },{-1 ,2 },{-1 ,-2 }}; private Node helper (int N, int K, int r, int c) if (r < 0 || c < 0 || r >= N || c >= N){ return new Node(0 , (int )Math.pow(8 ,K)); } if (K == 0 ) return new Node(1 , 1 ); Node curr = new Node(); for (int [] dir : direct){ Node next = helper(N, K - 1 , r + dir[0 ], c + dir[1 ]); curr.all += next.all; curr.in += next.in; } return curr; } public double knightProbability (int N, int K, int r, int c) Node res = helper(N, K, r, c); return ((double )res.in) / ((double )res.all); }
其实到最后res.all 都会等于\(8^K\) ,因此只需要记录in的个数即可。
方法2,记忆化搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 int [][] direct = {{2 ,1 },{2 ,-1 },{1 ,2 },{1 ,-2 },{-2 ,1 },{-2 ,-1 },{-1 ,2 },{-1 ,-2 }}; double [][][] memo; private double helper (int N, int K, int r, int c) if (r < 0 || c < 0 || r >= N || c >= N){ return 0 ; } if (memo[r][c][K] >= 0 ) return memo[r][c][K]; if (K == 0 ){ memo[r][c][K] = 1 ; return 1 ; } int curr = 0 ; for (int [] dir : direct){ curr += helper(N, K - 1 , r + dir[0 ], c + dir[1 ]); } memo[r][c][K] = curr; System.out.println(curr); return memo[r][c][K]; } public double knightProbability (int N, int K, int r, int c) memo = new double [N][N][K + 1 ]; for (int i = 0 ; i < N; ++i){ for (int j = 0 ; j < N; ++j){ Arrays.fill(memo[i][j], -1 ); } } double inCount = helper(N, K, r, c); return inCount / Math.pow(8 , K); }
然而即使记忆化搜索,会出现inCount爆了double的情况。我们还是需要想其它办法!——那就不要返回全部的和,每次都返回概率嗷嗷嗷嗷嗷
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 int [][] direct = {{2 ,1 },{2 ,-1 },{1 ,2 },{1 ,-2 },{-2 ,1 },{-2 ,-1 },{-1 ,2 },{-1 ,-2 }};double [][][] memo;private double helper (int N, int K, int r, int c) if (r < 0 || c < 0 || r >= N || c >= N){ return 0 ; } if (memo[r][c][K] >= 0 ) return memo[r][c][K]; if (K == 0 ){ memo[r][c][K] = 1 ; return 1 ; } double curr = 0 ; for (int [] dir : direct){ curr += helper(N, K - 1 , r + dir[0 ], c + dir[1 ]); } memo[r][c][K] = curr/8.0 ; return memo[r][c][K]; } public double knightProbability (int N, int K, int r, int c) memo = new double [N][N][K + 1 ]; for (int i = 0 ; i < N; ++i){ for (int j = 0 ; j < N; ++j){ Arrays.fill(memo[i][j], -1 ); } } return helper(N, K, r, c); }
方法3,DP递推
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 memo[r][c][K] : [r,c]走K步后留在棋盘内的概率 转移方程: memo[r][c][K] += memo[r+dir[0 ]][c+dir[1 ]][K-1 ] memo[r][c][K] = memo[r][c][K]/8 初始化: memo[r][c][0 ] = 1 代码: public double knightProbability (int N, int K, int r, int c) int [][] direct = {{2 ,1 },{2 ,-1 },{1 ,2 },{1 ,-2 },{-2 ,1 },{-2 ,-1 },{-1 ,2 },{-1 ,-2 }}; double [][][] memo = new double [N][N][K + 1 ]; for (int i = 0 ; i < N; ++i){ for (int j = 0 ; j < N; ++j){ memo[i][j][0 ] = 1 ; } } for (int k = 1 ; k <= K; ++k){ for (int i = 0 ; i < N; ++i ){ for (int j = 0 ; j < N; ++j){ for (int [] dir : direct){ int i_new = i + dir[0 ], j_new = j + dir[1 ]; if (i_new < 0 || j_new < 0 || i_new >= N || j_new >= N) continue ; memo[i][j][k] += memo[i_new][j_new][k-1 ]; } memo[i][j][k] /= 8 ; } } } return memo[r][c][K]; }
Out of Boundary paths,576
给一个\(m\times n\) 的棋盘,每次可以走向上下左右四个方向。可以走回头路。求问在N步限制下,有多少种走出棋盘的方法。
这道题与之前的不同之处在于,可以向四个方向走。但限制条件就是最多能走N步。
解法一,暴解
暴力DFS!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 int M=1000000007 ; int [][][] memo; private int helper (int m, int n, int i, int j, int stepRemain) if (i < 0 || i >= m || j < 0 || j >= n)return 1 ; if (stepRemain == 0 ) return 0 ; int [] di = {1 ,0 ,-1 ,0 }; int [] dj = {0 ,1 ,0 ,-1 }; int sum = 0 ; for (int k = 0 ; k < 4 ; ++k){ sum += helper(m, n, i + di[k], j + dj[k], stepRemain - 1 ); sum %= M; } return sum%M; } public int findPaths (int m, int n, int N, int i_in, int j_in) if (i_in < 0 || i_in >= m || j_in < 0 || j_in >= n || N == 0 )return 0 ; return helper(m, n, i_in, j_in,N); }
这种方式最容易想到。(一开始没理清题意,以为不可以成环,但其实可以)
解法二,记忆化搜索
这里的关键点就是,状态不仅由i和j决定,还有stepRemain!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 int M=1000000007 ; int [][][] memo; private int helper (int m, int n, int i, int j, int stepRemain) if (i < 0 || i >= m || j < 0 || j >= n)return 1 ; if (stepRemain == 0 ) return 0 ; if (memo[i][j][stepRemain] >= 0 ) return memo[i][j][stepRemain]; int [] di = {1 ,0 ,-1 ,0 }; int [] dj = {0 ,1 ,0 ,-1 }; int sum = 0 ; for (int k = 0 ; k < 4 ; ++k){ sum += (helper(m, n, i + di[k], j + dj[k], stepRemain - 1 )%M); sum %= M; } memo[i][j][stepRemain] = sum%M; return memo[i][j][stepRemain]; } public int findPaths (int m, int n, int N, int i_in, int j_in) if (i_in < 0 || i_in >= m || j_in < 0 || j_in >= n || N == 0 )return 0 ; memo = new int [m][n][N + 1 ]; for (int a = 0 ; a < m; ++a){ for (int b = 0 ; b < n; ++b){ for (int c = 0 ; c <= N; ++c) memo[a][b][c] = -1 ; } } return helper(m, n, i_in, j_in,N); }
解法三,DP递推
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 状态 memo[i][j][step] : 从[i,j]出发走step步有多少种方式走出去 为了方便起见,我们做以下符号处理: 1. 状态记为memo[i,j][step]2. memo[right][step] 为[i,j]的右边格子出发走step步3. memo[left][step] 、 memo[down][step] 、memo[up][step]同理,分别为左边,下面,上面方程: 当left,right,down,up都没有出边界时: memo[i,j][step] = memo[left][step-1 ] + memo[right][step-1 ] + memo[down][step-1 ] + memo[up][step-1 ] 根据状态我们得知,本次计算需要用到上次计算的step-1 的所有状态,因此最外层循环一定是step依次++ 初始化: step = 1 时,所有边界格子的初始值都为1 ,四个角的初始值为2 ( 含义:边上走1 步到达外面时,走法只有1 种!四个角走1 步到达外面时,走法有2 种)即: for (int i = 0 ; i < m; ++i){ memo[i][0 ][1 ] += 1 ; memo[i][n-1 ][1 ] += 1 ; } for (int j = 0 ; j < n; ++j){ memo[0 ][j][1 ] += 1 ; memo[m-1 ][j][1 ] += 1 ; } 结果 : 因为限制至多走N步,因此结果应该为 sum(memo[i_in][j_in][1 ~N]) 代码: public int findPaths (int m, int n, int N, int i_in, int j_in) if (i_in < 0 || i_in >= m || j_in < 0 || j_in >= n || N == 0 )return 0 ; int M=1000000007 ; int [][][] memo = new int [m][n][N + 1 ]; for (int i = 0 ; i < m; ++i){ memo[i][0 ][1 ] += 1 ; memo[i][n-1 ][1 ] += 1 ; } for (int j = 0 ; j < n; ++j){ memo[0 ][j][1 ] += 1 ; memo[m-1 ][j][1 ] += 1 ; } int [] di = {1 ,0 ,-1 ,0 }; int [] dj = {0 ,1 ,0 ,-1 }; for (int step = 2 ; step <= N; ++step){ for (int i = 0 ; i < m ; ++i){ for (int j = 0 ; j < n ; ++j){ for (int k = 0 ; k < 4 ; ++k){ int i_new = i + di[k], j_new = j + dj[k]; if (i_new < 0 || j_new < 0 || i_new >= m || j_new >= n){ continue ; } memo[i][j][step] += memo[i_new][j_new][step - 1 ]; memo[i][j][step] %= M; } } } } int sum = 0 ; for (int step = 0 ; step <= N; ++step){ sum = (sum + memo[i_in][j_in][step]) % M; } return sum; }
例题4,Climbing Stairs,70
有一个楼梯,一步只能跨1/2步。问从0走到n层有多少层方案。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 f[i] -> i位置有多少种 f[i] = f[i-1 ] + f[i-2 ] public int climbStairs (int n) if ( n <= 2 ) return n; int [] f = new int [n+1 ]; f[1 ] = 1 ; f[2 ] = 2 ; for ( int i = 3 ; i <= n ; ++i ){ f[i] = f[i-1 ] + f[i-2 ]; } return f[n]; }
例题5,Jump Game,55
给一个数组A,A[i]表示在这里时最多可以跳A[i]步。只能向前跳。从数组A的第0位置出发,能不能跳到末尾。
这道题有两种解法,一种是DP,一种是贪心。DP会超时,但是思路非常好。
先介绍DP,这个复杂度是\(O(n^2)\) :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public boolean canJump (int [] nums) if ( nums.length == 0 ) return true ; boolean [] f = new boolean [nums.length]; f[0 ] = true ; int i,j; for ( i = 1 ; i < nums.length ; ++i ){ for ( j = 0 ; j < i ; ++j ){ if ( f[j] && i - j <= nums[j] ){ f[i] = true ; break ; } } } return f[nums.length - 1 ]; }
再介绍贪心的思路,这个复杂度是\(O(n)\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public boolean canJump (int [] A) if (A == null || A.length == 0 ) { return false ; } int global = A[0 ]; for (int i = 1 ; i < A.length; i++) { if (i <= global) { global = Math.max(A[i] + i, global); } } return global >= A.length - 1 ; }
例题6,Jump Game II,45
给一个数组A,A[i]表示在这里时最多可以跳A[i]步。只能向前跳。从数组A的第0位置出发跳槽最后一个位置(假设一定能跳到,问最少的跳的次数。
这道题还是有两个思路,一个DP,一个贪心。我们先介绍一下DP,虽然DP会超时:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public int jump (int [] nums) if ( nums.length == 0 ) return 0 ; int [] f = new int [nums.length]; f[0 ] = 0 ; int i,j; for ( i = 1 ; i < nums.length ; ++i ){ f[i] = Integer.MAX_VALUE; for ( j = 0 ; j < i ; ++j ){ if ( i - j <= nums[j] ){ f[i] = Math.min(f[i],f[j]+1 ); } } } return f[nums.length - 1 ]; }
第二种思路,贪心:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 public int jump (int A[], int n) int ret = 0 ; int last = 0 ; int curr = 0 ; for (int i = 0 ; i < n; ++i) { if (i > last) { last = curr; ++ret; } curr = max(curr, i+A[i]); } return ret; }
例题7,Longest Increasing Subsequence,300
求最长严格递增的子序列(子序列:可以跳着选)
例如给[5,4,1,2,3],最长的LIS就是1,2,3
可以用DP——\(n^2\) ,也可以用二分——\(nlogn\) 。我们先介绍一下DP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 5 ,4 ,1 ,2 ,3 理解为: 5 |---| 4 | |---| 3 | | | 2 |---| | | | 1 |---| | | | |---| | | 5 4 1 2 3 的楼梯,目的是从某个木桩出发,从低到高,看能踩多少个木桩 f[i] : (从任意某个木桩)跳到第i个木桩,最多能踩过多少个桩 方程 :f[i] = max{ f[j] + 1 } , j 必须满足 j < i && nums[j] <= nums[i] 初始化:f[i] = 1 答案: Max(f[0 ],f[1 ],...,[n-1 ]) public int lengthOfLIS (int [] nums) int [] f = new int [nums.length]; int i,j; for ( i = 0 ; i < nums.length ; ++i ){ for ( j = 0 ; j < i ; ++j ){ if ( nums[j] < nums[i] ) { f[i] = Math.max(f[i],f[j]+1 ); } } } j = -1 ; for ( i = 0 ; i < f.length ; ++i ){ j = Math.max(j,f[i]); } return j+1 ; }
接下来我们看看二分这个骚操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 tail[i] -> 长度为i+1 的LIS的【最小】末尾是tail[i] 以nums = [4 ,5 ,6 ,3 ]为例: len = 1 : [4 ], [5 ], [6 ], [3 ] => tails[0 ] = 3 len = 2 : [4 , 5 ], [5 , 6 ] => tails[1 ] = 5 len = 3 : [4 , 5 , 6 ] => tails[2 ] = 6 此时如果后面又来了一个x (1 ) 如果x大于所有tails,那就把这个x放在这个里面,并把长度+1 (2 ) 如果tails[i-1 ] < x <= tails[i], 更新 tails[i] size -> 当前最长序列长度 序[0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ] 以[2 ,1 ,5 ,3 ,6 ,4 ,8 ,9 ,7 ]为例: i = 0 --> x = 2 , tail = [2 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ] -> size = 1 [2 ] --> 子序列 2 i = 1 --> x = 1 , tail = [1 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ] -> size = 1 [2 ,1 ] --> 子序列[1 ] i = 2 --> x = 5 , tail = [1 ,5 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ] -> size = 2 [2 ,1 ,5 ] --> 子序列[1 ,5 ] i = 3 --> x = 3 , tail = [1 ,3 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ] -> size = 2 [2 ,1 ,5 ,3 ] --> 子序列[1 ,3 ] i = 4 --> x = 6 , tail = [1 ,3 ,6 ,0 ,0 ,0 ,0 ,0 ,0 ] -> size = 3 [2 ,1 ,5 ,3 ,6 ] --> 子序列[1 ,3 ,6 ] i = 5 --> x = 4 , tail = [1 ,3 ,4 ,0 ,0 ,0 ,0 ,0 ,0 ] -> size = 3 [2 ,1 ,5 ,3 ,6 ,4 ] --> 子序列[1 ,3 ,4 ] i = 6 --> x = 8 , tail = [1 ,3 ,4 ,8 ,0 ,0 ,0 ,0 ,0 ] -> size = 4 [2 ,1 ,5 ,3 ,6 ,4 ,8 ] --> 子序列[1 ,3 ,4 ,8 ] i = 7 --> x = 9 , tail = [1 ,3 ,4 ,8 ,9 ,0 ,0 ,0 ,0 ] -> size = 4 [2 ,1 ,5 ,3 ,6 ,4 ,8 ,9 ] --> 子序列[1 ,3 ,4 ,8 ,9 ] i = 8 --> x = 7 , tail = [1 ,3 ,4 ,7 ,9 ,0 ,0 ,0 ,0 ] -> size = 4 [2 ,1 ,5 ,3 ,6 ,4 ,8 ,9 ,7 ] --> 子序列[1 ,3 ,4 ,7 ,9 ] public int lengthOfLIS (int [] nums) int [] tails = new int [nums.length]; int size = 0 ; for (int x : nums) { int i = 0 , j = size; while (i != j) { int m = (i + j) / 2 ; if (tails[m] < x) i = m + 1 ; else j = m; } tails[i] = x; if (i == size) ++size; } return size; }
Russian Doll Envelopes,354
俄罗斯套娃信封。给一堆信封pair - [w,h] 。要求如果信封A的宽高都小于B的话,那么A就可以放入B。求这堆信封最多能套多少层。
思路一,DP
这里的DP的注意要点在于,需要想清楚比较的是什么。一开始我就没想明白。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 Comparator cmp = new Comparator<int []>() { @Override public int compare (int [] o1, int [] o2) if (o1[0 ] == o2[0 ]){ return o2[1 ] - o1[1 ]; }else return o1[0 ] - o2[0 ]; } }; public int maxEnvelopes (int [][] envelopes) int max = 0 ; Arrays.sort(envelopes, cmp); int [] v = new int [envelopes.length]; Arrays.fill(v, 1 ); for (int i = 0 ; i < envelopes.length; ++i){ for (int j = 0 ; j < i; ++j){ if (envelopes[i][0 ] > envelopes[j][0 ] && envelopes[i][1 ] > envelopes[j][1 ]){ v[i] = Math.max(v[j] + 1 , v[i]); } } max = Math.max(max, v[i]); } return max; }
思路二,二分优化
首先我们考虑一个简单的情况:
所有信封的长和宽并不重复。
这样我们可以:先对长进行排序,然后对 宽 用二分法求 最长递增子序列(LIS)即可。
时间复杂度为:O(nlogn) 用 DP 解法的话就要 O(N^2)了。接下来,我们来考虑该题的情况,即:存在长或者宽相等的情况。在这种情况下, 一个信封是无法被装入另一个 长/宽 相等的一个信封中的。因此我们这边使用了一个技巧: 仍然先对信封的长进行 从小到大 的排序,当长度相等的时候,对宽度进行 从大到小 的排序。 这边都宽度进行 从大到小 的排序是为了使得:当长度相等时,宽度最大的信封是排在最前面的。 这样就避免了会将长度相等,但是宽度更小的信封装入一个宽度更大的信封中的情况。 比如: [[5,4],[5,5],[6,7],[2,3]], 如果长度相等时,宽度仍然按照 从小到大 的排序的话,结果为:[[2,3],[5,4],[5,5],[6,7]] 就会出现:[5,4] => [5,5],即将 宽4长5 的信封装入 宽5长5 的信封中的情况,而这是错误的。 但是如果长度相等时,将宽度按照 从大到小 的顺序排列的话,结果为:[[2,3],[5,5],[5,4],[6,7]]. 这样就能保证:所有宽度大于前面信封宽度的信封的长度必定是大于之前信封长度的。(比较绕,但是意思相信大家已经理解了) 最后只需要对 信封的宽度 求LIS即可。这边使用了二分查找最小结尾数组的方法。较为巧妙,可以达到 O(nlogn) 的时间复杂度。 只需要这么写:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int maxEnvelopes (int [][] envelopes) if (envelopes == null || envelopes.length == 0 || envelopes[0 ] == null || envelopes[0 ].length != 2 ) return 0 ; Arrays.sort(envelopes, new Comparator<int []>(){ public int compare (int [] arr1, int [] arr2) if (arr1[0 ] == arr2[0 ]) return arr2[1 ] - arr1[1 ]; else return arr1[0 ] - arr2[0 ]; } }); int dp[] = new int [envelopes.length]; int len = 0 ; for (int [] envelope : envelopes){ int index = Arrays.binarySearch(dp, 0 , len, envelope[1 ]); if (index < 0 ) index = -index - 1 ; dp[index] = envelope[1 ]; if (index == len) len++; } return len; }
Number of Longest Increasing Subsequence,673
求一个数组的最长递增子序列的个数
这个题对我来说有点难
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public int findNumberOfLIS (int [] nums) if (nums.length == 0 ) return 0 ; int [] dp = new int [nums.length]; int [] counter = new int [nums.length]; Arrays.fill(dp, 1 ); Arrays.fill(counter,1 ); int maxLength = 0 ; int maxLengthNum = 0 ; for (int i = 0 ; i < nums.length; ++i){ for (int j = 0 ; j < i; ++j){ if (nums[j] >= nums[i]) continue ; if (dp[j] + 1 == dp[i]){ counter[i] += counter[j]; }else if (dp[j] + 1 > dp[i]){ dp[i] = dp[j] + 1 ; counter[i] = counter[j]; } } if (dp[i] > maxLength){ maxLength = dp[i]; maxLengthNum = counter[i]; }else if (dp[i] == maxLength){ maxLengthNum += counter[i]; } } return maxLengthNum; }
Increasing Subsequences
求一个数组的所有递增子序列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 一开始的思路就是用递归 定义<List<List>>result[i]为包含nums[i]的所有递增子序列 <List<List>>result[i+1 ]为包含nums[i+1 ]的所有递增子序列,那么 对于<List<List>>result[i+1 ]中的每个成员<List>element来说: 1. 如果 nums[i] <= element.head , 那么 nums[i] + element 可以作为一个result[i]中的结果2. element 本身也可以作为result[i]中的结果3. nums[i]也可以作为result[i]中的结果需要注意的是,当生成到result[0 ]时,我们只需要的是长度大于1 的结果。因此需要判断一下,如果以上三种情况的某种情况长度小于等于1 ,那么就不加入result[i] 然而这样下去的后果是,如果遇到重复元素,就会生成重复的结果。例如我输入nums = [4 , 7 , 6 , 7 ]。那会得到:[[4 , 7 ], [4 , 6 ], [4 , 7 ], [7 , 7 ], [4 , 7 , 7 ], [6 , 7 ], [4 , 6 , 7 ]] 生成了两个[4 ,7 ] 这个问题想了一下午都没有解决。 看了网上的解法,跟我的不是一个套路。哎。来日重刷此题! ======来日 已在回溯里面解决此题。
Arithmetic Slices
给一个序列。求这个序列有多少个等差数列(至少三个元素才算等差数列)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 int [] times;private int getTimes ( int i ) if ( i < 2 ) return 0 ; if ( times[i] > 0 ){ return times[i]; } times[i] = getTimes(i-1 ) + i - 2 ; return times[i]; } public int numberOfArithmeticSlices (int [] A) int n = A.length; if ( n < 3 )return 0 ; times = new int [n+1 ]; times[3 ] = 1 ; int last = A[1 ] - A[0 ],now; int result = 0 ; int sameCount = 2 ; for ( int i = 2 ; i < n ; ++i ){ now = A[i] - A[i-1 ]; if ( now == last ){ ++sameCount; }else { if ( sameCount >= 3 ){result += getTimes(sameCount);} sameCount = 2 ; last = now; } } if ( sameCount >= 3 ){result += getTimes(sameCount);} return result; }
### Perfect Squares
给一个数字,求它被拆成平方和的最少平方和个数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 状态 f[i] : 数字i被拆成平方和的最少个数 1 ,.....,j*j,.....i方程: f[i] = min ( f[i-j^2 ] + 1 ) 代码: int [] nums;int dp (int number) if ( number <= 1 ){ return number; } if ( nums[number] > 0 ){ return nums[number]; } int a; nums[number] = number; for ( int i = 1 ; i < number ; ++i ){ a = number - i*i; if (a < 0 ){ break ;} if ( a == 0 ){ nums[number] = 1 ; break ; } else { nums[number] = Math.min(nums[number], 1 + dp(a)); } } return nums[number]; } int numSquares (int n) nums = new int [n+1 ]; nums[0 ] = 0 ; nums[1 ] = 1 ; return dp(n); }
Min Cost Climbing Stairs
给一个数组,cost[i] 代表从第i格跳到下一步的花费。每次可以跳1或两格。求从开始(可以从0或1起跳)跳到最后的最小花费。
1 2 3 4 5 6 7 8 9 10 11 12 13 int [] dp;private int helper (int [] cost, int idx) if (idx >= cost.length) return 0 ; if (dp[idx] > 0 )return dp[idx]; dp[idx] = Math.min(helper(cost, idx + 1 ), helper(cost,idx + 2 )) + cost[idx]; return dp[idx]; } public int minCostClimbingStairs (int [] cost) dp = new int [cost.length]; return Math.min(helper(cost,0 ),helper(cost,1 )); }
Decode Ways
给一串数字的字符串,其中1表示A, 2表示B... 求字符串可能的编码方式种类
思路:动态规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 dp[i + 1 ] : 字符串[0 ,i]可能的编码方式 初始化: dp[0 ] = 1 dp[1 ] = s.charAt(0 ) <= '9' ? 1 : 0 ; [0 ,1 ,....,i-1 ,i,i+1 ] 情况1 :只要字符[i+1 ]不等于`0 `,那字符[i+1 ]能够独自编码 情况2 :只要字符[i,i+1 ]小于'26' 且大于'09' ,那字符[i,i+1 ]就能编码 转移方程: dp[i+1 ] = dp[i] + dp[i-1 ]; ↑ ↑ 情况1 成立 情况2 成立时 public int numDecodings (String s) if (s.length() == 0 ) return 0 ; if (s.charAt(0 ) == '0' )return 0 ; int [] dp = new int [s.length() + 1 ]; dp[0 ] = 1 ; dp[1 ] = s.charAt(0 ) <= '9' ? 1 : 0 ; for (int i = 1 ; i < s.length(); ++i){ if (s.charAt(i) == '0' ){ dp[i + 1 ] = 0 ; }else { dp[i + 1 ] = dp[i]; } if (s.charAt(i-1 ) > '0' && (s.charAt(i-1 ) < '2' || (s.charAt(i-1 )=='2' &&s.charAt(i) <= '6' ))){ dp[i + 1 ] += dp[i-1 ]; } if (dp[i+1 ] == 0 )return 0 ; } return dp[s.length()]; }
Decode Ways II
接上题,如果其中有字符*表示1-9。同求字符串可能的编码方式种类
思路:接上题的思路,只需要讨论*即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 public int numDecodings (String s) if (s.length() == 0 ) return s.length(); if (s.charAt(0 ) == '0' )return 0 ; long [] dp = new long [s.length() + 1 ]; dp[0 ] = 1 ; if (s.charAt(0 ) == '*' ) dp[1 ] = 9 ; else dp[1 ] = s.charAt(0 ) <= '9' ? 1 : 0 ; for (int i = 1 ; i < s.length(); ++i){ if (s.charAt(i) == '*' ){ dp[i + 1 ] = 9 *dp[i]; }else if (s.charAt(i) == '0' ){ dp[i + 1 ] = 0 ; }else { dp[i + 1 ] = dp[i]; } if (s.charAt(i) == '*' ){ if (s.charAt(i-1 ) == '*' ){ dp[i + 1 ] += 15 *dp[i-1 ]; }else if (s.charAt(i-1 )=='1' ){ dp[i + 1 ] += 9 *dp[i-1 ]; }else if (s.charAt(i-1 ) == '2' ){ dp[i + 1 ] += 6 *dp[i-1 ]; } }else { if (s.charAt(i-1 ) == '*' ){ if (s.charAt(i) != '0' && s.charAt(i) > '6' ){ dp[i + 1 ] += dp[i-1 ]; }else { dp[i + 1 ] += 2 *dp[i-1 ]; } }else if (s.charAt(i-1 ) > '0' && (s.charAt(i-1 ) < '2' || (s.charAt(i-1 )=='2' &&s.charAt(i) <= '6' ))){ dp[i + 1 ] += dp[i-1 ]; } } if (dp[i+1 ] == 0 )return 0 ; dp[i+1 ] = dp[i+1 ]%1000000007 ; } return (int )(dp[s.length()]%1000000007 ); }
Unique Binary Search Trees
求n个节点能组成多少种二叉树。
思路一,记忆化搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int [] memo;private int helper (int remain) if (remain < 0 ) return 0 ; if (memo[remain] > 0 ) return memo[remain]; if (remain <= 1 )return 1 ; int sum = 0 ; for (int i = 0 ; i < remain; ++i) { sum += helper(remain - i - 1 )*helper(i); } memo[remain] = sum; return sum; } public int numTrees (int n) memo = new int [n + 1 ]; return helper(n); }
思路2,DP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 memo[i] : i个元素能组成多少种二叉树 初始化: memo[0 ] = 1 , memo[1 ] = 1 递推公式: memo[i] = Math.sum( memo[i - q - 1 ] * memo[q] ) , 其中 q = [0 ,i) 含义: i个节点的树 = 左子树为i-q-1 个节点 * 右子树为q个节点 public int numTrees (int n) int []memo = new int [n + 1 ]; memo[0 ] = 1 ; memo[1 ] = 1 ; for (int i = 2 ; i <= n; ++i){ for (int q = 0 ; q < i; ++q){ memo[i] += memo[i-q-1 ] * memo[q]; } } return memo[n]; }
Integer Break
给一个数字n,将它分解为n = a + b + .... 的形式,且a*b*... 的乘积最大。求这个最大乘积。
一开始的思路就是递归,但事实上,递归有缺点:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 int max = 0 ; int [] memo; int n; private void helper (int m, int product) if (m <= 1 ){ max = Math.max(max, product); return ; } if (product < memo[m]) return ; memo[m] = product; for (int i = 2 ; i <= m && i < n; ++i){ helper(m - i, product*i); } } public int integerBreak (int n) if (n <= 1 ) return 0 ; if (n == 2 ) return 1 ; this .n = n; memo = new int [n + 1 ]; helper(n, 1 ); return max; }
其实递推公式更快些,因为不会出现重复计算:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public int integerBreak (int n) if (n <= 1 ) return 0 ; if (n == 2 ) return 1 ; if (n == 3 ) return 2 ; int [] memo = new int [n + 1 ]; memo[1 ] = 1 ; memo[2 ] = 1 ; for (int i = 3 ; i <= n; ++i){ memo[i] = i; for (int k = 1 ; k < i; ++k){ memo[i] = Math.max(memo[i], k * memo[i-k]); } } return memo[n]; }
通过这道题,我发现其实有时记忆化搜索并没有递推好使。可能是我记忆化搜索的定义有点问题!应该是求剩余m的最大乘积,然后记下来。
Partition Equal Subset Sum
给一个数组。判断这个数组能否被分为两个和相等的数组。
思路:既然数组的两个不相交的部分和相等,那么任意其中一部分的和都等于sum/2(其中sum为数组和)。那么只需要寻找数组的子集中是否存在和为sum/2的子集即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 int [][] memo;private int helper (int [] nums, int idx, int targetSum) if (targetSum == 0 ) return 1 ; if (targetSum < 0 ) return -1 ; if (idx >= nums.length) return -1 ; if (memo[idx][targetSum] != 0 ) return memo[idx][targetSum]; for (int i = idx; i < nums.length; ++i){ if (helper(nums, i + 1 , targetSum - nums[i]) == 1 ) return 1 ; } memo[idx][targetSum] = -1 ; return -1 ; } public boolean canPartition (int [] nums) if (nums.length <= 1 ) return false ; int sum = 0 ; for (int num : nums) sum += num; if (sum % 2 == 1 ) return false ; memo = new int [nums.length][sum/2 + 1 ]; return helper(nums, 0 , sum/2 ) == 1 ; }
状态转移法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public boolean canPartition (int [] nums) if (nums.length <= 1 ) return false ; int sum = 0 ; for (int num : nums) sum += num; if (sum % 2 == 1 ) return false ; sum /= 2 ; boolean [][] memo = new boolean [nums.length][sum + 1 ]; for (int i = 0 ; i < nums.length; ++i){ if (nums[i] > sum) return false ; for (int k = 0 ; k <= i; ++k){ memo[k][nums[i]] = true ; } } for (int i = nums.length - 1 ; i >= 0 ; --i){ for (int j = 1 ; j <= sum; ++j){ if ( i + 1 < nums.length)memo[i][j] = memo[i+1 ][j]; if (i + 1 < nums.length && !memo[i][j] && j-nums[i] > 0 )memo[i][j] = memo[i+1 ][j-nums[i]]; } } return memo[0 ][sum]; }
Partition to K Equal Sum Subsets
上题的follow up : 给一个数组,判断这个数组能否被分成k个和相等的子集。
思路:dfs + 回溯
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 boolean [] visited;int targetOriginal;private boolean helper (int [] nums, int idx, int k, int target) if (target == 0 ){ if (k == 1 ) return true ; return helper(nums, 0 , k - 1 , targetOriginal); } if (target < 0 ) return false ; for (int i = idx; i < nums.length; ++i){ if (visited[i]) continue ; visited[i] = true ; if (helper(nums, i + 1 ,k, target - nums[i]))return true ; visited[i] = false ; } return false ; } public boolean canPartitionKSubsets (int [] nums, int k) int sum = 0 ; for (int num : nums) sum += num; if (sum % k != 0 ) return false ; visited = new boolean [nums.length]; targetOriginal = sum/k; return helper(nums, 0 , k, targetOriginal); }
Largest Divisible Subset
给一个数组,求数组的一个最长集合:集合中每个元素都能互相整除。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public List<Integer> largestDivisibleSubset (int [] nums) if (nums.length == 0 ) return new LinkedList<>(); Arrays.sort(nums); int [] dp = new int [nums.length]; List<Integer>[] memoList = new List[nums.length]; List<Integer> result = null ; int max = 0 ; for (int i = nums.length - 1 ; i >= 0 ; --i){ memoList[i] = new LinkedList<>(); memoList[i].add(nums[i]); dp[i] = 1 ; int longestJdx = -1 ; for (int j = i + 1 ; j < nums.length; ++j){ if (nums[j] % nums[i] == 0 ){ if (dp[j] + 1 > dp[i]){ dp[i] = dp[j] + 1 ; longestJdx = j; } } } if (longestJdx > i){ memoList[i].addAll(memoList[longestJdx]); } if (dp[i] > max){ result = memoList[i]; max = dp[i]; } } return result; }
单序列型动态规划
状态 :f[i]表示前i个 位置/数字/字符,第i个...
1 2 3 4 前i个位置 |-------------| |1 ,2 ,3 ,4 ,...,i|...,n |-------------|
方程 :f[i] = f[j]...,j是i之前的一个位置
初始化 :f[0]...
答案 :f[n]...
一般answer是f[n]而不是f[n-1]:因为对于n个字符,包含前0个字符(空串)、前1个字符、...、前n个字符
因此f[]一般都要开n+1个
例题1,Word Break
给一个词lintcode,和一个字典dict=["lint","code"],这个词能不能被词拆分成词典中的词→lint code
暴力方法:递归搜索复杂度→\(2^n\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 状态:f[i]表示前i个字符能不能被切成dict中的词 ^表示字符串开始 idx → 0 1 2 3 4 5 6 7 8 f → 1 0 0 0 1 0 0 0 1 ← 1 =true ,0 =false s → ^ l i n t c o d e 计算步骤: i = 4 ,lint: lin + t -> × li + nt -> × l + int -> × '' + lint -> √i = 8 ,lintcode: lintcod + e lintco + de lintc + ode lint + code -> √ f[0 ] = true ; |=======前i个位置=======| |------------|---------| |1 ,2 ,......,j|j+1 ,...,i| |------------|---------| 在j位置切一刀,如果1 ~j能被完美切分,那1 ~i就取决于j+1 ~j能不能被完美切分 for ( int i = 1 ; i <= n ; ++i ){ for ( int j = 1 ; j < i ; ++j ){ if (f[j] && s[j~i] in dict ){ f[i] = true ; break ; } } }
时间复杂度:\(O(n^3)\)
优化
利用单词平均长度(单词不会很长)-- L ,从后往前哇!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 i = 4 ,lint: '' + lint -> √i = 8 ,lintcode: l + intcode li + ntcode lin + tcode lint + code -> √ for ( int i = 1 ; i <= n ; ++i ){ for ( int j = i-1 ; j >= 0 ; --j ){ if (f[j] && s[j~i] in dict ){ f[i] = true ; break ; } } } n:词长度 m:词典单词个数 L:单词平均长度
时间复杂度:\(O(n\times L^2 + m)\)
最终我采用的方案是:用trie给dict建树,搜索时从后往前搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 class Node Node[] children; boolean hasWord; Node(){ children = new Node[26 ]; hasWord = false ; } } class Trie Node root; Trie(){ root = new Node(); } public void add (String s) Node r = this .root; int index; for ( char c : s.toCharArray() ){ index = c - 'a' ; if (null == r.children[index]){ r.children[index] = new Node(); } r = r.children[index]; } r.hasWord = true ; } public boolean search (char [] s,int start,int end) Node r = this .root; int index,count = 0 ; for (int i = start ; i < end ; ++i ){ index = s[i] - 'a' ; if ( null == r.children[index] ){ return false ; }else { r = r.children[index]; ++count; } } boolean res = count == end - start && r.hasWord; return res; } } public boolean wordBreak (String s, List<String> wordDict) char [] c = s.toCharArray(); int n = c.length; Trie trie = new Trie(); for ( String w : wordDict ){ trie.add(w); } boolean [] f = new boolean [n+1 ]; f[0 ] = true ; int i,j; for ( i = 1 ; i <= n ; ++i ){ for ( j = i ; j >= 0 ; --j ){ if ( f[j] && trie.search(c,j,i) ){ f[i] = true ; break ; } } } return f[n]; }
例题2,Palindrome Partitioning II
一个str最少被切割几次可以切割为都是回文串
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 f[i]:前i个字母,最少被切割几次可以切割为都是回文串 |=======前i个位置=======| |------------|---------| |1 ,2 ,......,j|j+1 ,...,i| |------------|---------| 找到一个j,使得1 ~j是回文串,且j+1 ~i能被分割为回文串。则f[i] = f[j] + 1 遍历j,使得f[i] = min( f[j] + 1 ) f[0 ] = -1 for ( int i = 1 ; i <= s.length ; ++i ){ f[i] = Integer.MAX_VALUE; for ( int j = 0 ; j < i ; ++j ){ if ( s[j~i] is Palindrome ){ f[i] = Math.min( f[i], f[j] + 1 ) } } } 代码: class Solution int [][] ifPalindrome; int [] min; public int Palindrome (char [] c,int i, int j) if ( ifPalindrome[i][j] > 0 ) { return ifPalindrome[i][j]; } if ( i == j ){ ifPalindrome[i][j] = 1 ; } else if ( c[i] == c[j] ){ if ( j - i < 3 ){ ifPalindrome[i][j] = 1 ; }else { ifPalindrome[i][j] = ifPalindrome[i+1 ][j-1 ] ; } }else { ifPalindrome[i][j] = 2 ; } return ifPalindrome[i][j]; } public int cut (char [] c,int idx, int n) if ( idx >= n ) {return 0 ;} if ( min[idx] > 0 ){ return min[idx];} min[idx] = n; for ( int j = idx ; j < n ; ++j ){ if ( Palindrome(c,idx,j) == 1 ){ min[idx] = Math.min( 1 + cut( c, j+1 , n ), min[idx] ); } } return min[idx]; } public int minCut (String s) int n = s.length(); if ( n <= 1 ) return 0 ; min = new int [n]; ifPalindrome = new int [n][n]; char [] c = s.toCharArray(); int res = cut(c,0 ,n); return res-1 ; } }
另一种思路
1 f[i] : 前i个字符,最少可以被切为几个回文串
优化 :判断i~j是否是回文串
1 2 3 4 5 i,i+1. ........,j-1 ,j 是回文串,则 i,i+1 ,........,j-1 是回文串 这是一种区间型DP,或者说是一种递推
Palindromic Substrings
输出一个字符串所有的回文子串的个数。
1 2 3 Input: "aaa" Output: 6 Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
我的思路非常暴力:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 1. str -> char [] c2. 定义int [][] ifPalindromic -> ifPalindromic[i][j] = 1 ->是回文串,2 ->不是3. if c[i] == c[j]{ ifPalindromic = Palindromic[i+1 ][j-1 ]; } 4. else : ifPalindromic[i+1 ][j] = Palindromic(c,i+1 ,j); ifPalindromic[i][j-1 ] = Palindromic(c,i,j-1 ); 代码: private int [][] ifPalindromic;int count = 0 ; private int Palindromic (char [] c, int start, int end) if ( start >= end )return 1 ; if ( ifPalindromic[start][end] > 0 )return ifPalindromic[start][end]; if ( c[start] == c[end] ){ ifPalindromic[start][end] = Palindromic(c,start+1 ,end-1 ); }else { ifPalindromic[start][end] = 2 ; } if (start+1 <end)ifPalindromic[start+1 ][end] = Palindromic(c,start+1 ,end); if (start<end-1 )ifPalindromic[start][end-1 ] = Palindromic(c,start,end-1 ); if ( ifPalindromic[start][end] == 1 ){ ++count; } return ifPalindromic[start][end]; } public int countSubstrings (String s) char [] c = s.toCharArray(); int n = c.length; if (n <= 1 ) return n; ifPalindromic = new int [n][n]; for ( int i = 0 ; i < n ; ++i ){ ifPalindromic[i][i] = 1 ; } Palindromic(c,0 ,n-1 ); return count+n; }
上面这种思路用自底向上的方法为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 若 ,i+1 ,...,j-1 , 是回文串 , 且c[i] == c[j] 则 i,...........,j 是回文串 计算过程为 i是从大到小的 j是从i到n的 因为[i+1 ][...]已经算过了 因此[i][j] = ...[i+1 ][j-1 ]肯定能算出来 public int countSubstrings (String s) int n = s.length(); int res = 0 ; boolean [][] dp = new boolean [n][n]; for (int i = n - 1 ; i >= 0 ; i--) { for (int j = i; j < n; j++) { dp[i][j] = s.charAt(i) == s.charAt(j) && (j - i < 3 || dp[i + 1 ][j - 1 ]); if (dp[i][j]) ++res; } } return res; }
其实还有一种更暴力,更简单的解法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int count = 0 ; public int countSubstrings (String s) if (s == null || s.length() == 0 ) return 0 ; for (int i = 0 ; i < s.length(); i++) { extendPalindrome(s, i, i); extendPalindrome(s, i, i + 1 ); } return count; } private void extendPalindrome (String s, int left, int right) while (left >=0 && right < s.length() && s.charAt(left) == s.charAt(right)) { count++; left--; right++; } }
House Robber
给一个数组int[] nums,表示每个商店的价值。要抢劫,但抢劫时必须至少隔一个商铺抢。问能抢到的最大价值。
1 2 3 4 5 6 7 8 9 10 11 12 13 public int rob (int [] nums) if ( nums.length == 0 ) return 0 ; int [] f = new int [nums.length+1 ]; f[0 ] = 0 ; f[1 ] = nums[0 ]; for ( int i = 1 ; i < nums.length ; ++i ){ f[i+1 ] = Math.max(f[i],f[i-1 ]+nums[i]); } return f[nums.length]; }
House Robber II
给一个数组int[] nums,表示每个商店的价值。商店是成环的,即首尾相接。要抢劫,但抢劫时必须至少隔一个商铺抢。问能抢到的最大价值。
1 2 3 4 5 6 7 8 9 [1 ,3 ,4 ,6 ,2 ,5 ] 其实成环的商店如果去掉首/尾某个的话,就不成环了,就变成了上一题。 1 3 5 4 2 6 例如这个环, 假设肯定不抢1 :变成了[3 ,4 ,6 ,2 ,5 ] 假设肯定不抢5 :变成了[1 ,3 ,4 ,6 ,2 ]
House Robber III
商店变成了一个二叉树
思路一,hash表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 HashMap<TreeNode, int []> memo = new HashMap<>(); private int dfs (TreeNode root, boolean robed) if (root == null ) return 0 ; if (!memo.containsKey(root)){ memo.put(root, new int [2 ]); memo.get(root)[0 ] = dfs(root.left, false ) + dfs(root.right, false ); memo.get(root)[1 ] = root.val + dfs(root.left, true ) + dfs(root.right, true ); } if (robed){ return memo.get(root)[0 ]; }else { return Math.max(memo.get(root)[0 ], memo.get(root)[1 ]); } } public int rob (TreeNode root) return Math.max(dfs(root, true ), dfs(root, false )); }
思路2,优化
其实只需要用到本状态和上一状态,并不需要hash表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int rob (TreeNode root) if (root == null ) return 0 ; int [] result = help(root); return Math.max(result[0 ], result[1 ]); } private int [] help(TreeNode root) { if (root == null ) { return new int []{0 , 0 }; } int [] left = help(root.left); int [] right = help(root.right); int with = root.val + left[1 ] + right[1 ]; int without = left[0 ] + right[0 ]; with = Math.max(with, without); int [] result = new int []{with, without}; return result; }
Maximal Square
给一个0/1矩阵。找到最大全1方阵,返回方阵元素个数。
1 2 3 4 5 6 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 -> return 4
这道题我使用了一种较笨的方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 count[i][j] : 当前格子的左上角有多少行/列全1 方阵 [i,j] x x x x x x x x x x x x x x x x x x c[i-1 ,j-1 ] x x x x x 1 <- [i,j] 如果 c[i-1 ,j-1 ] == 1 ,那必须是以下这样时,c[i,j] = 1 + 1 = 1 x x x x x x x x x x x x x x x x x x 1 1 x x x 1 1 <- [i,j] 如果 c[i-1 ,j-1 ] == 2 ,那必须是以下这样时,c[i,j] = 1 + 2 = 3 x x x x x x x x x x x x x x 1 x x x 1 1 x x 1 1 1 <- [i,j] 或者这样,c[i,j] = 1 + 1 = 1 x x x x x x x x x x x x x x 0 x x x 1 1 x x 0 1 1 <- [i,j] public int maximalSquare (char [][] matrix) if ( matrix.length == 0 || matrix[0 ].length == 0 )return 0 ; int max = -1 ; int [][] counter = new int [matrix.length][matrix[0 ].length]; int i,j; for ( i = 0 ; i < matrix.length ; ++i ){ counter[i][0 ] = (int ) matrix[i][0 ] - 48 ; max = Math.max(max,counter[i][0 ]); } for ( j = 0 ; j < matrix[0 ].length ; ++j ){ counter[0 ][j] = (int ) matrix[0 ][j] - 48 ; max = Math.max(max,counter[0 ][j]); } int k,q; for ( i = 1 ; i < matrix.length ; ++i ){ for ( j = 1 ; j < matrix[i].length ; ++j ){ if ( matrix[i][j] == '0' ) continue ; counter[i][j] = 1 ; k = counter[i-1 ][j-1 ]; for ( q = 1 ; q <= k ; ++q ){ if ( matrix[i-q][j] != '1' || matrix[i][j-q] !='1' ){ break ; }else { counter[i][j] += 1 ; } } max = Math.max(max, counter[i][j]); } } return max*max; }
事实上,有一种非常非常机智的方法:
1 2 3 4 5 6 7 8 for (int i = 1 ; i < m; i++) { for (int j = 1 ; j < n; j++) { if (matrix[i][j] == '1' ) { size[i][j] = min(size[i - 1 ][j - 1 ], min(size[i - 1 ][j], size[i][j - 1 ])) + 1 ; maxsize = max(maxsize, size[i][j]); } } }
还有一种更机智的方法。由于f[i][j]只和前3个结果相关
1 2 f[i - 1 ][j - 1 ] f[i][j - 1 ] f[i - 1 ][j] f[i][j]
故只需要保留一个2行的数组!!! 列上不能优化,因为2重循环的时候 下列的时候依赖于上列的结果,上列的结果需要保存到计算下列的时候用
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 int ans = 0 ; if (matrix == null || matrix.length == 0 || matrix[0 ].length == 0 ) { return ans; } int n = 2 ; int m = matrix[0 ].length; int [][] f = new int [n][m]; for (int i = 0 ; i < n; i++) { f[i][0 ] = matrix[i][0 ]; ans = Math.max(f[i][0 ], ans); } for (int i = 0 ; i < m; i++) { f[0 ][i] = matrix[0 ][i]; ans = Math.max(f[0 ][i], ans); } for (int i = 1 ; i < matrix.length; i++) { for (int j = 1 ; j < m; j++) { if (matrix[i][j] == 1 ) { f[i%2 ][j] = Math.min(Math.min(f[(i-1 )%2 ][j-1 ], f[i%2 ][j-1 ]), f[(i-1 )%2 ][j]) + 1 ; } else { f[i%2 ][j] = 0 ; } ans = Math.max(ans, f[i%2 ][j]); } } return ans * ans;
Paint House
给一个二维数组cost[][],大小为n×3。其中cost[i][q]表示第i个房子涂上第q种颜色时的造价。一共有3种颜色。要求两个相邻房子不可以同色。求涂色最小造价
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 0 ,1 ,...,|i-1 | i |,..... | | g | | r | b | --------- | g | r | | | b | --------- | b | r | | | g | 如上图所示,涂第i个房子的时候,取决于第i-1 个房子是什么颜色 而第0 ~i个房子的总最小造价,一定是第i个房子涂r/g/b颜色时的最小值 那我们可以假设我们已知第i-1 个房子涂r/g/b时最小造价,就可以推出第i个房子涂r/g/b时最小造价 total[i][q] = Math.min( total[i-1 ][0 ] + cost[i][1 ], total[i-1 ][0 ] + cost[i][2 ], total[i-1 ][1 ] + cost[i][2 ], total[i-1 ][1 ] + cost[i][0 ], total[i-1 ][2 ] + cost[i][0 ], total[i-1 ][2 ] + cost[i][1 ] ) 将上面这个式子换一种形式: total[i][q] = Math.min( Math.min( total[i-1 ][1 ] + cost[i][0 ], --> 第i个房子颜色为0 的min total[i-1 ][2 ] + cost[i][0 ]), Math.min( total[i-1 ][0 ] + cost[i][1 ], --> 第i个房子颜色为1 的min total[i-1 ][2 ] + cost[i][1 ]), --> Math.min( total[i-1 ][0 ] + cost[i][2 ], --> 第i个房子颜色为2 的min total[i-1 ][1 ] + cost[i][2 ]) --> ) 实现: public int minCost (int [][] costs) if ( costs.length == 0 || costs[0 ].length == 0 ) return 0 ; int n = costs.length; int [][] total = new int [n][costs[0 ].length]; for (int q = 0 ; q < 3 ; ++q ){ total[0 ][q] = costs[0 ][q]; } for ( int i = 1 ; i < n ; ++i ){ for (int q = 0 ; q < 3 ; ++q ){ total[i][q] = Integer.MAX_VALUE; } } for ( int i = 1 ; i < n ; ++i ){ for (int q = 0 ; q < 3 ; ++q ){ total[i][q] = Math.min(total[i][q],costs[i][q] + total[i-1 ][(q+1 )%3 ]); total[i][q] = Math.min(total[i][q],costs[i][q] + total[i-1 ][(q+2 )%3 ]); } } n -= 1 ; int res = Math.min(total[n][0 ],total[n][1 ]); res =Math.min(res,total[n][2 ]); return res; }
上面这个空间复杂度是\(O(n)\) ,时间复杂度是\(O(n)\) 。其实还有优化方法,将空间复杂度降为\(O(1)\) :
1 2 3 4 5 6 7 8 9 10 11 12 public int minCost (int [][] costs) if (costs==null ||costs.length==0 ){ return 0 ; } for (int i=1 ; i<costs.length; i++){ costs[i][0 ] += Math.min(costs[i-1 ][1 ],costs[i-1 ][2 ]); costs[i][1 ] += Math.min(costs[i-1 ][0 ],costs[i-1 ][2 ]); costs[i][2 ] += Math.min(costs[i-1 ][1 ],costs[i-1 ][0 ]); } int n = costs.length-1 ; return Math.min(Math.min(costs[n][0 ], costs[n][1 ]), costs[n][2 ]); }
Target Sum
给一个数组和一个target。求数组的每个元素的正、负和等于target的个数。
思路一,递归memo
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int [][] dp; private int helper (int [] nums, int idx, int S, int sum) if (idx == nums.length){ if (S == sum) return 1 ; else return 0 ; } if (dp[idx][1000 +sum] > 0 ) return dp[idx][1000 +sum]; dp[idx][1000 +sum] = helper(nums, idx + 1 , S, sum + nums[idx]) + helper(nums, idx + 1 , S, sum - nums[idx]); return dp[idx][1000 +sum]; } public int findTargetSumWays (int [] nums, int S) dp = new int [nums.length][2001 ]; return helper(nums, 0 , S, 0 ); }
思路2,非递归memo
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int findTargetSumWays (int [] nums, int S) int allSum = 0 ; for (int e : nums) allSum += e; if (S > allSum || S < -allSum)return 0 ; int [][] dp = new int [nums.length + 1 ][2001 ]; dp[0 ][1000 + 0 ] = 1 ; for (int idx = 1 ; idx <= nums.length; ++idx ){ for (int sum = 0 ; sum <2001 ; ++sum){ if (dp[idx-1 ][sum] != 0 && sum + nums[idx-1 ] < 2001 && sum - nums[idx-1 ] < 2001 ) { dp[idx][sum + nums[idx-1 ]] += dp[idx - 1 ][sum]; dp[idx][sum - nums[idx-1 ]] += dp[idx - 1 ][sum]; } } } return dp[nums.length][1000 + S]; }
优化思路2
由于只会用到前一状态的dp。因此可以简化维度:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int findTargetSumWays (int [] nums, int S) int allSum = 0 ; for (int e : nums) allSum += e; if (S > allSum || S < -allSum)return 0 ; int [] last = new int [2001 ]; last[1000 + 0 ] = 1 ; for (int idx = 1 ; idx <= nums.length; ++idx ){ int [] curr = new int [2001 ]; for (int sum = 0 ; sum <2001 ; ++sum){ if (last[sum] != 0 && sum + nums[idx-1 ] < 2001 && sum - nums[idx-1 ] < 2001 ) { curr[sum + nums[idx-1 ]] += last[sum]; curr[sum - nums[idx-1 ]] += last[sum]; } } last = curr; } return last[1000 + S]; }
硬币组合问题
有数量不限的硬币,币值为25分、10分、5分和1分,请编写代码计算n分有几种表示法。
给定一个int n ,请返回n分有几种表示法。保证n小于等于100000,为了防止溢出,请将答案Mod 1000000007。
我一开始的思路复杂度非常高。
看看这个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 链接:https: 来源:牛客网 public int countWays (int n) int A[] = {1 , 5 , 10 , 25 }; int dp[][] = new int [A.length][n + 1 ]; for (int j = 0 ; j <= n; j++) { dp[0 ][j] = 1 ; } for (int i = 1 ; i < A.length; i++) { for (int j = 0 ; j <= n; j++) { int t = j - A[i]; if (t >= 0 ) { dp[i][j] = (dp[i - 1 ][j] + dp[i][t]) % 1000000007 ; } else { dp[i][j] = dp[i - 1 ][j]; } } } return dp[A.length - 1 ][n]; } public int countWays (int n) int dp[] = new int [n + 1 ], i, A[] = {1 , 5 , 10 , 25 }; for (i = 0 , dp[0 ] = 1 ; i < A.length; i++) { for (int j = A[i]; j <= n; j++) { dp[j] = (dp[j] + dp[j - A[i]]) % 1000000007 ; } } return dp[n]; }
双序列动态规划
给了两个串,研究两个串之间的关系
状态 :f[i][j]代表第一个sequence的前i个数字/字符,配上第二个sequence的前j个...
方程 :f[i][j]=研究第i和第j之间的匹配关系
初始化 :f[i][0]和f[0][i]
答案 :f[n][m]
n = s1.length()
m = s2.length()
例题1,Longest Common Subsequence
最长公共子序列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 子问题的概念 例如刚才的longest increasing subsequence问题,先求leet,再求leetcode 这个问题,可以这么考虑: s1 = abcd s2 = acde ab ac ab acd ab acde abc acd abc acde abcd acde 最后要求的是f[abcd][acde] = ? --> f[4 ][4 ] = ? i ↓ abcd... acde... ↑ j 想要计算f[i][j] -> 字符串0 ~i配上字符串0 ~j的LCS是多少? 如果最后一个字符一样,和另一种不一样,是两种情况。 1. 如果不一样,当然不能都扔了。考虑扔掉一个试试。即考虑f[i][j-1 ]或f[i-1 ][j]。即: if a[i-1 ]!=b[j-1 ] f[i][j] = Math.max( f[i-1 ][j], f[i][j-1 ], f[i-1 ][j-1 ]) 2. 如果一样:就把两个都去掉试试(其实也可以去掉一个试试) else : f[i][j] = Math.max( f[i-1 ][j-1 ] + 1 , f[i][j-1 ], f[i-1 ][j] ) return f[n][m]
例题2,Edit Distance
将第一个字符串最少改动,变成第二个字符串
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 s1 = "mart" ; s2 = "karma" ; return 3 f[i][j] : s1的前i个字符配上s2的前j个字符的LCS长度 if 最后一个字符不等: f[i][j] = Math.min( f[i-1 ][j-1 ] + 1 , f[i][j-1 ] + 1 , f[i-1 ][j] + 1 ) else : f[i][j] = Math.min( f[i][j] = f[i-1 ][j-1 ], f[i][j] = f[i][j-1 ] + 1 , f[i][j] = f[i-1 ][j] + 1 ) 初始化: f[i][0 ] = 0 , f[0 ][j] = 0 答案: f[n][m] 代码 public int minDistance (String word1, String word2) char [] c1 = word1.toCharArray(); char [] c2 = word2.toCharArray(); int n1 = c1.length; int n2 = c2.length; ++n1; ++n2; int [][] min = new int [n1][n2]; min[0 ][0 ] = 0 ; for ( int i = 1 ; i < n1 ; ++i ){ min[i][0 ] = i; } for ( int j = 1 ; j < n2; ++j ){ min[0 ][j] = j; } for ( int i = 1 ; i < n1 ; ++i ){ for ( int j = 1 ; j < n2 ; ++j ){ min[i][j] = n2; if ( c1[i-1 ] == c2[j-1 ] ){ min[i][j] = Math.min( min[i-1 ][j-1 ] , Math.min(min[i][j-1 ] + 1 , min[i-1 ][j] + 1 ) ); }else { min[i][j] = Math.min(min[i-1 ][j-1 ] + 1 , Math.min(min[i][j-1 ] + 1 , min[i-1 ][j] + 1 )); } } } return min[n1-1 ][n2-1 ]; }
例题3,Distinct Subsequences
从S="rabbbit"挑出T = "rabbit"有几种挑法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 状态:f[i][j] S的“前i”个字符中选取T的前j个字符,有多少种方案 方程: 最后一位相等: S = rabb ---- i T = rab ---- j f[i][j] = 有几种方案 : 1. f[i-1 ][j-1 ] + 1 S = rab | b T = ra | b 2. f[i-1 ][j] S = rab | b T = rab 最后一位不等: S = rabbbi ---- i T = rab ---- j 直接扔掉S最后一位f[i][j] = f[i-1 ][j] 初始化: f[i][0 ] = 1 f[0 ][j] = 0 ,j>0 答案:f[n][m] 代码: public int numDistinct (String s, String t) char [] cS = s.toCharArray(); char [] cT = t.toCharArray(); int nS = cS.length + 1 ; int nT = cT.length + 1 ; if ( nS == 1 && nT > 1 ) return 0 ; if ( nT == 1 ) return 1 ; int [][] num = new int [nS][nT]; num[0 ][0 ] = 1 ; for ( int i = 1 ; i < nS; ++i ){ num[i][0 ] = 1 ; } for ( int j = 1 ; j < nT ; ++j ){ num[0 ][j] = 0 ; } for ( int i = 1 ; i < nS ; ++i ){ for ( int j = 1 ; j < nT ; ++j ){ if ( cS[i-1 ] == cT[j-1 ] ){ num[i][j] = num[i-1 ][j-1 ]+ num[i-1 ][j]; }else { num[i][j] = num[i-1 ][j]; } } } return num[nS-1 ][nT-1 ]; }
例题4,Interleaving String
可行性问题
给了三个字符串s1,s2,s3.判断s3是否是由s1和s2交替组成(按顺序,且可交替着挑)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 s1 = "aabcc" ,s2 = "dbbca" s3 = "aadbbcbcac" - > true s3 = "aadbbbaccc" -> false 直观想法 f[i][j][k] -- s1的前i个和s2的前j个 能不能交替组成s3的前k个 k=i+j 即f[i][j][i+j] --> f[i][j] 倒过来看 s1 = ab......i s2 = db......j s3 = aa......k f[i][j] = 如果s1[i]不等于s3[i+j]: f[i-1 ][j] && s1[i-1 ] == s3[i+j-1 ] 或者 如果s2[j]不等于s3[i+j]: f[i][j-1 ] && s2[j-1 ] == s3[i+j-1 ] 否则的话,就不行了! 初始化: f[i][0 ] = ( s[0. ...i-1 ] == s3[0. ..i-1 ] ) f[0 ][j] = ( s2[0. ..j-1 ] == s3[0. ..j-1 ] ) 答案: f[n][m] n = s1.size m = s2.size 代码: public boolean isInterleave (String s1, String s2, String s3) char [] c1 = s1.toCharArray(), c2 = s2.toCharArray(), c3 = s3.toCharArray(); int n1 = c1.length, n2 = c2.length, n3 = c3.length; if ( n3 != n1 + n2 ) return false ; ++n1;++n2;++n3; boolean [][] dp = new boolean [n1][n2]; dp[0 ][0 ] = true ; for ( int i = 1 ; i < n1 ; ++i ){ dp[i][0 ] = c1[i-1 ] == c3[i-1 ] && dp[i-1 ][0 ]; } for ( int j = 1 ; j < n2 ; ++j ){ dp[0 ][j] = c2[j-1 ] == c3[j-1 ] && dp[0 ][j-1 ]; } for ( int i = 1 ; i < n1 ; ++i ){ for ( int j = 1 ; j < n2; ++j ){ if ( c1[i-1 ] == c3[i + j - 1 ] ){ dp[i][j] = dp[i-1 ][j]; } if ( c2[j-1 ] == c3[i + j - 1 ] ){ dp[i][j] = dp[i][j-1 ] || dp[i][j]; } } } return dp[n1-1 ][n2-1 ]; }
Dungeon Game
英雄救美:给一个矩阵int[][] dungegon,每个格子正数代表能量加成,负数代表减弱能量。英雄要从左上走到右下,要求每一时刻英雄的能量不低于1.问英雄初始时最少需要多少能量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 private int go (int i, int j, int [] direct, int [][] dungeon,int [][] init) int initNow; if (dungeon[i][j] > init[i+direct[0 ]][j+direct[1 ]]){ initNow = 1 ; }else { initNow = init[i+direct[0 ]][j+direct[1 ]] - dungeon[i][j]; initNow = Math.max(initNow,1 ); } return initNow; } public int calculateMinimumHP (int [][] dungeon) if (dungeon.length == 0 || dungeon[0 ].length == 0 )return 0 ; int n = dungeon.length;int m = dungeon[0 ].length; int [][] init = new int [n][m]; if (dungeon[n-1 ][m-1 ] > 0 ){ init[n-1 ][m-1 ] = 1 ; }else { init[n-1 ][m-1 ] = -dungeon[n-1 ][m-1 ] + 1 ; } int [] right = {0 ,1 }; int [] down = {1 ,0 }; for (int i = n - 2 ; i >= 0 ; --i){ init[i][m-1 ] = go(i,m-1 ,down,dungeon,init); } for (int j = m - 2 ; j >= 0 ; --j){ init[n-1 ][j] = go(n-1 ,j,right,dungeon,init); } for (int i = n - 2 ; i >= 0 ; --i){ for (int j = m - 2 ; j >= 0 ; --j){ int rightInit = go(i,j,right,dungeon,init); int downInit = go(i,j,down,dungeon,init); init[i][j] = Math.min(rightInit,downInit); } } return init[0 ][0 ]; }
Maximum Length of Repeated Subarray
求两个数字的最大连续子数组长度
思路:动态规划
一开始想多了,用了一种非常绕弯的方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 int [][] dp;private int helper (int [] A, int [] B, int i, int j) if (i >= A.length || j >= B.length) return 0 ; if (dp[i][j] > 0 ) return dp[i][j]; if (A[i] == B[j]) dp[i][j] = 1 + helper(A, B, i + 1 , j + 1 ); else dp[i][j] = 0 ; return dp[i][j]; } public int findLength (int [] A, int [] B) if (A.length == 0 || B.length == 0 ) return 0 ; dp = new int [A.length][B.length]; int globalMAX = 0 ; for (int i = 0 ; i < A.length; ++i){ for (int j = 0 ; j < B.length; ++j){ if (A[i] == B[j]){ globalMAX = Math.max(globalMAX, helper(A, B, i ,j)); } } } return globalMAX; }
实际上,我写的实在是太绕了。我们看一下正确的DP打开方式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int findLength (int [] A, int [] B) if (A.length == 0 || B.length == 0 ) return 0 ; int max = 0 ; int [][] dp = new int [A.length][B.length]; dp[0 ][0 ] = A[0 ] == B[0 ] ? 1 : 0 ; for (int i = 1 ; i < A.length; ++i){ dp[i][0 ] = A[i] == B[0 ] ? 1 : 0 ; for (int j = 1 ; j < B.length; ++j){ dp[0 ][j] = A[0 ] == B[j] ? 1 : 0 ; if (A[i] == B[j]) { dp[i][j] = 1 + dp[i - 1 ][j - 1 ]; max = Math.max(dp[i][j], max); } } } return max; }
然而这并不是最快的。
我们看一下骚操作:
其实就是把dp[][]压缩到了一维。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int findLength (int [] A, int [] B) int n=A.length,m=B.length; int [] dp=new int [m+1 ]; int max=0 ; for (int i=1 ;i<=n;i++){ for (int j=m;j>0 ;j--){ if (A[i-1 ]==B[j-1 ]){ dp[j]=dp[j-1 ]+1 ; max=Math.max(max,dp[j]); }else { dp[j]=0 ; } } } return max; }
Wiggle Subsequence
定义Wiggle子序列为:相邻两数的差一定是正负交替的。比如数组[1,7,4,9,2,5] 的相邻两数差是(6,-3,5,-7,3) ,它是正负交替的。因此它是wiggle数组。
给一个数组,求它的最长的wiggle subsequence的长度。
思路一,DP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int wiggleMaxLength (int [] nums) int [] asPeek = new int [nums.length]; int [] asValley = new int [nums.length]; Arrays.fill(asPeek, 1 ); Arrays.fill(asValley, 1 ); int maxLength = 0 ; for (int i = nums.length - 1 ; i >= 0 ; --i){ for (int j = i + 1 ; j < nums.length; ++j){ if (nums[i] == nums[j]) continue ; if (nums[i] > nums[j]){ asPeek[i] = Math.max(1 + asValley[j], asPeek[i]); }else { asValley[i] = Math.max(1 + asPeek[j], asValley[i]); } } maxLength = Math.max(asPeek[i], maxLength); maxLength = Math.max(asValley[i], maxLength); } return maxLength; }
用DP其实多余了。其实有更快的方式:
思路二,贪心
1 2 3 4 5 6 7 8 9 public int wiggleMaxLength (int [] nums) if (nums==null || nums.length==0 ) return 0 ;int p=1 , q=1 ;for (int i=1 ; i<nums.length; i++){ if (nums[i]>nums[i-1 ]) p=q+1 ; else if (nums[i]<nums[i-1 ]) q=p+1 ; } return Math.min(nums.length, Math.max(p, q)); }
Freedom Trail
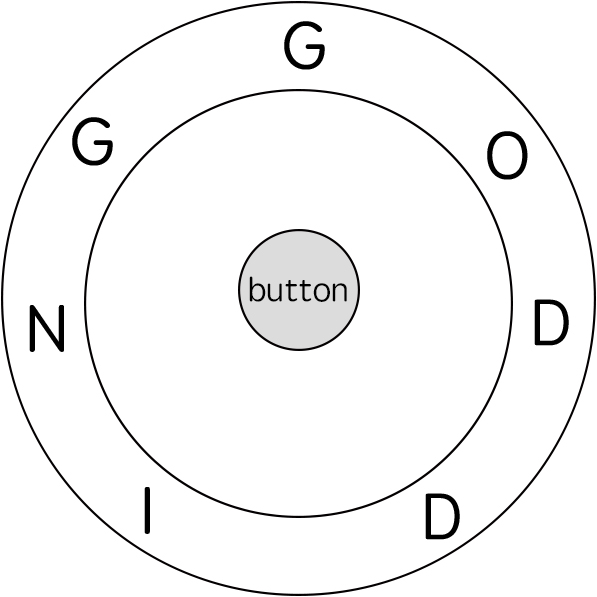
给一个环形字符串ring,代表一个表盘。再给一个字符串key。当ring的十二点钟方向与key的某个字符一样时,可以按下button,表示匹配了这个字符。匹配完事儿之后可以将ring顺时针或逆时针旋转。其中将旋转一个字符记一次操作,且按下button记一次操作。求能够将key匹配完毕时的最少操作次数。
img
分析:
按下button的操作次数恒等于key的长度。
顺时针旋转与逆时针旋转具有等效性,即顺时针旋转k步,等于逆时针旋转ring.length - k 步
思路一,暴解
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 private int helper (String ring, String key, int ring_idx, int key_idx) if (key_idx == key.length()){ return 0 ; } int min_rotated = Integer.MAX_VALUE; for ( int i = ring_idx; i < ring.length() + ring_idx; ++i){ if (ring.charAt(i % ring.length()) == key.charAt(key_idx)){ int roated_curr = i - ring_idx; roated_curr = Math.min(roated_curr, ring.length() - roated_curr); min_rotated = Math.min(min_rotated, roated_curr + helper(ring, key, i% ring.length(), key_idx + 1 )); } } return min_rotated; } public int findRotateSteps (String ring, String key) return helper(ring, key, 0 , 0 ) + key.length(); }
暴解肯定是超时的。
思路2,记忆化搜索
同一个[ring_idx, key_idx] 是调用了多次helper()函数的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 int [][] memo;private int helper (String ring, String key, int ring_idx, int key_idx) if (key_idx == key.length()){ return 0 ; } if (memo[ring_idx][key_idx] > 0 ) return memo[ring_idx][key_idx]; int roated_curr =0 ; int min_rotated = Integer.MAX_VALUE; for ( int i = ring_idx; i < ring.length() + ring_idx; ++i){ if (ring.charAt(i % ring.length()) == key.charAt(key_idx)){ roated_curr = i - ring_idx; roated_curr = Math.min(roated_curr, ring.length() - roated_curr); min_rotated = Math.min(min_rotated, roated_curr + helper(ring, key, i% ring.length(), key_idx + 1 )); } } memo[ring_idx][key_idx] = min_rotated; return min_rotated; } public int findRotateSteps (String ring, String key) min = Integer.MAX_VALUE; memo = new int [ring.length()][key.length()]; return helper(ring, key, 0 , 0 ) + key.length(); }
思路3,DP递推
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 n = ring.length m = key.length 状态: memo[i][j] : ring的[i,n] 与 key的[j,m] 匹配上的最少旋转次数 转移方程: memo[i][j] = Math.min(memo[q][j+1 ] + (i到q所需的旋转次数)) , q = i,i+1 ,...,n+i,且ring[q%n] == key[j] 初始化: j = m - 1 时,memo[i][j] = Math.min(i到q所需的旋转次数) 返回值 memo[0 ][0 ] public int findRotateSteps (String ring, String key) int n = ring.length(); int m = key.length(); int [][] memo = new int [n+1 ][m+1 ]; int min= Integer.MAX_VALUE; int i = 0 ; for (int j = m - 1 ; j >= 0 ; --j){ for (i = 0 ; i < n; ++i) { min = Integer.MAX_VALUE; for (int q = i; q < i + n; ++q) { if (ring.charAt(q % n) != key.charAt(j)) continue ; int rotate = q - i; rotate = Math.min(rotate, n - rotate); int min_curr = j < m - 1 ? memo[q % n][j + 1 ] + rotate : rotate; if (min > min_curr) {min = min_curr;} } memo[i][j] = min; } } return memo[0 ][0 ] + key.length(); }
滚动数组
动态规划四要素:
滚动数组优化是什么?
就是将f[i] = max(f[i-1], f[i-2] + A[i]) 转化为:
f[i%2] = max(f[i - 1] % 2) ,f[(i-2) % 2]
例题1,House Robber
例如给一个数组[3,8,4]。每个元素代表这个房子里的钱。一个强盗想抢钱,但绝对不可以同时抢相邻两个房子里的钱。要怎么抢才能抢到的总钱数最多?
方法一,序列型DP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 f[i] : 前i个房子的最大价值是f[i] 转移方程: 第i个房子有两个状态,抢和不抢 不抢i : = f[i-1 ] 抢i : = f[i-2 ] + A[i] 因此转移方程: f[i] = max(f[i-1 ], f[i-2 ] + A[i]) 初始化: f[0 ] = 0 , f[1 ] = A[0 ] 答案:f[n] public long houseRobber (int [] A) int n = A.length; if (n == 0 ) return 0 ; int [] f = new int [n + 1 ]; f[0 ] = 0 ; f[1 ] = A[0 ]; for (int i = 2 ; i <= n; ++i){ f[i] = Math.max(f[i-1 ], f[i-2 ] + A[i]); } return f[n]; }
方法二,滚动数组优化
1 2 3 4 5 6 7 因为f[i] 只与f[i-1 ] 和 f[i-2 ] 有关,因此只需要记录前两个值!!! 因此可以将f[] 缩小为长度为2 的数组即可 因此转移方程: f[i%2 ] = max(f[(i-1 )%2 ], f[(i-2 )%2 ] + A[i]) 核心:滚动啊滚动!不需要再次更新状态啊!
例题2,House Robber II
给一个数组[3,6,4] 。这个数组是首位相接的。在这个环上怎么抢才能抢的最多?
方法一,拆分数组
1 由于首位相接,因此首位只可以选择其中一个,或者两个都不选!这样就转化成了house robber 1
方法二,copy一份
copy一份变成[3,6,4,3,6,4] 。。但是时间复杂度比较高
例题3,Maximal Square
二维滚动数组问题。
给一个数组 。找到一个最大的全为1的正方形。
普通枚举
1 2 3 4 5 6 7 8 9 10 11 12 int [][] = {{1 ,1 ,1 ,0 },{0 ,0 ,0 ,0 },{0 ,0 ,1 ,1 },{0 ,0 ,1 ,1 }}for (x = 0 -> n){ for (y = 0 -> n){ for (a = 1 -> n){ } } }
复杂度\(O(n^5)\) 。太大了
优化:记忆化搜索
对于一个有效点(值为1)[i,j] ,如果要计算它的左上角最长能延伸的长度,需要考虑三点:
以[i-1, j-1] 为右下角的最大的矩形是多少
以[i,j-1] 为右边界的最大矩形是多少
以[i-1, j] 为下边界的最大矩形是多少
那么:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 因此令 f[i][j]表示以[i,j] 为右下角的正方形的最大边长 left[i][j] : 以[i,j]为右边界的最大矩形 up[i][j] : 以[i,j]为下边界的最大矩形 转移方程: if (maxtrix[i][j] == 1 ){ f[i][j] = max(f[i-1 ][j-1 ], up[i-1 ][j], left[i][j-1 ]) + 1 ; }else { f[i][j] = 0 ; } } 上面的方法除了维护f之外,还需要维护up和left数组,其实可以直接用f来代替up和left。 if (matrix[i][j] == 1 ){ f[i][j] = max(f[i-1 ],[j-1 ],f[i-1 ][j],f[i][j-1 ])+1 } if (matrix[i][j] == 0 ){ f[i][j] = 0 ; } 初始化: f[i][0 ] = matrix[i][0 ] f[0 ][j] = matrix[0 ][j] 答案: max(f[i][j])
滚动数组优化
对于每一个元素(i,j),只与它前一行和前一列的元素有关,与其前两行的元素无关,因此可以对其行进行滚动数组优化。因此转移方程变为:
1 2 3 4 5 6 if (matrix[i][j] == 1 ){ f[i%2 ][j] = max(f[(i-1 )%2 ],[j-1 ],f[(i-1 )%2 ][j],f[i%2 ][j-1 ])+1 } if (matrix[i][j] == 0 ){ f[i%2 ][j] = 0 ; }
习题
Unique Paths
Minimum Path Sum
Edit Distance
记忆化搜索
例题1,Stone Game
给一些石头[3,4,5,6]。每次能合并相邻两个石子,并且花销为两个石子的val和。求把所有石头合并后的总共最小花销是多少。
错误方法,简单贪心 :如果每次都挑最小的两个?这样不是最优的
一个正确打开方式:搜索所有可能情况:
先探究所有第一次合并的所有可能情况:
再探究所有可能情况。自上而下找到所有的最小花费。
换一种思路,自大往小考虑
对于[3,4,5,6]来说,要找到一个[0,3]区间的最小花费问题;
拆分问题:也就是[0,i) 和 [i, 3] 这两个区间的合并问题;子区间有三种情况:
只有1个元素,不需要合并了,耗费为0
只有2个元素,直接合并即可
有k个元素,继续拆分即可
这种倒着搜索的时间复杂度其实跟正着搜索是一样的。但是这里面有区间的重复,也就是可以用记忆化搜索!太机智了!
转移方程:
dp[low][high] = dp[low][i] + dp[i+1][high] + sum[low][high] : 合并左边花销 + 合并右边花销 + 本次合并花销
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public int stoneGame (int [] A) if (A == null || A.length == 0 ) return 0 ; int n = A.length; int [][] f = new int [n][n]; int [][] visit = new int [n][n]; for (int i = 0 ; i < n; ++i){f[i][i] = 0 ;} int [][] sum = new int [n][n]; for (int i = 0 ; i < n; ++i){ sum[i][i] = A[i]; for (int j = i + 1 ; j < n; ++j){ sum[i][j] = sum[i][j-1 ] + A[j]; } } return search(0 , n - 1 , f, visit, sum); } private int search (int l, int r, int [][] f, int [][] visit, int [][] sum) if (visit[l][r] == 1 ) return f[l][r]; if (l == r) return f[l][r]; f[l][r] = Integer.MAX_VALUE; for (int k = l; k < r; ++k){ f[l][r] = Math.min(f[l][r], search(l, k, f, visit, sum) + search(k+1 , r, f, vist, sum) + sum[l][r]); } visit[l][r] = 1 ; return f[l][r]; }
例题2,Burst Ballon
给一个数组[4,1,5,10] 代表每个气球的分值。打爆第i个气球时得到的分数为:当前未打爆的相邻两边的两个气球和自己的价值乘积。求最终能得到的最大价值
震惊,这道题居然和stone game差不多。我们从后往前分析:
定义:dp[0,n]代表把这个区间的气球全部打爆能获得的最大价值
那么倒数第二次被打爆的气球就有可能是(0,n)区间的任意一个,天了噜,太巧妙了
状态转移:dp[i][j] = max(dp[i][k-1] + dp[k+1][j] + midValue) 。 由于dp[i,j] 代表区间[i,j]全部打爆后的最大价值而k是最后一个打爆的,因此midValue = arr[i-1] * arr[k] * arr[j+1]
初始化:dp[i][i] = arr[i]
给一些商品的价格和需要购买的商品总数。有些商品优惠组合可以优惠购买套装。求以最少的价格刚好购买所需的商品。
思路:dfs。
注意的点:HashMap还可以有List
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 Map<List<Integer>, Integer> memo = new HashMap<>(); private int helper (List<Integer> price, List<List<Integer>> special, List<Integer> needs) if (memo.containsKey(needs)) return memo.get(needs); int buyAllCost = 0 ; int i = 0 ; for (i = 0 ; i < needs.size(); ++i){ buyAllCost += needs.get(i) * price.get(i); } int buyOffter = Integer.MAX_VALUE; for (List<Integer> sp : special){ List<Integer> needsCopy = new ArrayList<>(needs); for (i = 0 ; i < needsCopy.size(); ++i){ if (sp.get(i) > needsCopy.get(i))break ; needsCopy.set(i,needsCopy.get(i) - sp.get(i)); } if (i == needsCopy.size()) { buyOffter = Math.min(buyOffter,sp.get(sp.size()-1 ) + helper(price, special, needsCopy)); } } memo.put(needs, Math.min(buyAllCost, buyOffter)); return Math.min(buyAllCost, buyOffter); }
博弈DP
例题1,Coins in a line == Nim Game
直线上有一排硬币。两个人轮流取,每次只能取一个或者两个。最后一个取到棋子的人获胜。问第一个取棋子的人是否有可能获胜?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 画搜索树,以4 个coin为例 先手层: 4T 1 ↙ ↘2 后手层: 3F 2T 1 ↙ ↘2 1 ↙ ↘2 先手层: 2T 1T 1T 0F 搜索树中的TorF表示当前选择coin的选手的输赢 因为两个选手都会选择对自己最为有利的方式选取硬币,因此假设两个选手在开始的时候就已经绘制了这样的搜索树,以4 枚硬币的情况为例,先手可以选择1 个或者2 个: 1. 选1 个,还剩3 个,此时后手无论选择1 个还是2 个,先手都可以赢2. 选2 个,还剩2 个,此时后手选2 个先手就会输掉比赛所以先手选择对自己最为有利的方式,选择1 个,赢得比赛。 由此可见,当前有n个coin的情况下, 该选手是否能够赢得比赛与在剩余n-1 和n-2 枚硬币的情况下对手是否能够赢得比赛有关。 以f(i)表示在剩余i枚硬币情况下当前选手是否能够获胜, 则当下层节点中至少有一个为false 时,本层即可获胜 状态转移方程为: f(i) = !f(i-1 )||!f(i-2 ) 初始化:f(1 )=f(2 )=true 答案:f(i) 【超memory】代码: public boolean canWinNim (int n) if (n <= 3 ) return true ; boolean [] canWin = new boolean [n + 1 ]; canWin[0 ] = false ; canWin[1 ] = true ; canWin[2 ] = true ; canWin[3 ] = true ; for (int i = 4 ; i <= n; ++i){ canWin[i] = !canWin[i-1 ] || !canWin[i-2 ] || !canWin[i-3 ]; } return canWin[n]; } 既然超了memory,那我们用滚动数组优化。【可惜优化后还是超时】 震惊!!!! 一句话!!!!就行了!!! return !(n % 4 == 0 );
给定硬币序列,硬币具有价值,两个人轮流选取硬币,每次只能从最左边选1个或者2个获得相应的价值,最终获得价值多的人获胜,问先手能够获胜
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 f[i]:表示还剩i个硬币,当前取硬币的人最后最多取硬币的价值 如果f[i]>所有硬币价值的一半则可以获胜 以[5 ,1 ,2 ,10 ]为例 先手层: [5 ,1 ,2 ,10 ] 1 ↙ ↘2 后手层: [1 ,2 ,10 ] [2 ,10 ] 1 ↙ ↘2 1 ↙ ↘2 先手层: [2 ,10 ] [10 ] [10 ] [] 两个人在选取硬币的时候,会选择给对方留下尽可能少的价值 转移方程为:f[i] = sum[i]- min(f[i-1 ],f[i-2 ]) 初始化: f[1 ] = coins[i-1 ] f[2 ] = coins[i-1 ]+coins[i-2 ] 答案: if dp[n] > sum[coins]/2 public boolean firstWillWin (int [] values) if (values.length <= 2 ) return true ; for (int i = 0 , j = values.length - 1 ; i < j; ++i, --j){ int temp = values[i]; values[i] = values[j]; values[j] = temp; } int [] f = new int [values.length + 1 ]; f[0 ] = 0 ; f[1 ] = values[0 ]; f[2 ] = values[0 ] + values[1 ]; int [] sum = new int [values.length + 1 ]; for (int i = 1 ; i <= values.length; ++i){ sum[i] = sum[i-1 ] + values[i - 1 ]; } for (int i = 3 ; i <= values.length; ++i){ f[i] = sum[i] - Math.min(f[i-1 ], f[i-2 ]); } return f[values.length] > f[values.length - 1 ] || f[values.length] > f[values.length - 2 ]; }
Predict the Winner
给一个数组,代表每个石子的价值。两个人轮流取石子,每次只能从一边拿一个石子。最终拿到最多石子的人获胜。求先手是否可能获得胜利?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public boolean PredictTheWinner (int [] nums) if (nums.length == 0 ) return false ; if (nums.length == 1 ) return true ; if (nums.length == 2 ) return true ; int [] sum = new int [nums.length]; sum[0 ] = nums[0 ]; for (int i = 1 ; i < nums.length; ++i){ sum[i] = sum[i-1 ] + nums[i]; } int [][] dp = new int [nums.length][nums.length]; for (int i = nums.length - 2 ; i >= 0 ; --i){ dp[i][i+1 ] = Math.max(nums[i], nums[i+1 ]); for (int j = i + 2 ; j < nums.length; ++j){ if (i == 0 ){ dp[i][j] = Math.max(sum[j-1 ] - dp[i][j-1 ] + nums[j], sum[j] - sum[i] - dp[i+1 ][j] + nums[i]); }else { dp[i][j] = Math.max(sum[j-1 ] - sum[i-1 ] - dp[i][j-1 ] + nums[j], sum[j] - sum[i] - dp[i+1 ][j] + nums[i]); } } } return dp[0 ][nums.length - 1 ] >= dp[1 ][nums.length - 1 ] || dp[0 ][nums.length - 1 ] >= dp[0 ][nums.length - 2 ]; }
Can I win
1~n个石头。两个人轮流取,可以从剩下的石头里随便拿。直到两人的石头相加大于desiredTotal时,最后一个取石头的人获胜。请问先手有没有可能获胜?
这道题的状态在于随便拿,因此之前的dp方式不可靠了。因此只能直接用暴力的回溯法,判断对方有没有可能赢,如果对方有可能赢,那自己肯定输。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public boolean canIWin (int maxChoosableInteger, int desiredTotal) int sum = (1 +maxChoosableInteger)*maxChoosableInteger/2 ; if (sum < desiredTotal) return false ; if (desiredTotal <= 0 ) return true ; visited = new boolean [maxChoosableInteger + 1 ]; return helper(desiredTotal); } boolean [] visited;HashMap<String, Boolean> map = new HashMap<>(); private boolean helper (int desiredTotal) if (desiredTotal <= 0 ) return false ; String curr = arr2str(); if (map.containsKey(curr)){ return map.get(curr); } for (int i = 1 ; i < visited.length; ++i){ if (visited[i]) continue ; visited[i] = true ; if (!helper(desiredTotal - i)){ map.put(curr, true ); visited[i] = false ; return true ; } visited[i] = false ; } map.put(curr, false ); return false ; } String arr2str () { StringBuilder sb = new StringBuilder(); for (boolean e : visited){ sb.append(e ? "1" : "0" ); } return sb.toString(); }
背包DP
特点:
用值作为dp维度
dp过程就是填写矩阵
可以滚动数组优化
例题1,Back pack
有一些物品[2,3,5,7],每个数字代表每个物品的体积。有一个书包,书包大小为11。求能放的最重的物品。
建立一个矩阵:boolean f[i][s] : 前i个物品,取出后是否能组成和为s!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int backPack (int m, int [] A) boolean [][] dp = new boolean [m + 1 ][A.length + 1 ]; dp[0 ][0 ] = true ; Arrays.fill(dp[0 ], true ); for (int s = 1 ; s < dp.length; ++s){ for (int i = 1 ; i < dp[s].length; ++i){ dp[s][i] = dp[s][i-1 ] || (s >= A[i-1 ] && dp[s-A[i-1 ]][i-1 ]); } } for (int s = dp.length - 1 ; s >= 0 ; --s){ if (dp[s][A.length]) return s; } return 0 ; }
马甲变换——Partition Equal Subset Sum
给一个数组,判断这个数组是否可以分割成两个和相等的子数组。
可以转化为背包问题:数组总和为36,一半为18背包容量为18,用数组中的数字尽量将背包装满
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public boolean canPartition (int [] nums) int sum = 0 ; for (int e : nums) sum += e; if (sum % 2 != 0 ) return false ; sum /= 2 ; boolean [][] dp = new boolean [sum + 1 ][nums.length + 1 ]; Arrays.fill(dp[0 ], true ); for (int i = 1 ; i <= nums.length; ++i){ for (int s = nums[i-1 ]; s < dp.length; ++s){ dp[s][i] = dp[s-nums[i-1 ]][i-1 ] || dp[s][i-1 ]; } } return dp[sum][nums.length]; }
优化
由于只需要用到i-1的状态。因此我们可以减少一个维度:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public boolean canPartition (int [] nums) int sum = 0 ; for (int e : nums) sum += e; if (sum % 2 != 0 ) return false ; sum /= 2 ; boolean [] dp = new boolean [sum + 1 ]; dp[0 ] = true ; for (int i = 1 ; i <= nums.length; ++i){ for (int s = sum; s >= nums[i-1 ]; --s){ dp[s] = dp[s] || dp[s-nums[i-1 ]]; } } return dp[sum]; }
Back pack II
给出n个物品的体积A[i]和其价值V[i],将他们装入一个大小为m的背包,最多能装入的总价值有多大?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public int backPackII (int m, int [] A, int [] V) int [][] dp = new int [m + 1 ][A.length + 1 ]; for (int s = 1 ; s < dp.length; ++s){ for (int i = 1 ; i < dp[s].length; ++i){ if (s >= A[i-1 ]) dp[s][i] = dp[s-A[i-1 ]][i-1 ] + V[i-1 ]; dp[s][i] = Math.max(dp[s][i], dp[s][i-1 ]); } } return dp[m][A.length]; }
Coin Change
给一些硬币[1,2,5]。再给一个总钱数11。求用硬币组成钱数的最少硬币数字(硬币可以多次拿)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int coinChange (int [] coins, int amount) if (amount == 0 ) return 0 ; if (coins.length == 0 ) return -1 ; int [][] dp = new int [amount + 1 ][coins.length + 1 ]; for (int s = 1 ; s < dp.length; ++s){ for (int i = 1 ; i < dp[s].length; ++i){ dp[s][i] = dp[s][i-1 ]; if (s > coins[i-1 ] && dp[s - coins[i-1 ]][i] > 0 ){ dp[s][i] = Math.min(dp[s][i] == 0 ? Integer.MAX_VALUE : dp[s][i],dp[s - coins[i-1 ]][i] + 1 ); }else if (s == coins[i-1 ]){ dp[s][i] = 1 ; } } } return dp[amount][coins.length] == 0 ? -1 : dp[amount][coins.length]; }
Coin Change 2
给一些硬币,再给一个总钱数。求用硬币组成钱的组成个数
方法一
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public int change (int amount, int [] coins) if (amount == 0 ) return 1 ; if (coins.length == 0 ) return 0 ; int [][] dp = new int [amount + 1 ][coins.length + 1 ]; for (int i = 0 ; i < coins.length; ++i){ if (coins[i] < dp.length)dp[coins[i]][i+1 ] = 1 ; } for (int s = 1 ; s < dp.length; ++s){ for (int i = 1 ; i < dp[s].length; ++i){ dp[s][i] += dp[s][i-1 ]; if (s >= coins[i-1 ])dp[s][i] += dp[s - coins[i-1 ]][i]; } } return dp[amount][coins.length]; }
优化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public int change (int amount, int [] coins) if (amount == 0 ) return 1 ; if (coins.length == 0 ) return 0 ; int [] dp = new int [amount + 1 ]; dp[0 ] = 1 ; for (int i = 1 ; i <= coins.length; ++i){ for (int s = coins[i-1 ]; s < dp.length; ++s){ dp[s] += dp[s - coins[i-1 ]]; } } return dp[amount]; }
例题3, K Sum
给一个数组,从中选出k个数字,使得和为target。求有多少种方案?
转化为:背包问题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int kSum (int [] A, int K, int target) int [][][] dp = new int [target + 1 ][K + 1 ][A.length + 1 ]; Arrays.fill(dp[0 ][0 ], 1 ); for (int s = 1 ; s <= target; ++s){ for (int k = 1 ; k <= K; ++k){ for (int i = 1 ; i <= A.length; ++i){ if (s >= A[i-1 ])dp[s][k][i] += dp[s - A[i-1 ]][k-1 ][i-1 ]; dp[s][k][i] += dp[s][k][i-1 ]; } } } return dp[target][K][A.length]; }
Ones and Zeroes
给一个数组,每个元素是一个01字符串。求从数组中最多拿出多少个元素,能组成m个0和n个1;
这道题第一遍没做出来。第二次看的时候,才发现这是背包问题的变种:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 public int findMaxForm (String[] strs, int m, int n) int [][] count = new int [strs.length][2 ]; for (int i = 0 ; i < strs.length; ++i){ count[i] = counter(strs[i]); } int [][][] dp = new int [m + 1 ][n + 1 ][strs.length + 1 ]; for (int zero = 0 ; zero <= m; ++zero){ for (int one = 0 ; one <= n; ++one){ for (int i = 1 ; i <= strs.length; ++i){ dp[zero][one][i] = dp[zero][one][i-1 ]; if (zero >= count[i-1 ][0 ] && one >= count[i-1 ][1 ]){ dp[zero][one][i] = Math.max(dp[zero][one][i], 1 + dp[zero - count[i-1 ][0 ]][one - count[i-1 ][1 ]][i-1 ]); } } } } return dp[m][n][strs.length]; } private int [] counter(String str){ int [] count = new int [2 ]; for (int i = 0 ; i < str.length(); ++i){ if (str.charAt(i) == '0' ){++count[0 ];} else ++count[1 ]; } return count; }
空间优化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public int findMaxForm (String[] strs, int m, int n) int [][] count = new int [strs.length][2 ]; for (int i = 0 ; i < strs.length; ++i){ count[i] = counter(strs[i]); } int [][] dp = new int [m + 1 ][n + 1 ]; for (int i = 1 ; i <= strs.length; ++i){ for (int zero = m; zero >= 0 ; --zero){ for (int one = n; one >= 0 ; --one){ if (zero >= count[i-1 ][0 ] && one >= count[i-1 ][1 ]){ dp[zero][one] = Math.max(dp[zero][one], 1 + dp[zero - count[i-1 ][0 ]][one - count[i-1 ][1 ]]); } } } } return dp[m][n]; } private int [] counter(String str){ int [] count = new int [2 ]; for (int i = 0 ; i < str.length(); ++i){ if (str.charAt(i) == '0' ){++count[0 ];} else ++count[1 ]; } return count; }
相关Leetcode题
Ugly Number
给一个数num,判断它是不是ugly数——它的质因数只能说是2、3、5。
这道题一开始想复杂了,居然先列出了所有比num小的\(2^i3^j5^k\) 的数。以至于代码变成了这样:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 class Solution int [] k2; int [] k3; int [] k5; int k2_num; int k3_num; int k5_num; private int [] setK(int k_num,double loge){ int size = (int )(loge/Math.log(k_num))+2 ; if (k_num==2 ){ k2_num = size; }else if (k_num==3 ){ k3_num = size; }else if (k_num==5 ){ k5_num = size; } int [] k = new int [size]; k[0 ] = 1 ; int i; for ( i = 1 ; i < k.length ; ++i ){ k[i] = k[i-1 ]*k_num; } return k; } private boolean dp (int num) int i2,i3,i5; long re1,re2; for ( i2 = 0 ; i2 < k2_num ; ++i2 ){ for ( i3 = 0 ; i3 < k3_num ; ++i3 ){ re1 = k2[i2] * k3[i3]; if ( re1 > num )continue ; for ( i5 = 0 ; i5 < k5_num ; ++i5 ){ re2 = re1 * k5[i5]; if ( re2 > num )continue ; else if (re2 == num){ return true ; } } } } return false ; } public boolean isUgly (int num) if (num == 0 )return false ; double loge = Math.log(num); k2 = setK(2 ,loge); k3 = setK(3 ,loge); k5 = setK(5 ,loge); return dp(num); } }
但是!其实我只需要判断它能不能被2、3、5整除!!!!!!
1 2 3 4 5 6 7 8 9 10 11 12 public boolean isUgly (int num) if (num<=0 ) return false ; if (num==1 ) return true ; if (num%2 ==0 ) return isUgly(num/2 ); if (num%3 ==0 ) return isUgly(num/3 ); if (num%5 ==0 ) return isUgly(num/5 ); return false ; }
Burst Balloons
这题太恶心了。
给一个数组,代表气球的分值。如果打破第i号气球,那么会获得nums[last]*nums[i]*nums[next] 的分值。其中last和next分别是i相邻、还没有打破的气球。例如Given [3, 1, 5, 8],Return 167
1 2 nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> [] coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
要求能够获得的最大分值
思路:参考
具体就是一种思路的转变。 假设[i...j]中以k,作为分割点。先破k。 那么 [i, k] and [k, j] 并不是互相独立的。因为他们之间还可以交集。 但是,如果假设,k是最后一个破裂的,那么, [i, k] and [k, j] 就是互相独立的了。
真的就是一个假设的转变,and everything changes. 记住这种reverse想法在DP中的应用。
这题简直让我爆炸
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public int maxCoins (int [] numsIn) int [] nums = new int [numsIn.length + 2 ]; nums[0 ] = 1 ; nums[nums.length - 1 ] = 1 ; for (int i = 0 ; i < numsIn.length; ++i){ nums[i+1 ] = numsIn[i]; } int n = nums.length; int [][] dp = new int [n][n]; for (int gap = 2 ; gap < n; ++gap){ for (int low = 0 ; low < n - gap; ++low){ int high = low + gap; for (int i = low + 1 ; i < high; ++i){ dp[low][high] = Math.max(dp[low][high], nums[low]*nums[i]*nums[high] + dp[low][i] + dp[i][high]); } } } return dp[0 ][n-1 ]; }