# 二分查找
给一个已排序的数组,找到target的位置(第一个出现的、最后一个出现的、任意的)位置。如果没有target,返回-1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 target = 5 start end ↓ ↓ index 0 1 2 3 4 5 6 7 8 nums 2 3 5 8 13 21 34 55 89 ====================================== mid = [start + end ] / 2 = 8 /2 = 4 start mid end ↓ ↓ ↓ index 0 1 2 3 4 5 6 7 8 nums 2 3 5 8 13 21 34 55 89 nums[mid] > target -> target一定在左边 --> end = mid ====================================== mid = [start + end ] / 2 = 4 /2 = 2 start mid end ↓ ↓ ↓ index 0 1 2 3 4 5 6 7 8 nums 2 3 5 8 13 21 34 55 89 nums[mid] == target -> got it ! 复杂度分析 T(n) = T(n/2 ) + O(1 ) 解得 T(n) = O(logn)
用递归还是用while?
递归:好理解,耗费栈空间
while:不好写,但省栈空间,尽量写while
例题
例题1,Binary Search, Leetcode 704
给一个int[] nums,找到target第一次出现的index。没找到就返回-1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 int [] nums = {1 ,2 ,3 ,3 ,4 ,5 ,10 };target = 3 ; return 2 ;模板: int start = 0 ;int end = nums.length - 1 ;int mid;while ( start + 1 < end ){ mid = start + ( end - start )/2 ; if ( nums[mid] == target ){ end = mid; }else if ( nums[mid] < target ){ start = mid; }else if ( nums[mid] > target ){ end = mid; } } if ( nums[start] == target ){ return start; } if ( nums[end] == target ){ return end; } return -1 ;
变体:输出最后一次index
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 mid = [start + end ] / 2 = 8 /2 = 4 start mid end ↓ ↓ ↓ index 0 1 2 3 4 5 6 7 8 nums 3 3 3 3 3 3 3 3 3 由于需要last,所以把start 置为 mid while ( start + 1 < end ) mid = start + ( end - start )/2 ; if ( nums[mid] == target ){ start = mid; }else if ( nums[mid] < target ){ start = mid; }else if ( nums[mid] > target ){ end = mid; } } if ( nums[end] == target ){ return end; } if ( nums[start] == target ){ return start; } return -1 ;
例题2,Search for a range, leetcode 34
给一个int[] nums = {5,7,7,8,8,10],找到target=8出现的范围[3,4]。没找到就返回[-1,-1].
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 思路一,写两个二分,搜两次。先搜start,再搜end 时间复杂度:2log(n) public int [] searchRange(int [] nums, int target) { int [] range = new int [2 ]; range[0 ] = -1 ; range[1 ] = -1 ; if ( nums.length == 0 ) return range; int start = 0 , end = nums.length - 1 ,mid = -1 ,foundIdx = -1 ; while ( start + 1 < end ){ mid = start + ( end - start )/2 ; if ( nums[mid] < target ){ start = mid; }else { end = mid; } } if ( nums[start] == target ){ foundIdx = start; }else if ( nums[end] == target ){ foundIdx = end; } range[0 ] = foundIdx; start = 0 ;end = nums.length - 1 ;mid = -1 ;foundIdx = -1 ; while ( start + 1 < end ){ mid = start + ( end - start )/2 ; if ( nums[mid] <= target ){ start = mid; }else { end = mid; } } if ( nums[end] == target ){ foundIdx = end; }else if ( nums[start] == target ){ foundIdx = start; } range[1 ] = foundIdx; return range; } 思路二,找到后++-- 复杂度O(logn) + O(L) 最坏情况下O(logn) + O(n) public int [] searchRange(int [] nums, int target) { int [] range = new int [2 ]; range[0 ] = -1 ; range[1 ] = -1 ; if ( nums.length == 0 ) return range; int start = 0 , end = nums.length - 1 ,mid = 0 ; boolean found = false ; while ( start + 1 < end ){ mid = start + ( end - start )/2 ; if ( nums[mid] == target ){ found = true ; break ; }else if ( nums[mid] < target ){ start = mid; }else { end = mid; } } if ( nums[start] == target ){ found = true ; mid = start; } if ( nums[end] == target ){ found = true ; mid = end; } if (found == true ) { start = mid - 1 ; end = mid + 1 ; while (start >= 0 && nums[start] == target) { --start; } while (end < nums.length && nums[end] == target) { ++end; } range[0 ] = ++start; range[1 ] = --end; } return range; }
例题3,Search Insert Position, leetcode 35
给一个有序无重数组nums = [1,3,5,6],把target=5插入,问插入的位置=2。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 插入位置 = 第一个大于或等于的位置 (较方便) = 最后一个比它小的位置 方法一: while ( start + 1 < end ){ mid = start + ( end - start )/2 ; if ( nums[mid] == target ){ return mid; }else if ( nums[mid] < target ){ start = mid; }else if ( nums[mid] > target ){ end = mid; } } if ( nums[start] >= target ){ return start; } if ( nums[end] >= target ){ return end; } return end + 1 ; 代码: public int searchInsert (int [] nums, int target) int start = 0 , end = nums.length - 1 ,mid; while ( start + 1 < end ){ mid = start + ( end - start )/2 ; if ( nums[mid] < target ){ start = mid; }else { end = mid; } } if ( target <= nums[start] ){ return start; }else if ( target <= nums[end] ){ return end; }else { return end+1 ; } }
例题4,Search a 2D Matrix, leetcode 74
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 严格递增的Matrix [ [1 ,3 ,5 ,7 ], [10 ,11 ,16 ,20 ], [23 ,30 ,34 ,50 ] ] give target = 3 , return true 思路一:先行后列 思路二:看成一维的 public boolean searchMatrix (int [][] matrix, int target) if ( matrix.length == 0 || matrix[0 ].length == 0 ){ return false ; } int n = matrix.length; int m = matrix[0 ].length; int start = 0 ,end = m * n -1 ,mid,r,c; while ( start + 1 < end ){ mid = start + ( end - start )/2 ; c = mid % m ; r = mid / m ; if ( matrix[r][c] == target ){ return true ; }else if ( matrix[r][c] > target ){ end = mid; }else { start = mid; } } if ( matrix[start/m][start%m] == target ){ return true ; } if ( matrix[end/m][end%m] == target ){ return true ; } return false ; }
例题5,Search a 2D Matrix II, leetcode 240
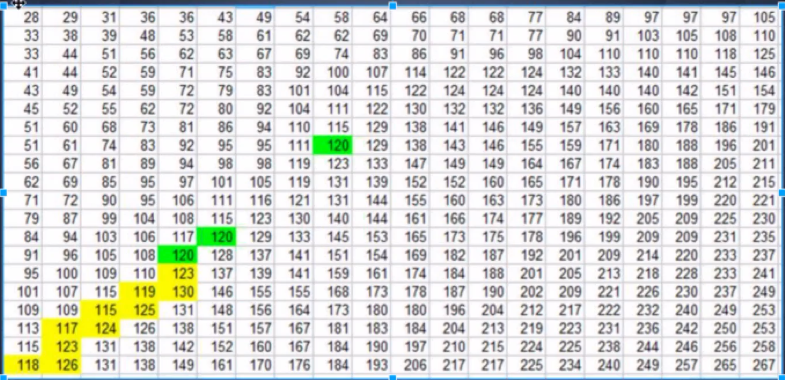
1 2 3 4 5 6 7 8 9 非严格递增 [ [1 ,3 ,5 ,7 ], [2 ,4 ,7 ,8 ], [3 ,5 ,9 ,10 ] ] target = 3 return target出现的次数 = 2
如果这个数比120小,就向右走
如果这个数比120大,就向上走
思路1,每行二分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 private boolean seachRow (int [] arr, int low, int high, int target) int mid; while (low + 1 < high){ mid = low + (high - low)/2 ; if (arr[mid] == target) return true ; if (arr[mid] < target){ low = mid; }else { high = mid; } } if (arr[low] == target || arr[high] == target) return true ; return false ; } public boolean searchMatrix (int [][] matrix, int target) if (matrix.length == 0 || matrix[0 ].length == 0 ) return false ; for (int row = 0 ; row < matrix.length; ++row){ if (target > matrix[row][matrix[0 ].length - 1 ]) continue ; if (seachRow(matrix[row], 0 , matrix[0 ].length - 1 , target)) return true ; } return false ; }
思路2,从左下开始寻找
1 2 3 4 5 6 7 8 9 10 11 12 public boolean searchMatrix (int [][] matrix, int target) if (matrix.length == 0 || matrix[0 ].length == 0 ) return false ; int m = matrix.length, n = matrix[0 ].length; int row = 0 , col = n - 1 ; while (row >= 0 && row < m && col >= 0 && col < n){ if (target == matrix[row][col]) return true ; if (target > matrix[row][col]) {++row;} else {--col;} } return false ; }
例题6,First Bad Version, leetcode 278
代码库的版本号是从 1 到 n 的整数。某一天,有人提交了错误版本的代码,因此造成自身及之后版本的代码在单元测试中均出错。请找出第一个错误的版本号。
你可以通过 isBadVersion 的接口来判断版本号 version 是否在单元测试中出错,具体接口详情和调用方法请见代码的注释部分。
注意事项
请阅读上述代码,对于不同的语言获取正确的调用 isBadVersion 的方法,比如java的调用方式是SVNRepo.isBadVersion(v)
样例
给出 n=5
调用isBadVersion(3),得到false
调用isBadVersion(5),得到true
调用isBadVersion(4),得到true
此时我们可以断定4是第一个错误的版本号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int left = 1 , right = n;while (left < right) { int mid = left + (right - left) / 2 ; if (isBadVersion(mid)) { right = mid; } else { left = mid + 1 ; } } return left; }
例题7,Find Peak Element, leetcode 162
给一个数组。找峰值。相邻两个数都不一样。如果有多个峰值,就随便输出一个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 [1 ,2 ,1 ,3 ,4 ,5 ,7 ,6 ] -> return index 1 or 6 0 1 2 3 4 5 6 7 二分,确定一个mid,找到策略——怎样向左走,怎样向右走 start - left - mid - right - end if left < mid > right -> mid 是峰值else left < mid < right -> 峰值在右边 , start = midelse left > mid > right -> 峰值在左边 , end = midelse left > mid < right -> 两边都有可能 , 随意了代码: int [] nums;private int getNums (int idx) if ( idx < 0 ) return -Integer.MAX_VALUE; if ( idx == nums.length ) return -Integer.MAX_VALUE; return nums[idx]; } public int findPeakElement (int [] nums) this .nums = nums; int start = 0 , end = nums.length - 1 ,mid; while ( start + 1 < end ){ mid = start + ( end - start ) / 2 ; if ( getNums(mid) > getNums(mid-1 )){ if ( getNums(mid) > getNums(mid+1 )){ return mid; }else { start = mid; } }else { end = mid; } } if ( getNums(start) > getNums(end) ){ return start; }else { return end; } }
思考:如果有相邻两个数一样? 就只能\(O(n)\)
Find a Peak Element II, leetcode 1901
给一个二维数组。找相邻峰值。相邻两个数都不一样。如果有多个峰值,就随便输出一个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 class Solution private int getNum (int [][] mat, int row, int col) if (row < 0 || row >= mat.length || col < 0 || col >= mat[0 ].length){ return -1 ; }else { return mat[row][col]; } } public int [] findPeakGrid(int [][] mat) { if (mat.length == 0 || mat[0 ].length == 0 ){ return new int []{0 ,0 }; } int rowStart = 0 , rowEnd = mat.length - 1 ; int colStart = 0 , colEnd = mat[0 ].length - 1 ; int top = 0 , bottom = 0 , left = 0 , right = 0 ; int [] curr = new int [5 ]; while (rowStart <= rowEnd && colStart <= colEnd){ int rowMid = rowStart + (rowEnd - rowStart) / 2 ; int colMid = colStart + (colEnd - colStart) / 2 ; curr[0 ] = getNum(mat, rowMid, colMid); curr[1 ] = getNum(mat, rowMid - 1 , colMid); curr[2 ] = getNum(mat, rowMid + 1 , colMid); curr[3 ] = getNum(mat, rowMid, colMid - 1 ); curr[4 ] = getNum(mat, rowMid, colMid + 1 ); int max = 0 ; for (int i = 1 ; i < curr.length; ++i){ if (curr[i] > curr[max]){ max = i; } } if (rowStart == rowEnd && colStart == colEnd){ return new int []{rowMid, colMid}; } switch (max){ case 0 : return new int []{rowMid, colMid}; case 1 : if (rowEnd == rowStart){ rowStart = rowMid - 1 ; } rowEnd = rowMid - 1 ; break ; case 2 : if (rowEnd == rowStart){ rowEnd = rowMid + 1 ; } rowStart = rowMid + 1 ; break ; case 3 : if (colStart == colEnd){ colStart = rowMid - 1 ; } colEnd = colMid - 1 ; break ; case 4 : if (colStart == colEnd){ colEnd = rowMid + 1 ; } colStart = colMid + 1 ; break ; } } return new int []{0 ,0 }; } }
例题8,Find Minimum in rotated sorted array,153
找有序旋转数组(首位相接)中的最小值。数组中不存在重复元素。
就是在两段上升区间, 找到第一个x。
假设mid在左边的某地方(例如5),那么问题转换为较小区间的原问题--> start = mid
假设mid在右边的某地方(例如1),那么问题转换为较小区间的原问题--> end = mid
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 3 4 5 0 1 2 |-5 -| |-4 -| | |-3 -| | | |-2 -| | | | | |-1 -| | | | | |-0 -| | | ↑ 要它 public int findMin (int [] nums) int start = 0 , end = nums.length - 1 ,mid; if ( nums[start] < nums[end] )return nums[start]; while ( start + 1 < end ){ mid = start + ( end - start ) / 2 ; if ( nums[mid] > nums[start] ){ start = mid; }else { end = mid; } } if ( nums[start] < nums[end] ){ return nums[start]; }else { return nums[end]; } }
例题9,Find Minimum in rotated sorted array II,154
找有序旋转数组(首位相接)中的最小值。数组中可能存在重复元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 4 4 5 6 7 0 1 2 不可以用二分 因为并不确定是向左还是向右走 public int findMin (int [] nums) if ( nums.length == 0 ){ return -1 ; } if ( nums.length == 1 ){ return nums[0 ]; } if ( nums[0 ] < nums[nums.length-1 ] ){ return nums[0 ]; } int i = nums.length - 1 ; while (i > 0 && nums[i-1 ] <= nums[i] ){ --i; } return nums[i]; } 其实也可以用二分! public int findMin (int [] nums) int low = 0 , high = nums.length - 1 ; while (low < high){ int mid = low + (high - low)/2 ; if (nums[low] < nums[high]){ break ; }else { if (nums[mid] < nums[high]){ high = mid; }else if (nums[mid] > nums[low]){ low = mid; }else { ++low; } } } return nums[low]; }
例题10,Search in Rotated Sorted Array,33
从有序旋转数组(首位相接)中找target。数组中不存在重复元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 1. mid在第一段上升区间 if S < T < mid -> end = mid if T > M -> start = end 任然是一个rotated sorted array ... 2. .... public int search (int [] nums, int target) if ( nums.length == 0 ) return -1 ; int start = 0 , end = nums.length - 1 ,mid; while (start + 1 < end){ mid = start + ( end - start ) / 2 ; if ( nums[mid] == target ) return mid; if ( target >= nums[0 ] ) { if ( nums[mid] > nums[0 ] ){ if ( nums[mid] > target ){ end = mid; }else { start = mid; } }else { end = mid; } }else { if ( nums[mid] < nums[0 ] ){ if (nums[mid] > target){ end = mid; }else { start = mid; } }else { start = mid; } } } if ( nums[start] == target ){ return start; } if ( nums[end] == target ){ return end; } return -1 ; }
例题11,Search in Rotated Sorted Array II,81
从有序旋转数组(首位相接)中找target。数组中可能存在重复元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 这题最简单的就是暴力for 循环 还有一种巧妙的二分法: public boolean search (int [] nums, int target) if ( nums.length == 0 ) return false ; int start = 0 , end = nums.length - 1 ,mid; while (start + 1 < end){ mid = start + ( end - start ) / 2 ; if ( nums[mid] == target || target == nums[start]) return true ; if ( nums[mid] == nums[start] ){ ++start ; continue ; } if ( target > nums[0 ] && nums[mid] > nums[0 ] || target < nums[0 ] && nums[mid] < nums[0 ]) { if ( nums[mid] > target ){ end = mid; }else { start = mid; } } else if ( target > nums[0 ] && nums[mid] < nums[0 ]){ end = mid; } else if (target < nums[0 ] && nums[mid] > nums[0 ]){ start = mid; }else { return false ; } } if ( nums[start] == target || nums[end] == target){ return true ; } return false ; }
例题12,Merge Sorted Array
给两个排序数组,将它两合并为一个排序数组。
例题13,Merge Sorted Array II,88
给两个排序数组,A,B,将B合并进A。
思路:从大的入手。
找到两个有序数组的中位数
1 2 3 A = [1 ,2 ,3 ,4 ,5 ,6 ] , B = [2 ,3 ,4 ,5 ] -> median = 3.5 A = [1 ,2 ,3 ] , B = [4 ,5 ] -> median = 3
类似题:find Kth of two Sorted Arrays - 先解决这个
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 A = 1 ,2 ,3 ,4 ,5 ,6 B = 2 ,3 ,4 ,5 最暴力:依次寻找,到K -> O(K) 优化: 先找A的[k/2 ]的数 B的[k/2 ]的数 if A[k/2 ] <= B[k/2 ] A的前k/2 个数都小于【合并后的前K个数】 既然如此,就从A[k/2 + 1 ] & B[0 ]开始找 ,从剩下的里找Top[k - k/2 ] O(logk) ! 震惊! 代码非常复杂。。。 public double findKthSortedArrays (int [] nums1, int [] nums2,int k,int s_n1,int s_n2) if ( s_n1 >= nums1.length ){ return nums2[s_n2 + k]; } if ( s_n2 >= nums2.length ){ return nums1[s_n1 + k]; } if ( k == 0 ){ if ( nums1[s_n1] > nums2[s_n2] ){ return nums2[s_n2]; }else { return nums1[s_n1]; } } if ( k == 1 ){ if ( nums1[s_n1] < nums2[s_n2] ){ return findKthSortedArrays(nums1,nums2,0 ,s_n1+1 ,s_n2); }else { return findKthSortedArrays(nums1,nums2,0 ,s_n1,s_n2+1 ); } } if ( s_n1 + k/2 >= nums1.length && s_n2 + k/2 >= nums2.length ){ if (nums1[nums1.length-1 ] < nums2[nums2.length - 1 ]){ k -= nums1.length - s_n1; s_n1 = nums1.length; }else { k -= nums2.length - s_n2; s_n2 = nums2.length; } } else { if (s_n1 + k / 2 >= nums1.length) { if (nums1[nums1.length - 1 ] < nums2[s_n2 + k / 2 ]) { k -= nums1.length - s_n1; s_n1 = nums1.length; } else { s_n2 += k / 2 ; k -= k/2 ; } } else if (s_n2 + k / 2 >= nums2.length) { if (nums2[nums2.length - 1 ] < nums1[s_n1 + k / 2 ]) { k -= nums2.length - s_n2; s_n2 = nums2.length; } else { s_n1 += k / 2 ; k -= k/2 ; } } else { if (nums1[s_n1 + k / 2 ] > nums2[s_n2 + k / 2 ]) { s_n2 += k / 2 ; } else { s_n1 += k / 2 ; } k -= k / 2 ; } } return findKthSortedArrays(nums1,nums2,k,s_n1,s_n2); } public double findMedianSortedArrays (int [] nums1, int [] nums2) int s_n1 = 0 ,s_n2 = 0 ; int k = (nums1.length + nums2.length); if ( k % 2 == 0 ){ double a = findKthSortedArrays(nums1,nums2,k/2 ,s_n1,s_n2); double b = findKthSortedArrays(nums1,nums2,k/2 -1 ,s_n1,s_n2); return (a+b)/2 ; }else { return findKthSortedArrays(nums1,nums2,k/2 ,s_n1,s_n2); } }
木材加工
把一些木头切成长度相同的小段木头,需要得到的小段的数目至少为 k。计算能够得到的小段木头的最大长度。
例如,有3根木头[232, 124, 456], k=7, 最大长度为114.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public int woodCut (int [] L, int k) int max = 0 ; for (int l : L){ max = Math.max(max, l); } int low = 1 , high = max; while (low + 1 < high){ int mid = low + (high - low) / 2 ; if (can(L, mid, k)) low = mid; else high = mid - 1 ; } if (can(L, high, k)) return high; if (can(L, low, k)) return low; return 0 ; } private boolean can (int [] L, int len, int k) int sum = 0 ; for (int l : L){ sum += l/len; if (sum >= k) return true ; } return sum >= k; }
Guess Number Higher or Lower,Leetcode 374
A出一个1~n之间的数字,B猜为k。每次调用guess(k)时,返回如下几种情况:
B猜得太大了,返回-1
B猜的太小了,返回1
B猜对了,返回0
要求实现一个函数,模拟B猜测数字的过程,最终输出A心里的数字。
思路:二分法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 private int helper (int n, int min, int max) if (min > max) return 0 ; int diff = guess(n); int result = 0 ; if (diff == 0 )return n; else if (diff < 0 ) { result = helper(min + (n - min)/2 ,min, n); if (result > 0 ) return result; } else { result = helper(n + (max - n)/2 , n, max); if (result > 0 ) return result; } return result; } public int guessNumber (int n) return helper(n, 1 , n); }
Valid Perfect Square
判断一个数字是不是平方数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 private boolean helper (int num) int low = 0 , high = num/2 ; int mid; int power; while (low + 1 < high){ mid = low + (high - low)/2 ; power = mid * mid; if (power == num) return true ; if (mid > 46340 || power > num){ high = mid; }else { low = mid; } } if (low*low == num) return true ; if (high*high == num) return true ; return false ; } public boolean isPerfectSquare (int num) if (num == 1 ) return true ; if (num == 0 ) return false ; if (num > 2147399560 ) return false ; if (num == 2147399560 ) return true ; return helper(num); }
Find Right Interval
给一些区间[ [3,4], [2,3], [1,2] ] 。寻找每个区间最近的右邻居
思路:将区间按照start排序,例如start分别是[1,2,3] 。然后依次寻找每个区间的end值是否有稍微比它大一点点的那个数。比如寻找比4大一点的数字,不存在,因此返回-1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 class Node implements Comparable <Node > int start; int idx; Node(int start, int idx){ this .start = start; this .idx = idx; } @Override public int compareTo (Node o) return this .start - o.start; } public String toString () return String.valueOf(start); } } Node[] nodesStart; public int [] findRightInterval(Interval[] intervals) { nodesStart = new Node[intervals.length]; for (int i = 0 ; i < intervals.length; ++i){ nodesStart[i] = new Node(intervals[i].start, i); } Arrays.sort(nodesStart); int [] result = new int [intervals.length]; for (int i = 0 ; i < intervals.length; ++i){ result[i] = findLargerHelper(intervals[i].end); } return result; } private int findLargerHelper (int num) int low = 0 , high = nodesStart.length - 1 ; int mid; while (low + 1 < high){ mid = low + (high - low) / 2 ; if (num == nodesStart[mid].start){ return nodesStart[mid].idx; }else if (num > nodesStart[mid].start){ low = mid; }else { high = mid; } } if (nodesStart[low].start >= num) return nodesStart[low].idx; else if (nodesStart[high].start >= num) return nodesStart[high].idx; else return -1 ; }
Find K Closest Elements
给一个有序数组和一个x。找到离x最近的k个数。
一开始我的思路比较暴力:先找到与x最近的那个数,然后向左向右寻找k个最近的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 public List<Integer> findClosestElements (int [] arr, int k, int x) List<Integer> result = new ArrayList<>(); System.out.println(k); if (k == 0 || arr.length == 0 )return result; int pos = find(arr, x); System.out.println(pos); int low = 0 , high = 0 ; if (pos == -1 ){ low = 0 ; high = k - 1 ; }else { if (pos < arr.length - 1 && x - arr[pos] > arr[pos + 1 ] - x) ++pos; low = pos; high = pos; --k; while (k > 0 && low > 0 && high < arr.length - 1 ){ if (x - arr[low - 1 ] > arr[high + 1 ] - x){ ++high; }else { --low; } --k; } if (k > 0 ){ if (low > 0 ){low = low - k; high = arr.length - 1 ; } else if (high < arr.length) {high = high + k; low = 0 ;} k = 0 ; } } for (int i = low; i <= high; ++i){ result.add(arr[i]); } return result; } private int find (int [] arr, int x) int low = 0 , high = arr.length -1 ; while (low + 1 < high){ int mid = low + (high - low) / 2 ; if (arr[mid] == x)return mid; if (arr[mid] > x){ high = mid; }else { low = mid; } } if (arr[high] <= x)return high; if (arr[low] <= x)return low; return -1 ; }
优化
可以省略向左向右寻找的过程。
对于数1 ... M ... N来说,找到k个最相近与x的数。可以试着先找一个左区间leftBound, 那么[leftBound, leftBound+k]就是要找的值。其中 0 <= leftBound <= N - k
那么对于数1 ... M ...M+k... N-k 来说
如果\(x<M\) ,那么leftBound一定在M的左边;
如果\(M<x<M+k\) 时,即M...x...M+k时,
如果x恰好出现在M和M+k的正中间时,那么M就是要找的左区间
如果x更靠近M+k,那么可以将low跳到M
如果x更靠近M,那么可以将high跳到M
如果\(x >= M+k\) ,那么leftBound一定在M+k的右边
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public List<Integer> findClosestElements (int [] arr, int k, int x) List<Integer> result = new ArrayList<>(); System.out.println(k); if (k == 0 || arr.length == 0 )return result; if (arr.length == 1 ){ result.add(arr[0 ]); return result; } int low = 0 , high = arr.length - k; int mid = 0 ; while (low + 1 < high){ mid = low + (high - low) / 2 ; if (x <= arr[mid]){ high = mid; }else { if (x >= arr[mid + k - 1 ]){ low = mid; } else if (x - arr[mid] > arr[mid + k - 1 ] - x){ low = mid; }else { high = mid; } } } if (high + k <= arr.length && x - arr[low] > arr[high + k - 1 ] - x){ mid = high; }else { mid = low; } for (int i = mid; i < mid + k; ++i){ result.add(arr[i]); } return result; }
Find K-th Smallest Pair Distance
给一个数组[1,3,1] 。返回第k小的数之间的距离
一开始就是暴力\(O(n^2)\) + 堆,然而超时了
桶排序
算出没种dist的次数;然后用桶排序!从小到大扫描,找到合适的桶!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int smallestDistancePair (int [] nums, int k) int [] DistBucket = new int [1000000 ]; for (int i = 0 ; i < nums.length; ++i){ for (int j = i + 1 ; j < nums.length; ++j){ ++DistBucket[Math.abs(nums[j] - nums[i])]; } } for (int i = 0 ; i < DistBucket.length; ++i){ k -= DistBucket[i]; if (k <= 0 ){ return i; } } return -1 ; }
二分法 + DP
骚操作啊
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 public int smallestDistancePair (int [] nums, int k) if (nums.length==0 ) return -1 ; Arrays.sort(nums); int n = nums.length; int high = nums[n - 1 ] - nums[0 ]; int low = high; for (int i = 1 ; i < n; ++i){ low = Math.min(low, nums[i] - nums[i-1 ]); } while (low < high){ int mid = low + (high - low) / 2 ; int count = getCount(nums, mid); if (count >= k){ high = mid; }else { low = mid + 1 ; } } return low; } private int getCount (int [] nums, int mid) int n = nums.length; int i = 0 ; int count = 0 ; for (int j = 1 ; j < n; ++j){ while (nums[j] - nums[i] > mid) ++i; count += (j - i); } return count; }
Kth Smallest Number in Multiplication Table
乘法表中的第k个数
妈蛋啊,二维矩阵啊,行列分别有序啊,二分啊,永远记不住啊