甲乙小朋友的房子

甲乙小朋友很笨，但甲乙小朋友不会放弃

0%

算法-二叉树与分治

发表于 更新于 分类于

一些题目 implement of ....

时间复杂度训练

复习：

\[T(n) = T(\frac{n}{2}) + O(1) → O(logn)\]

\[T(n) = T(\frac{n}{2}) + O(n) → O(n)\]

** 问题1**

通过O(1)的时间,把n的问题,变为了两个n/2的问题,复杂度是多少?

\[T(n) = 2T(\frac{n}{2}) + O(1) → O(n)\]

解决：树型分析法

1
2
3
4
5
6
7
8
9
           n
       /      \      -->  本次拆分耗费了O(1)的时间
     n/2       n/2
    / \        / \   -->  本次拆分耗费了O(2)的时间
n/4   n/4   n/4   n/4
.....................
         第k+1层       -->  本次拆分耗费了O(2^k)的时间
.....................  -->  本次拆分耗费了O(n/2)的时间

总复杂度：

\[O(1+2+4+....+2^k+...+\frac{n}{2})\tag{1}\]

设\(2^m = \frac{n}{2}\)，则\(m=log(\frac{n}{2})=logn-log2=logn\)

则公式（1）等于：

\[O(2^0+2^1+2^2+....+2^{logn})\]

\[=O(\frac{a_1(1-q^n)}{1-q})=O(\frac{1-2^{logn}}{2-1})=O(n)\tag{结果}\]

问题2

\[T(n) = 2T(\frac{n}{2}) + O(n) =?\]

1
2
3
4
5
6
7
8
9
           n
       /      \      -->  本次拆分耗费了O(n)的时间
     n/2       n/2
    / \        / \   -->  本次拆分耗费了O(n)的时间
n/4   n/4   n/4   n/4
.....................
         第k+1层       -->  本次拆分耗费了O(n)的时间
.....................  -->  本次拆分耗费了O(n)的时间

总复杂度：

\[O(n+n+...+n)----logn次 = O(nlog(n))\tag{结果}\]

样例问题：mergeSort，就是这个复杂度！

二叉树的遍历

  • 前序遍历 - 先root
  • 中序遍历-中间是root
  • 后续遍历-最后root

二叉树的三种遍历，均由根节点开始，且路线是一样的，只不过节点访问的顺序不一样 .这条路线从根节点开始，沿着左子树深入下去，当深入到最左端，无法再深入下去返回

刚才深入时遇到的节点，再逐一进入其右子树，进行如此的深入和返回，直到最后从根 的右子树的返回根节点为止

在这一过程中，返回节点的顺序和进入节点的顺序相反，因此即先进入后返回，这一特 性正好符合栈后进先出的特点，因此三种遍历的非递归实现可以借助栈来实现： 在沿着左子树深入时，进入一个节点就将其压栈。

若是先序遍历，则在进栈之前访问之， 当沿左分支深入不下去时，则返回，即从栈中弹出前面压入的节点。

若为中序遍历，则 此时访问该节点，然后从该节点的右子树继续深入；若为后序遍历，则将此节点二次入 栈，然后从该节点的右子树继续深入，与前面类似，仍为进入一个节点入栈一个节点， 深入不下去时返回，直到第二次从栈里弹出该节点，才访问之

非递归实现

整体思路

因为要在遍历完节点的左子树后接着遍历节点的右子树，为了能找到该节点，需要使用栈来进行暂存。中序和后序也都涉及到回溯，所以都需要用到栈。

三道题的解决思路可统一，模板也极其相似：

  1. 将二叉树分为“左”（包括一路向左，经过的所有实际左+根）、“右”（包括实际的右）两种节点
  2. 使用同样的顺序将“左”节点入栈
  3. 从下到上，以此访问其的右子树，同时把右子树看成一颗完整的树，重复上面的步骤

比如{1,2,3}，当cur位于节点1时，1、2属于“左”节点，3属于“右”节点。DFS的非递归实现本质上是在协调入栈、出栈和访问，三种操作的顺序。上述统一使得我们不再需要关注入栈顺序，仅需要关注出栈和访问（第3点），随着更详细的分析，你将更加体会到这种简化带来的好处。

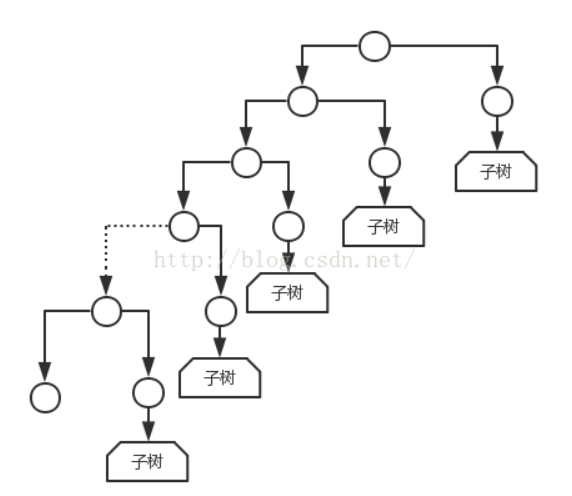
针对上述逻辑我们可以抽象出一个遍历规则，如下图所示：

即上面说到的三个步骤！

  1. 将二叉树分为“左”（包括一路向左，经过的所有实际左+根）、“右”（包括实际的右）两种节点
  2. 使用同样的顺序将“左”节点入栈
  3. 从下到上，以此访问其的右子树，同时把右子树看成一颗完整的树，重复上面的步骤

二叉树的遍历

前序

先序和中序的情况是极其相似的。

  • 先序的实际顺序：【根左】【右】
  • 中序的实际顺序：【左根】【右】

使用上述思路，先序和中序的遍历顺序可统一为：【“左”“右”】。

给我们的直观感觉是代码也会比较相似。实际情况正是如此，先序与中序的区别只在于对“左”节点的访问上。

非递归实现1

不需要入栈，每次遍历到“左”节点，立即输出即可。

需要注意的是，遍历到最左下的节点时，实际上输出的已经不再是实际的根节点，而是实际的左节点。这符合先序的定义。

1
2
3
4
5
while (cur != null) {
    results.add(cur.val);
    stack.push(cur);
    cur = cur.left;
}

而后，因为我们已经访问过所有“左”节点，现在只需要将这些没用的节点出栈，然后转向到“右”节点。于是“右”节点也变成了“左”节点，后续处理同上。

1
2
3
4
5
if (!stack.empty()) {
    cur = stack.pop();
    // 把右子树作为一颗树，重复上面的步骤
    cur = cur.right;
}

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private List<Integer> dfsPreOrder(TreeNode root) {
    List<Integer> results = new ArrayList<>();
    Stack<TreeNode> stack = new Stack<>();

    TreeNode cur = root;
    while (cur != null || !stack.empty()) {
        while (cur != null) {
            results.add(cur.val);
            stack.push(cur);
            cur = cur.left;
        }
        if (!stack.empty()) {
            cur = stack.pop();
            // 把右子树作为一颗树，重复上面的步骤
            cur = cur.right;
        }
    }

    return results;
}

递归实现1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//调用主函数
public ArrayList<Integer> preorderTraversal(TreeNode root){
  ArrayList<Integer> result = new ArrayList<Integer>();
  traverse(root,result);
  return result;
}
//递归定义：把root为根的preorder加入到result里
private void traverse(TreeNode root, ArrayList<Integer> result){
  //停止条件
  if( root == null ){
    return;
  }
  //拆分问题
  result.add(root.val);
  traverse(root.left,result);
  traverse(root.right,result);
}


递归

定义： 把root为根的preorder加入到result里

拆分问题： 放root,放left,放right

停止条件： root == null

递归实现2，分治

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public ArrayList<Integer> preorderTraversal(TreeNode root){
  ArrayList<Integer> result = new ArrayList<Integer>();
  // null or leaf
  if( null == root ){
    return result;
  }
  //分解问题
  ArrayList<Integer> left = preorderTraversal(root.left);
  ArrayList<Integer> right = preorderTraversal(root.right);
  
  //合并问题
  result.add(root.val);
  result.addAll(left);
  result.addAll(right);
  return result;
}

递归可能爆栈！

Binary Tree Preorder Traversal

实现二叉树的前序遍历

这道题除了以上说的递归和非递归的两种方式，还有另一种非递归的实现方式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public List<Integer> preorderTraversal(TreeNode root){
  Stack<TreeNode> stack = new Stack<>();
  list<Integer> preorder = new ArrayList<>();
  if( null == root ){
    return preorder;
  }
  stack.push(root);
  while( !stack.empty() ){
    TreeNode node = stack.pop();
    preorder.add( node.val );
    if( node.right != null ){
      stack.push(node.right);
    }
    if( node.left != null ){
      stack.push(node.left);
    }
  }
  return preorder;
}

Flatten Binary Tree to Linked List

将二叉树按照前序遍历的顺序变为一颗只有右孩子的单链表

方法1，栈

思路：整体思路就是按照前序遍历的方式.

非递归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public void flatten(TreeNode root) {
        if(root == null) return;
        // 其实就是前序遍历
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;
        //stack.push(node);
        TreeNode last = node;

        while (!stack.isEmpty() || node != null){

            while (node != null){
                //System.out.println(node.val);
                if(node.right != null) {
                    stack.push(node.right); // 这里只push进去node.right(因为后期只会使用到node.right)
                }
                if(node.left != null) {// 将左孩子挪到右孩子上
                    node.right = node.left;
                    TreeNode left = node.left;
                    node.left = null;
                    node = left;
                }else {
                    break;
                }
                last = node;
            }
            if(stack.empty()) return;
            node = stack.pop();
            last.right = node; // 当前节点的右孩子应该是上一轮的最后一个孩子
            last = node;
        }
    }

递归的另一种实现

自己写的实在是太糟糕了。我们看看九章的写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
1. 分别将右子树、左子树入栈
2. 本节点的新right就是栈顶的东西哇

public void flatten(TreeNode root) {
        if(root == null) return;
        
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        
        while (!stack.empty()){
            TreeNode node = stack.pop();
            if(node.right != null) stack.push(node.right);
            if(node.left != null) stack.push(node.left);
            
            // 连接
            node.left = null;
            if(stack.empty()) node.right = null;
            else node.right = stack.peek();
        }
    }

方法2，分治

这道题的递归方式我是死活都没写出来。其实就是向右探到底那没想通。哎

假设某节点的左右子树T(root->left)和T(root->right)已经flatten成linked list了：

1
2
3
4
5
6
7
8

  1
/   \
2      5
\       \
 3        6 <- rightLast
   \
    4  <- leftLast

如何将root、T(root->left)、T(root->right) flatten成一整个linked list？显而易见：

1
2
3
4
temp = root.right
root.right  = root.left
root.left = NULL
leftTail.right = temp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public void flatten(TreeNode root) {
    helper(root);
}

// flatten root and return the last node
private TreeNode helper(TreeNode root) {
    if (root == null) {
        return null;
    }
    
    TreeNode leftLast = helper(root.left);
    TreeNode rightLast = helper(root.right);
    
    // connect leftLast to root.right
    if (leftLast != null) {
        leftLast.right = root.right;
        root.right = root.left;
        root.left = null;
    }
    
    if (rightLast != null) {
        return rightLast;
    }
    
    if (leftLast != null) {
        return leftLast;
    }
    
    return root;
}

参考Grandyang

Verify Preorder Serialization of a Binary Tree,331

验证一个序列是否是二叉树的前序遍历。例如给出"9,3,4,#,#,1,#,#,2,#,6,#,#"，它是某一个树（示意图如下）的前序遍历，那就输出true。

1
2
3
4
5
6
7
     _9_
    /   \
   3     2
  / \   / \
 4   1  #  6
/ \ / \   / \
# # # #   # #
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int visitedCount = 0;
int idx = 0;
private void helper(String[] preoders){

    if(idx >= preoders.length) return;
    ++visitedCount;
    // 访问根节点
    //System.out.println(preoders[idx]);
    if(!Character.isDigit(preoders[idx].charAt(0))) return;
    // 访问左节点
    ++idx;
    helper(preoders);
    ++idx;
    // 访问右节点
    helper(preoders);
}

public boolean isValidSerialization(String preorder) {
    String[] preorders = preorder.split(",");
    if(preorders.length == 1 && preorders[0].charAt(0) == '#') return true;
    if(preorders.length % 2 == 0 || preorders.length < 3) return false;
    helper(preorders);
    return visitedCount == preorders.length;
}

中序

基于对先序的分析，先序与中序的区别只在于对“左”节点的处理上，我们调整一行代码即可完成中序遍历。

1
2
3
4
5
6
7
8
9
10
while (cur != null) {
    stack.push(cur);
    cur = cur.left;
}
if (!stack.empty()) {
    cur = stack.pop();
    results.add(cur.val); // 仅调整该行代码
    // 把右子树作为一颗树，重复上面的步骤
    cur = cur.right;
}

注意，我们在出栈之后才访问这个节点。因为先序先访问实际根，后访问实际左，而中序恰好相反。相同的是，访问完根+左子树（先序）或左子树+根（中序）后，都需要转向到“右”节点，使“右”节点称为新的“左”节点。

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private List<Integer> dfsInOrder(TreeNode root) {
     List<Integer> results = new ArrayList<>();
     Stack<TreeNode> stack = new Stack<TreeNode>();

     TreeNode cur = root;
     while (cur != null || !stack.empty()) {
         while (cur != null) {
             stack.push(cur);
             cur = cur.left;
         }
         if (!stack.empty()) {
             cur = stack.pop();
             results.add(cur.val);
             // 把右子树作为一颗树，重复上面的步骤
             cur = cur.right;
         }
     }
     return results;
 }

Binary Tree Inorder Traversal

实现二叉树的中序遍历

Minimum Absolute Difference in BST

给一个二叉搜索树。求任意两个结点之间绝对值的最小值。

思路：中序遍历，用后面的减去前面的，找到最小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int getMinimumDifference(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        int last = -1;
        int min = Integer.MAX_VALUE;
        while (!stack.isEmpty() || null != root){
            while (null != root) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if(last == -1){last = root.val;}
            else{
                min = Math.min(min,root.val - last);
                last = root.val;
            }
            root = root.right;
        }
        return min;
    }

Kth Smallest Element in a BST

输出搜索二叉树第k小的数

BST的中序遍历是从小到大的。因此只需要按照中序遍历输出第k个即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int kthSmallest(TreeNode root, int k) {
        if(null == root) return -1;
        Stack<TreeNode> stack = new Stack<>();
        int i = 0;
        while (!stack.isEmpty() || null != root){
            while (null != root){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            i++;
            if(i == k){
                return root.val;
            }
            root = root.right;
        }
        return -1;
    }

递归写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int count=0;
int ans=0;
int flag=0;
void inorder(TreeNode node,int k){
    if(node==null){
        return ;
    }
    inorder(node.left,k);
    count++;
    ans=node.val;
    if(count==k){
        flag=ans;
    }
    inorder(node.right,k);
}
public int kthSmallest(TreeNode root, int k) {
   inorder(root,k);
    return flag;
}

后序

后序的情况略有不同，但仍然十分简洁。

  • 后序的实际顺序：左右根

入栈顺序不变，我们只需要考虑第3点的变化。出栈的对象一定都是“左”节点（“右”节点会在转向后称为“左”节点，然后入栈），也就是实际的左或根；实际的左可以当做左右子树都为null的根，所以我们只需要分析实际的根。

对于实际的根，需要保证先后访问了左子树、右子树之后，才能访问根。实际的右节点、左节点、根节点都会成为“左”节点入栈，所以我们只需要在出栈之前，将该节点视作实际的根节点，并检查其右子树是否已被访问即可。如果不存在右子树，或右子树已被访问了，那么可以访问根节点，出栈，并不需要转向；如果还没有访问，就转向，使其“右”节点成为“左”节点，等着它先被访问之后，再来访问根节点。

所以，我们需要增加一个标志，记录右子树的访问情况。由于访问根节点前，一定先紧挨着访问了其右子树，所以我们只需要一个标志位。

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public List<Integer> postorderTraversal(TreeNode root) {
    List<Integer> result = new LinkedList<>();
    if (root == null){
        return result;
    }

    Stack<TreeNode> stack = new Stack<TreeNode>();
    HashSet<TreeNode> flag = new HashSet<TreeNode>();
    TreeNode curr = root;
    while (stack.size() > 0 || curr != null){
        while(curr != null){
            stack.push(curr);
            curr = curr.left;
        }

        if (stack.size() > 0){
            curr = stack.peek();
            if (!flag.contains(curr)){
                // 说明curr.right还没有被访问过。所以先不弹出它
                flag.add(curr);
                curr = curr.right;
            }else{
                // 说明curr.right已经被访问过了。那就可以弹出&访问curr了
                result.add(curr.val);
                stack.pop();
                curr = null; // 不需要转向了，继续弹！
            }
        }
    }

    return result;
}

Binary Tree Postorder Traversal,145

实现二叉树的后序遍历

这道题除了以上说的递归和非递归的两种方式，还有一种更骚气的，利用双栈。

但实际上它做的是反向的先序遍历。亦即遍历的顺序是：节点 -> 右子树 -> 左子树。这生成的是后根遍历的逆序输出。使用第二个栈，再执行一次反向输出即可得到所要的结果。

下面是它的实现步骤：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
将根节点压入第一个栈
从第一个栈中弹出一个元素，压入第二个栈
然后分别将该节点的左右孩子压入第一个栈
重复步骤2和步骤3直到第一个栈为空
执行结束，第二个栈中就保存了所有节点的后序遍历输出结果。依次将元素从第二个栈中弹出即可。

public List<Integer> postorderTraversal(TreeNode root) {
  List<Integer> result = new ArrayList<>();
  if (root == null) {
    return result;
  }

  Stack<TreeNode> tmp = new Stack<>();
  Stack<TreeNode> out = new Stack<>();

  tmp.push(root);

  while (!tmp.isEmpty()) {
    TreeNode node = tmp.pop();
    out.push(node);

    if (node.left != null) {
      tmp.push(node.left);
    }

    if (node.right != null) {
      tmp.push(node.right);
    }
  }

  while (!out.isEmpty()) {
    result.add(out.pop().val);
  }
  return result;
}

或者用root->right->left，然后用链表addFirst反转结果 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public List<Integer> postorderTraversal(TreeNode root) {
    LinkedList<Integer> result = new LinkedList<>();
    if (root == null){
        return result;
    }

    Stack<TreeNode> stack = new Stack<TreeNode>();
    TreeNode curr = root;
    while (stack.size() > 0 || curr != null){
        while(curr != null){
            result.addFirst(curr.val);
            stack.push(curr);
            curr = curr.right; // right!
        }

        if (stack.size() > 0){
            curr = stack.pop();
            curr = curr.left; // left!
        }
    }

    return result;
}

Subtree of Another Tree，572

给两个二叉树s和t。判断t是否是s的子树

思路一，非递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
private boolean check(TreeNode s_in,TreeNode t_in){
        TreeNode t = t_in;
        TreeNode s = s_in;
        Stack<TreeNode> stack_t = new Stack<>();
        Stack<TreeNode> stack_s = new Stack<>();
        while (!stack_t.isEmpty()|| null != t){
            while (null != t && null != s){
                stack_t.push(t);
                stack_s.push(s);
                s = s.left;
                t = t.left;
            }
            if(!( (null != t && null != s)||
                    (null == t && null == s)) ) return false;
            t = stack_t.pop();
            s = stack_s.pop();
            if(t.val != s.val){
                return false;
            }
            s = s.right;
            t = t.right;
            if(!( (null != t && null != s)||
                    (null == t && null == s)) ) return false;
        }
        return true;
    }
    public boolean isSubtree(TreeNode s, TreeNode t) {
        // 从s里找t
        // 遍历s
        if(null == t) return true;
        if(null == s) return false;
        Stack<TreeNode> stack = new Stack<>();
        while (!stack.isEmpty() || null != s){
            while (null != s){
                stack.push(s);
                s = s.left;
            }
            s = stack.pop();
            if(s.val == t.val){
                if(check(s,t)) return true;
            }
            s = s.right;
        }
        return false;
    }

思路二，递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public boolean check(TreeNode s, TreeNode t){
  if(null == s && null == t) return true;
  if(null == s || null == t) return false;
  if(s.val == t.val){
    return check(s.left,t.left) && check(s.right,t.right);
  }else{
    return false;
  }
}
public boolean isSubtree(TreeNode s, TreeNode t) {
  // 从s里找t
  // 遍历s
  if(null == t || null == s) return false;
  if(s.val == t.val){
    if(check(s,t))return true;
  }
  return isSubtree(s.left,t) || isSubtree(s.right,t);
}

Construct Binary Tree from Preorder and Inorder Traversal

用前序+中序恢复二叉树

Construct Binary Tree from Inorder and Postorder Traversal，106

用中序+后序恢复二叉树

思路：

  • 中序遍历：左 + 根 + 右
  • 后序遍历：左 + 右 + 跟

因此后序遍历可以直接确定根节点；然后去中序里面找根节点。找到根节点后，就可以确定左右子树的大小。那么就可以继续递归了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public TreeNode buildTree(int[] inorder, int[] postorder) {
    if(inorder.length == 0) return null;
    return helper(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
}
private TreeNode helper(int[] inorder, int inLow, int inHigh, int[] postorder, int postLow, int postHigh){
    // 中序遍历：左 + 根 + 右
    // 后序遍历：左 + 右 + 跟
    if(inLow > inHigh || postLow > postHigh) return null;
    TreeNode root = new TreeNode(postorder[postHigh]);
    if(postLow == postHigh) return root;
    //System.out.println(inLow + "\t" + inHigh + "\t" + postLow + "\t" + postHigh);
    // 从中序遍历中寻找根节点的idx
    int rootIdx = inLow;
    for(rootIdx = inLow; rootIdx <= inHigh; ++rootIdx){
        // 这里其实可以用hashmap优化
        if(inorder[rootIdx] == postorder[postHigh])break;
    }
    int leftNum = rootIdx - inLow;
    root.left = helper(inorder, inLow, rootIdx - 1, postorder, postLow, postLow + leftNum - 1);
    root.right = helper(inorder, rootIdx + 1, inHigh, postorder, postLow + leftNum, postHigh - 1);
    return root;
}

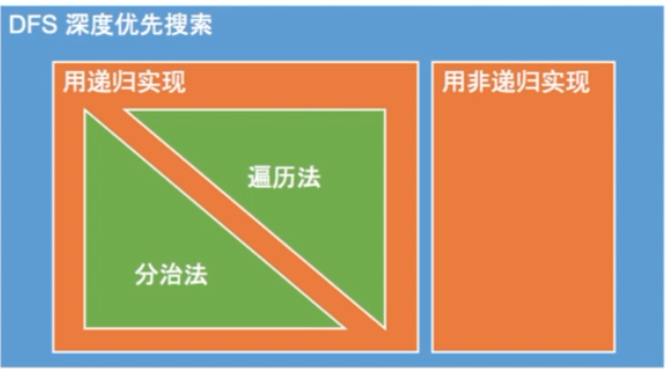
DFS

DFS有两种实现方式：

  • 非递归
  • 递归 -- 有两种选择：
    • 分治
    • 遍历

碰到二叉树问题，就想想整棵树上在该问题上的结果是什么，左右儿子在该问题上的结果之间的联系是什么

Symmetric Tree，101

验证一个二叉树是否是镜像的

思路就是分成两路探索，一路左边，一路右边。

1
2
3
4
5
6
7
8
9
10
11
private boolean helper(TreeNode leftBranch, TreeNode rightBranch){
    if(leftBranch == null && rightBranch == null) return true;
    if(leftBranch == null || rightBranch == null) return false;
    return (leftBranch.val == rightBranch.val) &&
            helper(leftBranch.left, rightBranch.right)&&
            helper(leftBranch.right, rightBranch.left);
}
public boolean isSymmetric(TreeNode root) {
    if(root == null) return true;
    return helper(root.left, root.right);
}

Path Sum

给一个二叉树和一个target。求二叉树的某个路径和是否完全等于target。

基础题：Binary Tree Paths，可以考虑先做这个基础题，然后在做这些

思路：递归就好

1
2
3
4
5
6
7
8
9
10
private boolean helper(TreeNode node, int sum, int target){
       if(node.left == null && node.right == null) return sum == target;
       return (node.left != null && helper(node.left, sum + node.left.val, target) ||
               node.right != null && helper(node.right, sum + node.right.val, target));

   }
   public boolean hasPathSum(TreeNode root, int target) {
       if(root == null) return false;
       return helper( root, root.val, target);
   }

Path Sum II

给一个二叉树和一个target。求二叉树的路径和完全等于target的所有路径

还是递归哇

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
List<List<Integer>> result = new LinkedList<>();
  private void helper(TreeNode node, int sum, List<Integer> list, int target){
      if(node.left == null && node.right == null){
          if(sum == target){result.add(new ArrayList<>(list));}
          return;
      }
      if(node.left != null){
          list.add(node.left.val);
          helper(node.left, sum + node.left.val, list, target);
          list.remove(list.size() - 1);
      }
      if(node.right != null){
          list.add(node.right.val);
          helper(node.right, sum + node.right.val, list, target);
          list.remove(list.size() - 1);
      }

  }
  public List<List<Integer>> pathSum(TreeNode root, int target) {
      if(root != null){
          List<Integer> lists = new LinkedList<Integer>();
          lists.add(root.val);
          helper(root, root.val,lists , target);
      }
      return result;
  }

Path Sum III

给一个二叉树和一个target。求二叉树某点到其的某个子节点的和等于target的个数。

思路：其实这道题类似于单条路径上的这道题：560. Subarray Sum Equals K

在dfs时，存储当前节点i路径下的所有父节点j到root的和。那么sum[i,j] = sum[i] - sum[j]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int counter = 0;
private void helper(TreeNode node, int[] sums, int level, int target){
    // 先检查本节点是否存在于上面节点的和==target的情况
    if(sums[level] == target) ++counter;
    for(int i = 0; i < level; ++i){
        // System.out.println(i + "\t" + (sums[level] - sums[i]));
        if(sums[level] - sums[i] == target) ++counter;
    }
    // sum存储从根节点到本节点，每个节点的到root的和
    if(node.left != null){
        sums[level + 1] = sums[level] + node.left.val;
        helper(node.left, sums, level + 1, target);
        sums[level + 1] = 0;
    }
    if(node.right != null){
        sums[level + 1] = sums[level] + node.right.val;
        helper(node.right, sums, level + 1, target);
        sums[level + 1] = 0;
    }
}
public int pathSum(TreeNode root, int target) {
    if(root == null) return 0;
    int[] sums = new int[1001];
    sums[0] = root.val;
    helper(root, sums, 0, target );
    return counter;
}

优化：所有和还可以用hash表存储！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int counter = 0;
  private void helper(TreeNode node, HashMap<Integer, Integer> sums, int lastSum, int target){
      // 检查与根节点
      int thisSum = lastSum + node.val;
      if(thisSum == target) ++counter;
      //检查与其它节点
      if(sums.containsKey(thisSum - target)) {
          counter += sums.get(thisSum - target);
      }
      //将本节点加入
      if(sums.containsKey(thisSum)){
          sums.replace(thisSum, sums.get(thisSum) + 1);
      }
      else sums.put(thisSum, 1);
      if(node.left != null){
          helper(node.left, sums,thisSum, target);
      }
      if(node.right != null){
          helper(node.right, sums, thisSum, target);
      }
      //将本节点挪出
      if(sums.get(thisSum) > 1) sums.replace(thisSum, sums.get(thisSum) - 1);
      else sums.remove(thisSum);
  }
  public int pathSum(TreeNode root, int target) {
      if(root == null) return 0;
      HashMap<Integer, Integer> sums = new HashMap<>();
      helper(root, sums, 0, target );
      return counter;
  }

Trim a Binary Search Tree

修剪二叉树，使得值在[L,R] 之间。修剪时，优先保留左子树。

1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode trimBST(TreeNode root, int L, int R) {
        if(root == null)return root;
        if(root.val >= L && root.val <= R){
            root.left = trimBST(root.left, L, R);
            root.right = trimBST(root.right, L, R);
        }else{
            TreeNode left = trimBST(root.left, L, R);
            if(null != left) root = left;
            else root = trimBST(root.right, L, R);
        }
        return root;
    }

BFS相关例题

BFS最重要的两个数据结构：

  • 队列
  • 哈希表

层序遍历

例题1，Binary Tree Level Order Traversal，102

队列！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
if(null == root){
  return result;
}
// interface
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
  int size =queue.size();
  ArrayList<Integer> currentLevel = new ArrayList<>();
  for(int i = 0; i < size; i++){
    TreeNode head = queue.poll();
    currentLevel.add(head.val);
    if(head.left != null){
      queue.offer(head.left);
    }
    if(head.right != null){
      queue.offer(head.right);
    }
  }
  result.add(currentLevel);
}
return result;

Binary Tree Level Order Traversal II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public List<List<Integer>> levelOrderBottom(TreeNode root) {
        LinkedList<List<Integer>> result = new LinkedList<>(); 
        // LinkedList是List接口的实现，所以可以直接使用
        if(null == root) return result;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            int size = queue.size();
            List<Integer> curResult = new LinkedList<>();
            while (size > 0){
                TreeNode cur = queue.poll();
                curResult.add(cur.val);
                if(null != cur.left){
                    queue.offer(cur.left);
                }
                if(null != cur.right){
                    queue.offer(cur.right);
                }
                --size;
            }
            result.addFirst(curResult); // 注意这个神奇的东西
        }
        return result;
    }

Binary Tree Zigzag Level Order Traversal，103

输出二叉树的层序遍历，且需要隔层倒序。

思路：用一个linkedList就好啦

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
  List<List<Integer>> result = new LinkedList<>();
  if(null == root) return result;
  Queue<TreeNode> queue = new LinkedList<>();
  queue.offer(root);
  boolean fromHead = false;
  while (!queue.isEmpty()){
    int size =queue.size();
    LinkedList<Integer> oneResult = new LinkedList<>();
    while (size > 0){
      TreeNode now = queue.poll();
      if(fromHead){
        oneResult.addFirst(now.val);
      }else {
        oneResult.addLast(now.val);
      }
      if(null != now.left) queue.offer(now.left);
      if(null != now.right)queue.offer(now.right);
      --size;
    }
    fromHead = !fromHead;
    result.add(oneResult);
  }
  return result;
}

思路2：用两个栈，单数层先left后right，双数层先right后left

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public ArrayList<ArrayList<Integer>> zigzagLevelOrder(TreeNode root) {
    // write your code here
    ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
    if (root == null) {
        return result;
    }
    // currLevel表示当前在处理的那一层的结点
    // nextLevel表示下一层要处理的结点
    Stack<TreeNode> currLevel = new Stack<TreeNode>();
    Stack<TreeNode> nextLevel = new Stack<TreeNode>();
    Stack<TreeNode> tmp;

    currLevel.push(root);
    boolean normalOrder = true;

    while (!currLevel.isEmpty()) {
        ArrayList<Integer> currLevelResult = new ArrayList<Integer>();

        while (!currLevel.isEmpty()) {
            TreeNode node = currLevel.pop();
            currLevelResult.add(node.val);

            if (normalOrder) {
                if (node.left != null) {
                    nextLevel.push(node.left);
                }
                if (node.right != null) {
                    nextLevel.push(node.right);
                }
            } else {
                if (node.right != null) {
                    nextLevel.push(node.right);
                } 
                if (node.left != null) {
                    nextLevel.push(node.left);
                }
            }
        }
        result.add(currLevelResult);
        // 交换currLevel和nextLevel，currLevel代表将要处理的那一层结点
        tmp = currLevel;
        currLevel = nextLevel;
        nextLevel = tmp;

        normalOrder = !normalOrder;
    }

}

Binary Tree Right Side View，199

给一个二叉树。从最右边看去，能看到的数字都是几？

思路：层序遍历，输出每层的最后一个元素！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public List<Integer> rightSideView(TreeNode root) {
    List<Integer> result = new LinkedList<>();
    if(root == null) return result;
    // 层序遍历的最后一个
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()){
        int size = queue.size();
        TreeNode temp = null;
        while (size > 0){
            temp = queue.poll();
            if(temp.left != null) queue.add(temp.left);
            if(temp.right != null) queue.add(temp.right);
            --size;
        }
        result.add(temp.val);
    }
    return result;
}

Populating Next Right Pointers in Each Node I 和II

给一个二叉树，每个节点应该有一个兄弟节点，但输入前兄弟节点还是空的。完成一个函数实现它。

思路一：层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void connect(TreeLinkNode root) {
        if(root == null) return;
        Queue<TreeLinkNode> level = new LinkedList<>();
        level.add(root);
        while (!level.isEmpty()){
            int size = level.size();
            TreeLinkNode last = null;
            while (size-- > 0){
                TreeLinkNode curr = level.poll();
                if(curr.left != null)level.add(curr.left);
                if(curr.right != null)level.add(curr.right);
                if(last == null){
                    last = curr;
                    continue;
                }else {
                    last.next = curr;
                    last = curr;
                }
            }
        }
    }

思路2，骚操作 —— 只适合I，不适合II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 满二叉树！
   node       next
   /  \       / \
left right left right

node.right.next = node.next.left !!!!!

public void connect(TreeLinkNode root) {
        while (null != root){
            TreeLinkNode cur = root;
            while (cur != null){
                if(cur.left != null)cur.left.next = cur.right;
                if(cur.right != null && cur.next != null) cur.right.next = cur.next.left;
                cur = cur.next;
            }
            root = root.left;
        }
    }

Minimum Depth of Binary Tree，111

返回二叉树叶子结点的最小的层数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int minDepth(TreeNode root) {
  if(null == root) return 0;
  Queue<TreeNode> queue = new LinkedList<>();
  int level = 1;
  queue.offer(root);
  while (!queue.isEmpty()){
    int size = queue.size();
    while (size > 0){
      TreeNode now = queue.poll();
      if(null == now.right && null == now.left) return level;
      if(null != now.left) {queue.offer(now.left);}
      if(null != now.right) {queue.offer(now.right);}
      --size;
    }
    ++level;
  }
  return level;
}

Find Largest Value in Each Tree Row

输出二叉树每行的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public List<Integer> largestValues(TreeNode root) {
    List<Integer> result = new LinkedList<>();
    if(root == null) return result;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()){
        int size = queue.size();
        int max = Integer.MIN_VALUE;
        while (size > 0){
            root = queue.poll();
            max = Math.max(max, root.val);
            if(root.left != null) queue.add(root.left);
            if(root.right != null) queue.add(root.right);
            --size;
        }
        result.add(max);
    }
    return result;
}

01 Matrix

给一个矩阵。将这个矩阵变为：每个元素的值=它与最近的0的距离

这个操作还是第一次遇到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int[][] updateMatrix(int[][] matrix) {
        if(matrix.length == 0  || matrix[0].length == 0)return matrix;
        int m = matrix.length;
        int n = matrix[0].length;
        Queue<int[]> queue = new LinkedList<>();
        // 队列维护当前已确定的方格
        for(int i = 0; i < m; ++i){
            for(int j = 0; j < n; ++j){
                if(matrix[i][j] == 0) queue.add(new int[]{i,j});
                else matrix[i][j] = Integer.MAX_VALUE;
            }
        }
        int[] dx = {1,0,-1,0};
        int[] dy = {0,1,0,-1};
        while (!queue.isEmpty()){
            int[] pair = queue.poll();
            for(int k = 0; k < 4; ++k){
                if(matrix[pair[0]+dx[k]][pair[1]+dy[k]] < matrix[pair[0]][pair[1]] + 1) continue;
                matrix[pair[0]+dx[k]][pair[1]+dy[k]] = matrix[pair[0]][pair[1]] + 1;
                queue.add(new int[]{pair[0]+dx[k],pair[1]+dy[k] });
            }
        }
        return matrix;
    }

Word Ladder

输入的是：一个单词和一个字典，单词每次只允许改变一个字母变成字典中的某个单词，如此循环，判断是否能变成目标单词，如果能的话返回变换次数，否则返回0。

  1. 将每个单词看成图的一个节点。
  2. 当单词s1改变一个字符可以变成存在于字典的单词s2时，则s1与s2之间有连接。
  3. 给定s1和s2，问题I转化成了求在图中从s1->s2的最短路径长度。而问题II转化为了求所有s1->s2的最短路径。

无论是求最短路径长度还是求所有最短路径，都是用BFS。在BFS中有三个关键步骤需要实现:

  1. 如何找到与当前节点相邻的所有节点。 这里可以有两个策略：
  1. 遍历整个字典，将其中每个单词与当前单词比较，判断是否只差一个字符。复杂度为：n*w，n为字典中的单词数量，w为单词长度。
  2. 遍历当前单词的每个字符x，将其改变成a~z中除x外的任意一个，形成一个新的单词，在字典中判断是否存在。复杂度为：26*w，w为单词长度。 这里可以和面试官讨论两种策略的取舍。对于通常的英语单词来说，长度大多小于100，而字典中的单词数则往往是成千上万，所以策略2相对较优。
  1. 如何标记一个节点已经被访问过，以避免重复访问。 可以将访问过的单词从字典中删除。
  2. 一旦BFS找到目标单词，如何backtracking找回路径？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
这道题写了有五六个小时。气死了。


private int hammin(String a, String b){
        int dist = 0;
        for(int i = 0; i < a.length(); ++i){
            if(a.charAt(i) == b.charAt(i)) continue;
            ++dist;
            if(dist > 2) break;
        }
        return dist;
    }
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        if(beginWord.equals(endWord)) return 0;
        boolean[] visited = new boolean[wordList.size()];
        // 层序遍历
        Queue<String> queue = new LinkedList<>();
        queue.add(beginWord);
        int level = 1;
        while (!queue.isEmpty()){
            ++level;
            int size = queue.size();
            while (size-- > 0){
                String currKey = queue.poll();
                // 将所有汉明距离为1的字符加入
                int i = 0;
                for(String s : wordList){
                    if(!visited[i] && hammin(currKey, s) == 1){
                        visited[i] = true;
                        queue.add(s);
                        if(s.equals(endWord)) return level;
                    }
                    ++i;
                }
            }
        }
        return 0;
    }

Minimum Height Trees

给一个无向无环图，求一个节点，使得它到任何点的距离最短。

非常巧妙的思路。从叶子结点开始BFS，每次删掉一层的叶子结点。最后剩的那一层就是结果！

一开始我只想到了半截，没有想到用队列，而是想到用优先队列。也没想通最后一层就是结果。难受。最后参考了他的代码 才想通了这些。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Node{
    int idx;
    List<Integer> neibors;
    int degree = 0;
    Node(int idx){
        this.idx = idx;
        neibors = new LinkedList<>();
    }
}

public List<Integer> findMinHeightTrees(int n, int[][] edges) {
    // 寻找根节点

    Node[] nodes = new Node[n];
    for(int i = 0; i < n; ++i){
        nodes[i] = new Node(i);
    }
    for(int[] edge : edges){
        nodes[edge[0]].neibors.add(edge[1]);
        nodes[edge[1]].neibors.add(edge[0]);
        ++nodes[edge[0]].degree;
        ++nodes[edge[1]].degree;
    }
    // 根节点： acCounter == 1 的节点
    Queue<Integer> queue = new LinkedList<>(); // 存放根节点，这一点一开始没有想到
    for(int i = 0; i < n; ++i){
        if(nodes[i].degree == 1) queue.add(i);
    }
    List<Integer> result = new ArrayList<>();
    while (!queue.isEmpty()){
        result = new ArrayList<>();// 这一步非常巧妙，因为每次BFS的叶子结点的对外层数都相等！
        // BFS删除所有的根节点
        int size = queue.size();
        while (size > 0) {
            --size;
            result.add(queue.peek());
            Node root = nodes[queue.poll()];
            // 删除这个根节点的边
            for (int neibor : root.neibors) {
                --nodes[neibor].degree;
                --root.degree;
                if (nodes[neibor].degree == 1) {
                    queue.add(neibor);
                }
            }
        }
    }
    return result;
}

分治相关例题

例题1，Maximum Depth of Binary Tree

求二叉树的最大深度

方法一，遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

private int max = 0;

//从root出发,root当前深度是1
helper(root,1);

private void helper(TreeNode root, int depth){
  //走过头了
  if( root == null ){
    return;
  }
  max = Math.max(max,depth);
  helper(root.left, depth + 1 );
  helper(root.right, depth + 1 )
}

方法2，分治

没有全局变量

1
2
3
4
5
6
7
8
9
public int maxDepth(TreeNode root){
  if( root == null ){
    return 0;
  }
  int leftDepth = maxDepth(root.left);
  int rightDepth = maxDepth(root.right);
  
  return Math.max(leftDepth,rightDepth) + 1;
}

例题2，Balanced Binary Tree

判断一个树是不是平衡二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//当一个结果有多个参数决定时，定义一个class
class ResultType{
  public boolean isBalanced;
  public int maxDepth;
  public ResultType(boolean isBalanced, int maxDepth){
    this.isBalanced = isBalanced;
    this.maxDepth = maxDepth;
  }
}

// 主函数
public boolean isBalanced(TreeNode root){
  return helper(root).isBalanced;
}
// 分治
private ResultType helper(TreeNode root){
  if(null == root){
    return new ResultType(true,0);
  }
  ResultType left = helper(root.left);
  ResultType right = helper(root.right);
  
  // 子树不平衡
  if(!left.isBalanced || !right.isBalanced){
    return new ResultType(false,-1);
  }
  // root不平衡
  if(Math.abs(left.maxDepth - right.maxDepth) > 1){
    return new ResultType(false,-1);
  }
  return new ResultType(true,Math.max(left.maxDepth , right.maxDepth) + 1);
}

另一种解法：

1
2
3
4
5
6
7
8
9
10
11
12
public int helper(TreeNode root){
  if(null == root) return 0;
  int leftDepth = helper(root.left);
  if(leftDepth == -1) return -1;
  int rightDepth = helper(root.right);
  if(rightDepth == -1) return -1;
  if(Math.abs(leftDepth-rightDepth)>1)return -1;
  return Math.max(leftDepth,rightDepth) + 1;
}
public boolean isBalanced(TreeNode root) {
  return helper(root)!=-1;
}

例题3，Lowest Common Ancestor，236

求一颗二叉树中两个点a,b的最近公共祖先

在root为根的二叉树中，从上到下寻找A,B的LCA:

  • 如果找到了就返回这个LCA
  • 如果只碰到A，就返回A
  • 如果只碰到B，就返回B
  • 如果都没有，就返回null
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode nodel1, TreeNode node2){
  if(root == null || root == node1 || root == node2){
    // 很有趣的点：如果root是node1，且root包含node2，那么此时别的node就不可能返回非null了。那么此时root肯定是了。
    return root;
  }
  // 分解问题
  TreeNode left = lowestCommonAncestor(root.left, node1, node2);
  TreeNode right = lowestCommonAncestor(root.right, node1, node2);
  
  // 合并问题
  if(left != null && right != null){ // left中含有n1或n2,right也含有
    return root;
  }
  if(right != null){ // right中含有n1或n2,left不含
    return right;
  }
  if(left != null){ // left中含有n1或n2,right不含
    return left;
  }
  return null;
}

另一种思路，统计本节点的子节点中有几个命中节点 如果等于两个，则本节点是公共祖先！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
TreeNode result;
public int helper(TreeNode root, TreeNode p,TreeNode q){
  int counter = 0;
  if( null == root || null != result) return counter;
  if( root == p ) {
    counter += 1;
  }else if( root == q ) {
    counter += 1;
  }
  if( counter == 2 ){
    if(null == result)result = root;
    return counter;
  }
  counter += helper(root.right,p,q);
  if( counter == 2 ){
    if(null == result)result = root;
    return counter;
  }
  counter += helper(root.left,p,q);
  if( counter == 2 ){
    if(null == result)result = root;
    return counter;
  }

  return counter;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

  int counter = helper(root,p,q);
  return result;
}

例题4，Lowest Common Ancestor II

1
2
3
4
5
在root为跟的二叉树中找n1,n2的LCA
如果找到了就返回
如果只碰到了n1,就返回n1
如果只碰到了n2,就返回n2
如果都没有，就返回Null

例题5，Binary Tree Maximum Path Sum II

给一个二叉树，找到从root的最大路径和。路径可以在任何地方被结束掉。

1
2
3
4
5
6
7
8
9
   1
  / \
 2   3
      \
       -1

return 4

思路：某个点的最大长度 = Math.max(0,sum)

例题6，Binary Tree Maximum Path Sum，124

给一个二叉树，找到从any node 到 any node最大路径和。路径可以在任何地方被结束掉。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
  -1
  / \
 2   3
      \
       -1

return 3

思路：两个分治

要求整个二叉树的最长路径，先求左子树的最长路径，再求右子树的最长路径。

整棵树的最长路径（以上图为例）：
1. 有可能全在左边（只有2）
2. 有可能全在右边（只有3）
3. 可能跨过root节点（有-1、2、3）

class ResultType{
 int root2This, any2This;
 ResultType(int root2This, int any2This){
   this.root2This = root2This; 
   this.any2This = any2This;
 }
}

private ResultType helper(TreeNode root){
  // illegal
  if(null == root){
    return new ResultType(Integer.MIN_VALUE,Integer.MIN_VALUE);
  }
  // 分解问题
  ResultType left = helper(root.left);
  ResultType right = helper(root.right);
  
  // 合并问题
  // 为了方便之后的第3步计算（为了解决any2this，一定要算出root2this）
  int root2This = Math.max(0,Math.max(left.root2This, right.root2This)) + root.val;
  
  // 1、2. root到这个节点的最大sum
  // 全在左边或者全在右边（可以不包含root）
  int any2This = Math.max(left.any2This, right.any2This);
  // 3. any到这个节点的最大sum
  // 跨过了root点（一定是root到left或right的路径）
  any2This = Math.max(any2This,
                     Math.max(0, left.root2This)
                     + Math.max(0, right.root2This)
                     + root.val);
                     
  return new Result(root2This, any2This);
}

代码：
// int[0] - > any 2 any
// int[1] --> end 2 this
public int[] helper(TreeNode node) {
        if(null == node) return new int[]{-9999999,-9999999};
        int[] left = helper(node.left);
        int[] right = helper(node.right);
        // 从本节点向下的某个节点截止
        int down2This = Math.max(
                Math.max(left[1] + node.val,
                        right[1] + node.val),
                node.val
        );
        // 跨越node节点
        int twoside = left[1] + node.val + right[1];
        // 全在左子树或全在右子树
        int oneside  = Math.max(left[0],right[0]);
        // 三者求最大
        int any2This = Math.max(down2This,Math.max(oneside,twoside));
        return new int[]{any2This,down2This};
    }
    public int maxPathSum(TreeNode root) {
     return helper(root)[0];
    }

还有一种骚操作，只记录【本节点】到【下方节点】的最大和！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int max = Integer.MIN_VALUE; // 全局最大
public int maxPathSum(TreeNode root) {
  if(root == null) return 0;
  traverse(root);
  return max;
}

private int traverse(TreeNode root) {
  if(root == null) return 0;
  int left = traverse(root.left);
  int right = traverse(root.right);
  max = Math.max(max, Math.max(left, 0) + Math.max(right, 0) + root.val);
  return Math.max(0, Math.max(left, right)) + root.val;
}

Invert Binary Tree，226

将二叉树镜像反转（左右替换）

1
2
3
4
5
6
7
8
public TreeNode invertTree(TreeNode root) {
     if(root == null) return null;
     TreeNode left = invertTree(root.left);
     TreeNode right = invertTree(root.right);
     root.left = right;
     root.right = left;
     return root;
 }

二叉搜索树

BST定义

定义

  • 左子树比根节点小
  • 右子树比根节点大
    • 如果有重复，可以全部放在左/右

效果

  • 中序遍历是升序序列

性质

  • 如果一颗二叉树中序不是升序，则一定不是BST
  • 如果一颗二叉树中序是升序，则不一定是BST

删除

本节主要参考自：【算法导论】二叉搜索树的插入和删除

从一个二叉搜索树中删除一个结点，会有三种情况：

  • 如果z没有孩子节点，就直接删除，并修改它的父节点，用null作为它的孩子；

  • 如果z只有一个孩子，就将这个孩子提升到树中z的位置上，并修改z的父节点，用z的孩子来替换z；

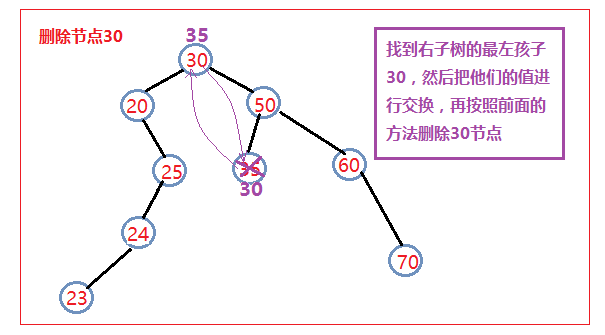
  • 如果z有两个孩子，那么可以寻找节点的后继（中序遍历时的下一个结点）。删除方法如下：

    • 找到该节点的右子树中的最左孩子（也就是右子树中序遍历的第一个节点）
    • 把它的值和要删除的节点的值进行交换
    • 然后删除这个节点（其实就是用这个节点的右子树替换这个节点，因为这个节点此时已经肯定没有左子树了）

代码见后面的题- Delete Node in a BST

Validate Binary Search Tree，98

验证一个二叉树是不是搜索二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
BST有一个性质——如果一个二叉树的中序遍历是严格递增的，则这个二叉树一定是BST.

public boolean isValidBST(TreeNode root) {
  Stack<TreeNode> stack = new Stack<>();
  long last = Long.MIN_VALUE;
  while (!stack.isEmpty() || null != root){
    while (null != root){
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    if(last < root.val){
      last = root.val;
    }else {
      return false;
    }
    root = root.right;
  }
  return true;
}

Binary search Tree Iterator，173

中序遍历。要一个给一个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

public class BSTIterator {
    Stack<TreeNode> stack;
    TreeNode root;
    public BSTIterator(TreeNode root) {
        this.root = root;
        stack= new Stack<>();
    }

    /** @return whether we have a next smallest number */
    public boolean hasNext() {
        return!stack.isEmpty() || null != root;
    }

    /** @return the next smallest number */
    public int next() {
        while (null != root){
            stack.push(root);
            root = root.left;
        }
        root = stack.pop();
        int result =root.val ;
        root = root.right;
        return result;
    }
}

/**
 * Your BSTIterator will be called like this:
 * BSTIterator i = new BSTIterator(root);
 * while (i.hasNext()) v[f()] = i.next();
 */

Convert Sorted Array to Binary Search Tree

将有序数组转化为平衡二叉树

思路：平衡二叉树的root一定是有序数组的中点！

1
2
3
4
5
6
7
8
9
10
11
12
13
public TreeNode helper(int[] nums, int start, int end){
       if(end < start) return null;

       int mid = start + (end - start)/2;
       TreeNode root = new TreeNode(nums[mid]);
       root.left = helper(nums,start,mid - 1);
       root.right = helper(nums,mid + 1 ,end);
       return root;
   }
   public TreeNode sortedArrayToBST(int[] nums) {
       if(nums.length == 0) return null;
       return helper(nums,0,nums.length-1);
   }

Convert Sorted List to Binary Search Tree

将有序链表转化为平衡二叉树

这道题思路实在是太骚气了

我们换一个思路可能就会简单很多，即如果是将一个排序二叉树转换成链表，无非是一个中序遍历。

那么，这里讲链表转换成二叉树也是一样的思路，即一个中序遍历，其具体思路如下。

按照中序遍历的思路，应该先生成左子树，然后是根节点，最后的右子树。以这样的顺序，每次新创建的节点都对应链表的顺序遍历中当前位置的节点。

很明显这是一个递归的结构。那么剩下的问题就是如何确定递归的终止条件。

因为在转换的过程中，需要计算各子链表的长度，那么这里就可以由此来终止递归，即当长度等于0时终止。下面我们来看代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
private int getLength(ListNode head){
       int length = 0;
       while (null != head){
           head = head.next;
           ++length;
       }
       return length;
   }
   ListNode curr;
   public TreeNode sortedListToBST(ListNode head) {
       int size = getLength(head);
       curr = head;
       return helper(size);
   }
   public TreeNode helper(int size){
       if(size == 0) return null;
       TreeNode left = helper(size / 2);
       TreeNode root = new TreeNode(curr.val);
       curr = curr.next;
       root.left = left;
       root.right = helper(size - size / 2 - 1);
       return  root;
   }

Delete Node in a BST

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public TreeNode deleteNode(TreeNode root, int key) {
        if(null == root){
            return null;
        }
        TreeNode dummy = new TreeNode(0);
        if(root.val < 0){dummy.left = root;
        }else{dummy.right = root;}
        TreeNode parent = dummy;
        TreeNode child = root;
        while (null != child){
            if(child.val == key){
                break;
            }else if(child.val < key){
                parent = child;
                child = child.right;
            }else {
                parent = child;
                child = child.left;
            }
        }
        if(null == child){
            return root;
        }
        if(null == child.left){
            if(child.val < parent.val){
                parent.left = child.right;
            }else {
                parent.right = child.right;
            }
        }else if(null == child.right){
            if(child.val < parent.val){
                parent.left = child.left;
            }else {
                parent.right = child.left;
            }
        }else{ // 都不为空
            // 找到该节点的右子树中的最左孩子
            TreeNode afterParent = child;
            TreeNode after = child.right;
            while (null != after.left){
                afterParent = after;
                after = after.left;
            }
            // 把它的值与删除的节点的值进行交换
            int temp = after.val;
            after.val = child.val;
            child.val = temp;
            // 删除这个节点
            if(temp < afterParent.val){
                afterParent.left = after.right;
            }else{
                afterParent.right = after.right;
            }
        }
        if(null != dummy.left){
            return dummy.left;
        }else{
            return dummy.right;
        }
    }

还有一种递归写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public TreeNode deleteNode(TreeNode root, int key) {
       if (root == null) return null;
       
       if (root.val > key) {
           root.left = deleteNode(root.left, key);
       } else if (root.val < key) {
           root.right = deleteNode(root.right, key);
       } else {
           if (root.left == null) return root.right;
           if (root.right == null) return root.left;
           
           TreeNode rightSmallest = root.right;
           while (rightSmallest.left != null) rightSmallest = rightSmallest.left;
           rightSmallest.left = root.left;
           return root.right;
       }
       return root;
   }

Find Mode in Binary Search Tree

给一个有重的BST。其中左子树小于等于本身，右子树大于本身。统计最多次数出现的数字。

思路：中序遍历计数即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int maxCount;
    List<Integer> set;

    public int[] findMode(TreeNode root) {
        maxCount = 0;
        set = new LinkedList<>();
        Stack<TreeNode> stack = new Stack<>();
        int preVal = Integer.MAX_VALUE;
        int preCount = 0;
        while (!stack.isEmpty() || null != root){
            while (null != root){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if(root.val == preVal){
                ++preCount;
            }else {
                preVal = root.val;
                preCount = 1;
            }
            if(preCount > maxCount){
                set.clear();
                set.add(preVal);
                maxCount = preCount;
            }else if(preCount == maxCount){
                set.add(preVal);
            }
            root = root.right;
        }

        int[] res = new int[set.size()];
        int i = 0;
        for(int e : set){
            res[i] = e;
            ++i;
        }
        return res;
    }

Serialize and Deserialize BST

实现BST的序列化和反序列化。

我的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if (root == null) return "";
        StringBuilder sb = new StringBuilder();
        sb.append(root.val);
        sb.append(",");
        if(root.left != null) sb.append(serialize(root.left));
        if(root.right != null) sb.append(serialize(root.right));
        return sb.toString();
    }
    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] str = data.split(",");
        if(str.length == 0) return null;
        if(str[0].length() == 0) return null;
        Stack<TreeNode> stack = new Stack<>();
        TreeNode root = new TreeNode(Integer.valueOf(str[0]));
        stack.push(root);
        for(int i = 1; i < str.length; ++i){
            TreeNode curr = new TreeNode(Integer.valueOf(str[i]));
            // 为当前的curr节点寻找插入位置
            TreeNode out = null;
            // 将所有比curr小的节点全pop出去
            //（除了最后一个pop出去的节点外，
            // 这些比curr小的节点都不可能有左右子树了）
            while (!stack.isEmpty() && curr.val > stack.peek().val){
                out = stack.pop();
            }
            // 如果curr大于最后一个pop出去的节点，那curr一定是最后一个pop出去的右节点
            if(out != null && curr.val > out.val){
                out.right = curr;
            }else{
                // 否则，那它就是栈顶的左节点
                stack.peek().left = curr;
            }
            stack.push(curr);
        }
        return root;
    }

还有很多相关题。

完全二叉树

Count Complete Tree Nodes

求完全二叉树的节点个数。

一开始就暴力数，当然是超时了。

下面是一种参考网上的巧妙的解法。主要是二分 + 位操作 \(2^n = n << 1\)

完全二叉树的一个性质是，如果左子树最左边的深度，等于右子树最右边的深度，说明这个二叉树是满的，即最后一层也是满的，则以该节点为根的树其节点一共有2^h-1个。如果不等于，则是左子树的节点数，加上右子树的节点数，加上自身这一个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
private int LeftLevel(TreeNode node){
        if(node == null) return 0;
        return 1 + LeftLevel(node.left);
    }
    private int rightLevel(TreeNode node){
        if(node == null) return 0;
        return 1 + rightLevel(node.right);
    }
    private int helper(TreeNode node){
        if(node == null) return 0;
        int leftLevel = LeftLevel(node.left) + 1;
        int rightLevel = rightLevel(node.right) + 1;
        if(leftLevel == rightLevel){ // 满二叉树节点个数 = 2^n - 1
            //System.out.println(node.val + "\t" + leftLevel + "\t" + ((leftLevel << 1) - 1));
            return  (1 << leftLevel) - 1;
        }
        int nodeNums = helper(node.left) + helper(node.right) + 1;
        //System.out.println(node.val + "\t" + leftLevel + "\t" + nodeNums);
        return nodeNums;
    }
    public int countNodes(TreeNode root) {
        return helper(root);
    }

在这其中是存在重复计算的。同一个节点的数高度可能被计算多次。下面这种解法巧妙地避开了重复计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public int countNodes(TreeNode root) {
        return countNodes(root, -1, -1);
    }
    
    private int countNodes(TreeNode root, int lheight, int rheight){
        // 如果没有上轮计算好的左子树深度，计算其深度
        if(lheight == -1){
            lheight = 0;
            TreeNode curr = root;
            while(curr != null){
                lheight++;
                curr = curr.left;
            }
        }
        // 如果没有上轮计算好的右子树深度，计算其深度
        if(rheight == -1){
            rheight = 0;
            TreeNode curr = root;
            while(curr != null){
                rheight++;
                curr = curr.right;
            }
        }
        // 如果两个深度一样，返回2^h-1
        if(lheight == rheight) return (1 << lheight) - 1;
        // 否则返回左子树右子树节点和加1
        return 1 + countNodes(root.left, lheight - 1, -1) + countNodes(root.right, -1, rheight - 1);
    }

骚操作

还有一种操作：

用迭代法的思路稍微有点不同，因为不再是递归中那样的分治法，我们迭代只有一条正确的前进方向。所以，我们判断的时左节点的最【左】边的深度，和右节点的最【左】边深度。因为最后一层结束的地方肯定在靠左的那侧，所以我们要找的就是这个结束点。如果两个深度相同，说明左子树和右子树都是满，结束点在右侧，如果右子树算出的最左深度要小一点，说明结束点在左边，右边已经是残缺的了。根据这个大小关系，我们可以确定每一层的走向，最后找到结束点。另外，还要累加每一层的节点数，最后如果找到结束点，如果结束点是左节点，就多加1个，如果结束点是右节点，就多加2个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public int countNodes(TreeNode root) {
        int count = 0;
        int h = minHeight(root);
        while (root != null) {
            int leftH = h - 1;
            int rightH = minHeight(root.right);
            if (rightH == leftH) { // 是满二叉树
                count += 1 + getCount(leftH);
                root = root.right;
                h = rightH;
            } else { //肯定是左边残缺
                count += 1 + getCount(rightH);
                root = root.left;
                h = leftH;
            }
        }
        return count;
    }
    
    private int minHeight(TreeNode root) {
        int h = 0;
        while (root != null) {
            root = root.left;
            h++;
        }
        return h;
    }
    
    private int getCount(int h) {
        return (1 << h) - 1;
    }

参考文献

  1. 刷题】二叉树非递归遍历
  2. 二叉树前序，中序，后序遍历迭代实现详解
  3. 【算法导论】二叉搜索树的插入和删除