甲乙小朋友的房子

甲乙小朋友很笨，但甲乙小朋友不会放弃

0%

深度学习实践-1-4-1-构建深层神经网络

发表于 更新于 分类于 ，

本文主要参考自吴恩达Coursera深度学习课程 DeepLearning.ai 编程作业（1-4）

吴恩达Coursera课程 DeepLearning.ai 编程作业系列，本文为《神经网络与深度学习》部分的第四周“深层神经网络”的课程作业。

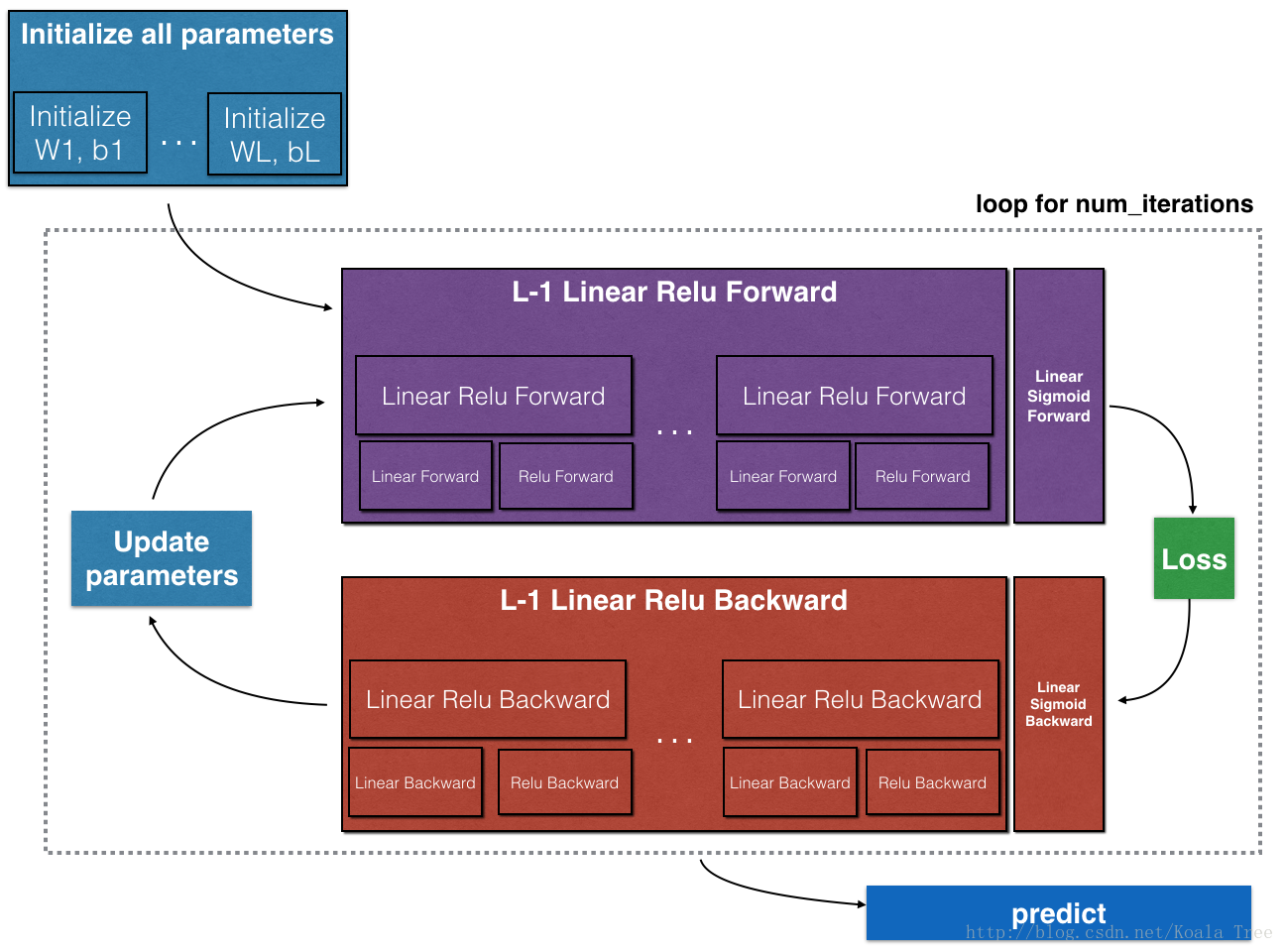
本节的主要内容是：实现L层的神经网络

大纲

首先完成一些helper function。然后再建立两层、多层神经网络：

  • 两层和多层神经网络的初始化
  • 实现前向传播模型
    • 实现某一层的前向传播 - 输出\(Z^{[l]}\)
    • 激活层已给出
    • 将前两步结合
    • 将前向传播迭代L-1次，然后将激活层加到最后，就完成了L层的前向传播
  • 计算误差
  • 实现后向传播模型
    • 实现某一层的后向传播
    • 激活层的后向传播已给出
    • 将前两步结合
    • 将后向传播迭代L-1次，然后将激活层加到最后，完成了L层的后向传播
  • 更新参数

import

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import warnings
warnings.filterwarnings("ignore") 

import numpy as np
import h5py
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

初始化

  • 完成两层模型的初始化
  • 完成多层模型的初始化

两层模型的初始化

  • 模型结构是： LINEAR - RELU - LINEAR - SIGMOID
  • 用随机数初始化w
  • 用0初始化b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 参数初始化

def initialize_parameters(n_x, n_h, n_y):
    """
    参数：
    n_x -- 输入层的大小
    n_h -- 隐藏层的大小
    n_y -- 输出层的大小
    
    Returns:
    parameters -- python dict ：
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape (n_y, 1)
    """
    # 初始化
    W1 = np.random.randn(n_h, n_x)*0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h)*0.01
    b2 = np.zeros((n_y, 1))
    
    # 验证
    assert(W1.shape == (n_h, n_x))
    assert(b1.shape == (n_h, 1))
    assert(W2.shape == (n_y, n_h))
    assert(b2.shape == (n_y, 1))

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters    

parameters = initialize_parameters(3,2,1)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[ 0.01624345 -0.00611756 -0.00528172]
 [-0.01072969  0.00865408 -0.02301539]]
b1 = [[ 0.]
 [ 0.]]
W2 = [[ 0.01744812 -0.00761207]]
b2 = [[ 0.]]

L层模型的初始化

这个比较复杂。我们先来看一个X.shape = (12288,209)的例子:

W.shape b.shape A A.shape
Layer 1 (n[1],12288) (n[1],1) Z[1]=W[1]X+b[1] (n[1],209)
Layer 2 (n[2],n[1]) (n[2],1) Z[2]=W[2]A[1]+b[2] (n[2],209)
⋮ ⋮ ⋮ ⋮ ⋮
Layer L-1 (n[L−1],n[L−2]) (n[L−1],1) Z[L−1]=W[L−1]A[L−2]+b[L−1] (n[L−1],209)
Layer L (n[L],n[L−1]) (n[L],1) Z[L]=W[L]A[L−1]+b[L] (n[L],209)

实现： - 模型结构是 [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID . 也就是说，有L-1层的ReLU激活函数，还有一层sigmoid输出 - w用随机初始化 - b用0初始化 - 将\(n^{[l]}\)存入数组变量layer_dims中，代表第l层的n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def initialize_parameters_deep(layer_dims):
    """
    输入：
    layer_dims: 数组变量，代表每一层的维度
    
    Returns:
    parameters -- python dict , 包含 "W1", "b1", ..., "WL", "bL":
            Wl -- 权重矩阵，W1.shape =  (layer_dims[l], layer_dims[l-1])
            bl -- 偏置向量，b1.shape =  (layer_dims[l], 1)

    """
    
    parameters = {}
    L = len(layer_dims) # 网络的层数
    
    for l in range(1, L):
        # 初始化第l层参数
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
        
        # 验证
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
        
    return parameters

parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[ 0.00319039 -0.0024937   0.01462108 -0.02060141 -0.00322417]
 [-0.00384054  0.01133769 -0.01099891 -0.00172428 -0.00877858]
 [ 0.00042214  0.00582815 -0.01100619  0.01144724  0.00901591]
 [ 0.00502494  0.00900856 -0.00683728 -0.0012289  -0.00935769]]
b1 = [[ 0.]
 [ 0.]
 [ 0.]
 [ 0.]]
W2 = [[-0.00267888  0.00530355 -0.00691661 -0.00396754]
 [-0.00687173 -0.00845206 -0.00671246 -0.00012665]
 [-0.0111731   0.00234416  0.01659802  0.00742044]]
b2 = [[ 0.]
 [ 0.]
 [ 0.]]

前向传播

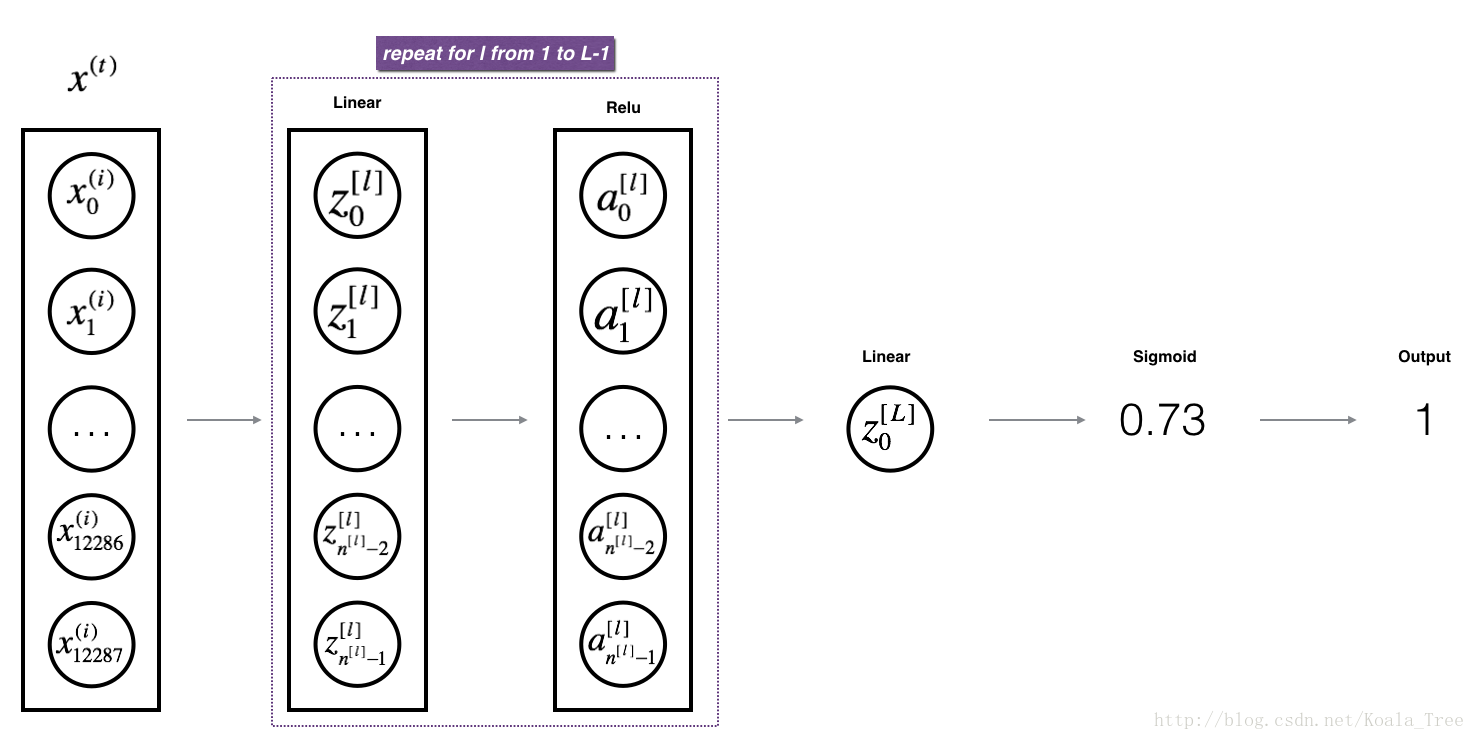
按照如下顺序实现： - LINEAR - LINEAR -> ACTIVATION where ACTIVATION will be either ReLU or Sigmoid. - [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID (whole model)

LINEAR

线性模型如下：

\[Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}\tag{4}\]

where \(A^{[0]} = X\).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def linear_forward(A,W,b):
    """
    实现前向传播的线性部分
    
    输入：
    
    A -- 上一层的输出，也是本层的输入
    W -- 权重矩阵 ， W.shape = (n_(l-1), n_l)
    b -- 偏置向量 ， b.shape = (n_l , 1)
    
    Returns : 
    Z -- 激活函数的输入，也叫"pre-activation parameter"
    cache - dict，包含A,W,b
    """
    
    # 线性部分
    Z = np.dot(W,A) + b
    
    # 验证
    assert(Z.shape == (W.shape[0], A.shape[1]))
    
    # 暂存
    cache = (A, W, b)

    return Z, cache


# 测试函数
def linear_forward_test_case():
    np.random.seed(1)
    """
    X = np.array([[-1.02387576, 1.12397796],
 [-1.62328545, 0.64667545],
 [-1.74314104, -0.59664964]])
    W = np.array([[ 0.74505627, 1.97611078, -1.24412333]])
    b = np.array([[1]])
    """
    A = np.random.randn(3,2)
    W = np.random.randn(1,3)
    b = np.random.randn(1,1)
    
    return A, W, b
# 测试
A, W, b = linear_forward_test_case()

Z, linear_cache = linear_forward(A, W, b)
print("Z = " + str(Z))
Z = [[ 3.26295337 -1.23429987]]

​

LINEAR -> ACTIVATION

本层的公式是：

\(A^{[l]} = g(Z^{[l]}) = g(W^{[l]}A^{[l-1]} +b^{[l]})\)

其中,g()有两种选择：

sigmod ：

\(\sigma(Z) = \sigma(W A + b) = \frac{1}{ 1 + e^{-(W A + b)}}\)

sigmod的实现如下所示

输出: - A - cache = z

ReLU :

\(A = RELU(Z) = max(0, Z)\)

ReLU的实现如下所示 输出： - A - cache = Z

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def sigmoid(Z):
    """
    Implements the sigmoid activation in numpy

    Arguments:
    Z -- numpy array of any shape

    Returns:
    A -- output of sigmoid(z), same shape as Z
    cache -- returns Z as well, useful during backpropagation
    """

    A = 1/(1+np.exp(-Z))
    cache = Z

    return A, cache

def relu(Z):
    """
    Implement the RELU function.

    Arguments:
    Z -- Output of the linear layer, of any shape

    Returns:
    A -- Post-activation parameter, of the same shape as Z
    cache -- a python dictionary containing "A" ; stored for computing the backward pass efficiently
    """

    A = np.maximum(0,Z)

    assert(A.shape == Z.shape)

    cache = Z 
    return A, cache
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
# 实现LINEAR->ACTIVATION层

def linear_activation_forward(A_prev, W, b, activation):
    """
    LINEAR->ACTIVATION的实现
    
    输入：
    A_prev -- 上一层的输出
    W -- 权重矩阵 ， W.shape = (n_l, n_(l-1))
    b -- 偏置向量 ， b.shape = (n_l , 1)
    activation -- 激活的名称，"sigmoid"或"relu"
    
    Returns:
    A -- 激活层输出，也叫post-activation value
    cache  -- python dict, 包含 "linear_cache" 和 "activation_cache"
    """
    
    # 线性输出
    Z, linear_cache = linear_forward(A_prev, W, b)
    
    # 激活
    if activation == "sigmoid":
        A, activation_cache = sigmoid(Z)
        
    elif activation == "relu":
        A, activation_cache = relu(Z)
        
    # 验证
    assert (A.shape == (W.shape[0], A_prev.shape[1]))
    cache = (linear_cache, activation_cache)

    return A, cache
    
    
# 测试
def linear_activation_forward_test_case():
    """
    X = np.array([[-1.02387576, 1.12397796],
 [-1.62328545, 0.64667545],
 [-1.74314104, -0.59664964]])
    W = np.array([[ 0.74505627, 1.97611078, -1.24412333]])
    b = 5
    """
    np.random.seed(2)
    A_prev = np.random.randn(3,2)
    W = np.random.randn(1,3)
    b = np.random.randn(1,1)
    return A_prev, W, b

A_prev, W, b = linear_activation_forward_test_case()

A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "sigmoid")
print("With sigmoid: A = " + str(A))

A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "relu")
print("With ReLU: A = " + str(A))
With sigmoid: A = [[ 0.96890023  0.11013289]]
With ReLU: A = [[ 3.43896131  0.        ]]

L-Model Forward

  • 用RELU，重复之前的linear_activation_forward，L-1次
  • 最后输入SIGMOID 的linear_activation_forward

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
def L_model_forward(X, parameters):
    """
    实现后向传播的[LINEAR->RELU]*(L-1)->LINEAR->SIGMOID步骤
    
    输入：
    
    X -- 数据集
    parameters -- initialize_parameters_deep()的输出，是多层网络初始化后的参数
    
    Returns:
    
    AL -- 最终输出
    caches -- 每层的caches：
            1 ~ L - 1层 的 linear_relu_forward()
            L 层 的 linear_sigmoid_forward()
    """
    
    caches = []
    L = len(parameters) / 2
    A = X
    
    # 1~ L-1 层，迭代
    for l in range(1,L):
        A_prev = A
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
        caches.append(cache)
        
    # L 层     
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
    caches.append(cache)
        
    # 验证
    assert(AL.shape == (1,X.shape[1]))

    return AL, caches

# 测试
def L_model_forward_test_case():
    """
    X = np.array([[-1.02387576, 1.12397796],
 [-1.62328545, 0.64667545],
 [-1.74314104, -0.59664964]])
    parameters = {'W1': np.array([[ 1.62434536, -0.61175641, -0.52817175],
        [-1.07296862,  0.86540763, -2.3015387 ]]),
 'W2': np.array([[ 1.74481176, -0.7612069 ]]),
 'b1': np.array([[ 0.],
        [ 0.]]),
 'b2': np.array([[ 0.]])}
    """
    np.random.seed(1)
    X = np.random.randn(4,2)
    W1 = np.random.randn(3,4)
    b1 = np.random.randn(3,1)
    W2 = np.random.randn(1,3)
    b2 = np.random.randn(1,1)
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return X, parameters

# 获取X和初始化参数
X, parameters = L_model_forward_test_case()

print "X.shape = " + str(X.shape) , "，即",X.shape[0],"行",X.shape[1],"列"

# 前向传播
AL, caches = L_model_forward(X, parameters)
print("AL = " + str(AL))
print("Length of caches list = " + str(len(caches)))
X.shape = (4L, 2L) ，即 4 行 2 列
AL = [[ 0.17007265  0.2524272 ]]
Length of caches list = 2

计算误差

误差公式如下：

\[-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right)) \tag{7}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def compute_cost(AL, Y):
    """
    实现公式7的误差计算
    
    输入：
    AL -- 上一步计算出的结果
    Y -- 实际的label
    
    Returns : 
    cost -- 交叉熵误差
    """
    
    m = Y.shape[1]
    
    # 计算
    cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m
    cost = np.squeeze(cost)
    
    # 验证
    assert(cost.shape == ())

    return cost
    
# 测试

def compute_cost_test_case():
    Y = np.asarray([[1, 1, 1]])
    aL = np.array([[.8,.9,0.4]])
    
    return Y, aL

Y, AL = compute_cost_test_case()

print("cost = " + str(compute_cost(AL, Y)))
cost = 0.414931599615

​

后向传播

后向传播是用来计算梯度的

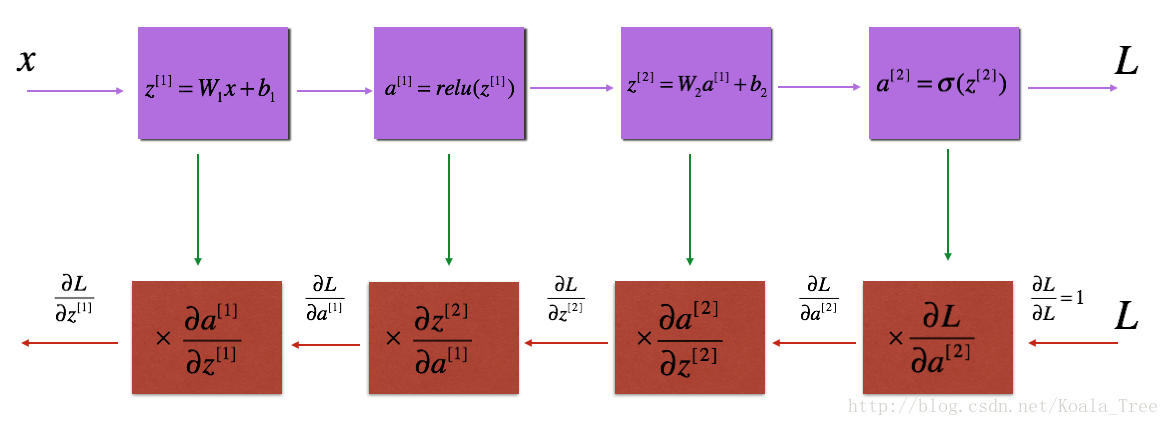
紫色方块代表前向传播 红色方块代表后向传播

我们的目标是计算出\(dw^{[l]}和db^{[l]}, l = 1,2,...L\)，以便之后更新w和b。

为了计算\(dw^{[1]}和db^{[1]}\)，要使用如下链式法则：

\(dw^{[1]}=\frac{dL}{dw^{[1]}}=\frac{dL}{dz^{[1]}} \times \frac{dz}{dw^{[1]}}=dz^{[1]}\times \frac{dz}{dw^{[1]}}\)

\(db^{[1]}=\frac{dL}{db^{[1]}} = \frac{dL}{dz^{[1]}} \times \frac{dz^{[1]}}{db^{[1]}} = dz^{[1]} \times \frac{dz^{[1]}}{db^{[1]}}\)

因此我们首先要算出\(dz^{[1]}\) :

\[\frac{dL(a^{[2]},y)}{dz^{[1]}}=\frac{dL(a^{[2]},y)}{da^{[2]}}\frac{da^{[2]}}{dz^{[2]}}\frac{dz^{[2]}}{da^{[1]}}\frac{da^{[1]}}{dz^{[1]}}\]

而要算出\(dz^{[1]}\)，由上公示可以看出，我们必须先计算\(dz^{[2]}\)等

因此此过程叫做后向传播

总之，后向传播需要完成： - LINEAR - LINEAR -> ACTIVATION - [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID backward (whole model)

LINEAR

对于第l层来说，这一层的Linear部分是：\(Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}\)

假设此时你已经计算好了 \(dZ^{[l]} = \frac{\partial \mathcal{L} }{\partial Z^{[l]}}\)

你接下来想要得到\((dW^{[l]}, db^{[l]} dA^{[l-1]})\)

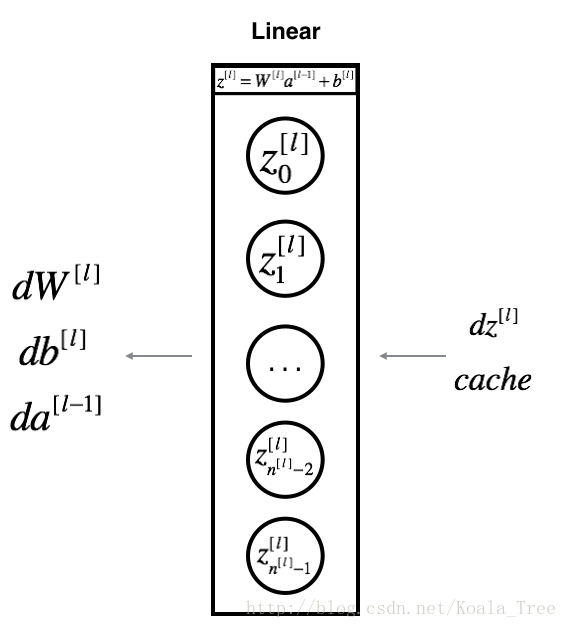
我们可以通过如下的公式，通过\(dZ^{[l]}\)来计算出这三个东西\((dW^{[l]}, db^{[l]}, dA^{[l-1]})\):

\[ dW^{[l]} = \frac{\partial \mathcal{L} }{\partial W^{[l]}} = \frac{1}{m} dZ^{[l]} A^{[l-1] T} \tag{8}\] \[ db^{[l]} = \frac{\partial \mathcal{L} }{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}\tag{9}\] \[ dA^{[l-1]} = \frac{\partial \mathcal{L} }{\partial A^{[l-1]}} = W^{[l] T} dZ^{[l]} \tag{10}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def linear_backward(dZ, cache):
    """
    实现后向传播的linear部分
    
    输入：
    dZ -- dL/dz
    cache -- 三元组(A_prev, W, b) , 来自于当前层的前向传播
    
    Returns:
    dA_prev -- 上一层A的梯度
    dW -- w的梯度
    db -- b的梯度
    """
    
    A_prev, W, b = cache
    m = A_prev.shape[1]
    
    # 计算dw，db，dA_prev
    dW = np.dot(dZ, A_prev.T) / m
    db = np.sum(dZ, axis = 1, keepdims = True) / m 
    dA_prev = np.dot(W.T, dZ) 
    
    # 验证
    assert (dA_prev.shape == A_prev.shape)
    assert (dW.shape == W.shape)
    assert (db.shape == b.shape)

    return dA_prev, dW, db
# 测试
def linear_backward_test_case():
    """
    z, linear_cache = (np.array([[-0.8019545 ,  3.85763489]]), (np.array([[-1.02387576,  1.12397796],
       [-1.62328545,  0.64667545],
       [-1.74314104, -0.59664964]]), np.array([[ 0.74505627,  1.97611078, -1.24412333]]), np.array([[1]]))
    """
    np.random.seed(1)
    dZ = np.random.randn(1,2)
    A = np.random.randn(3,2)
    W = np.random.randn(1,3)
    b = np.random.randn(1,1)
    linear_cache = (A, W, b)
    return dZ, linear_cache 

dZ, linear_cache = linear_backward_test_case()

dA_prev, dW, db = linear_backward(dZ, linear_cache)
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
dA_prev = [[ 0.51822968 -0.19517421]
 [-0.40506361  0.15255393]
 [ 2.37496825 -0.89445391]]
dW = [[-0.10076895  1.40685096  1.64992505]]
db = [[ 0.50629448]]

LINEAR -> ACTIVATION

本节要加入后向传播中的activation部分：

假设\(g(.)\)是激活函数，

而下面给出的两个函数：sigmoid_backward 和 relu_backward 计算了\(dL/dz\) : \[dZ^{[l]} = dA^{[l]} * g'(Z^{[l]}) \tag{11}\].

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def relu_backward(dA, cache):
    """
    Implement the backward propagation for a single RELU unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    
    Z = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.
    
    # When z <= 0, you should set dz to 0 as well. 
    dZ[Z <= 0] = 0
    
    assert (dZ.shape == Z.shape)
    
    return dZ

def sigmoid_backward(dA, cache):
    """
    Implement the backward propagation for a single SIGMOID unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    
    Z = cache
    
    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)
    
    assert (dZ.shape == Z.shape)
    
    return dZ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
def linear_activation_backward(dA, cache, activation):
    """
    后向传播的LINEAR->ACTIVATION实现
    
    输入：
    dA -- 当前层的输出A的导数
    cache -- 二元组(linear_cache, activation_cache)，也就是之前前向传播计算时的cache
    activation -- 本层的激活函数，是"sigmoid"或"relu"
    
    Returns :
    dA_prev -- 上一层输出的导数
    dW -- 本层W的导数
    db -- 本层b的导数
    """
    
    linear_cache, activation_cache = cache
    # 计算dZ
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA,activation_cache)
    # 已知dZ, 计算dA_prev, dW, db
    dA_prev, dW, db = linear_backward(dZ, linear_cache)
    
    return dA_prev, dW, db
# 测试
def linear_activation_backward_test_case():
    """
    aL, linear_activation_cache = (np.array([[ 3.1980455 ,  7.85763489]]), ((np.array([[-1.02387576,  1.12397796], [-1.62328545,  0.64667545], [-1.74314104, -0.59664964]]), np.array([[ 0.74505627,  1.97611078, -1.24412333]]), 5), np.array([[ 3.1980455 ,  7.85763489]])))
    """
    np.random.seed(2)
    dA = np.random.randn(1,2)
    A = np.random.randn(3,2)
    W = np.random.randn(1,3)
    b = np.random.randn(1,1)
    Z = np.random.randn(1,2)
    linear_cache = (A, W, b)
    activation_cache = Z
    linear_activation_cache = (linear_cache, activation_cache)
    
    return dA, linear_activation_cache

AL, linear_activation_cache = linear_activation_backward_test_case()

dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "sigmoid")
print ("sigmoid:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db) + "\n")

dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "relu")
print ("relu:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
sigmoid:
dA_prev = [[ 0.11017994  0.01105339]
 [ 0.09466817  0.00949723]
 [-0.05743092 -0.00576154]]
dW = [[ 0.10266786  0.09778551 -0.01968084]]
db = [[-0.05729622]]

(1L, 2L)
(1L, 2L)
relu:
dA_prev = [[ 0.44090989 -0.        ]
 [ 0.37883606 -0.        ]
 [-0.2298228   0.        ]]
dW = [[ 0.44513824  0.37371418 -0.10478989]]
db = [[-0.20837892]]

L-Model Backward

接下来就该将后向传播应用在整个网络了。步骤如下：

  1. 前向传播 - L_model_forward(),在每一层都存下了(X,W,b,z)
  2. 后向传播 - L_model_backward()，利用之前存的值，一层层向前计算导数

后向传播计算导数的流程如下图所示：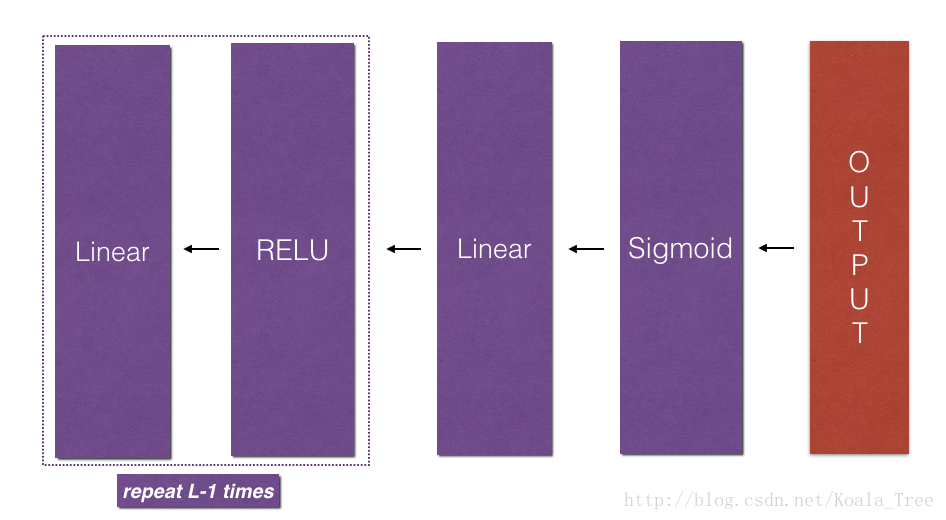

初始化部分

对于贯穿网络的后向传播来说，我们知道输出是\(A^{[L]} = \sigma(Z^{[L]})\). 我们需要计算出 ： dAL \(= \frac{\partial \mathcal{L}}{\partial A^{[L]}}\).

为了完成这个目标，我们用如下公式实现： 

1
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) # 相对于AL的成本衍生物
这个公式计算了LINEAR->SIGMOID后向传播部分

接下来就该计算LINEAR->RELU后向传播部分了，这一部分需要存储每一步的dA, dW, db，用如下公式实现： \[grads["dW" + str(l)] = dW^{[l]}\tag{15} \] 例如，l=3，就将dw3 存储在grads["dw3"]中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
def L_model_backward(AL, Y, chache):
    """
    [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID 的后向传播的实现
    
    输入：
    AL -- 概率向量，是前向传播L_model_forward()的输出
    Y  -- 标签向量
    caches -- caches列表：
                     1 ~ L - 1 : relu的linear_activation_forward()的caches
                     L         : sigmoid 的 linear_activation_forward()的caches
                     
    Returns:
    
    grads -- 梯度dict :
        grads["dA" + str(l)] = ...
        grads["dW" + str(l)] = ...
        grads["db" + str(l)] = ...
    """
    
    grads = {}
    L = len(caches)
    m = AL.shape[1]
    Y = Y.reshape(AL.shape)
    
    #后向传播的初始化
    dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) 
    
    # 计算dAL,dWL,dbL
    # 第L层 - (SIGMOID -> LINEAR)  - 的梯度
    # 输入 ：AL, Y, caches
    # 输出 ：grads["dAL"], grads["dWL"]
    current_cache = caches[L - 1]
    grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL,current_cache, "sigmoid")
    
    # 计算dAl,dWl,dbl , l = 1~L-1
    for l in reversed(range(L-1)):
        # 第l层：(RELU -> LINEAR) 的梯度
        # 输入 ： "grads["dA" + str(l + 2)], caches". 
        # 输出: "grads["dA" + str(l + 1)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)] 
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, "relu")
        grads["dA" + str(l + 1)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp
    return grads

# 测试
def L_model_backward_test_case():
    """
    X = np.random.rand(3,2)
    Y = np.array([[1, 1]])
    parameters = {'W1': np.array([[ 1.78862847,  0.43650985,  0.09649747]]), 'b1': np.array([[ 0.]])}

    aL, caches = (np.array([[ 0.60298372,  0.87182628]]), [((np.array([[ 0.20445225,  0.87811744],
           [ 0.02738759,  0.67046751],
           [ 0.4173048 ,  0.55868983]]),
    np.array([[ 1.78862847,  0.43650985,  0.09649747]]),
    np.array([[ 0.]])),
   np.array([[ 0.41791293,  1.91720367]]))])
   """
    np.random.seed(3)
    AL = np.random.randn(1, 2)
    Y = np.array([[1, 0]])

    A1 = np.random.randn(4,2)
    W1 = np.random.randn(3,4)
    b1 = np.random.randn(3,1)
    Z1 = np.random.randn(3,2)
    linear_cache_activation_1 = ((A1, W1, b1), Z1)

    A2 = np.random.randn(3,2)
    W2 = np.random.randn(1,3)
    b2 = np.random.randn(1,1)
    Z2 = np.random.randn(1,2)
    linear_cache_activation_2 = ( (A2, W2, b2), Z2)

    caches = (linear_cache_activation_1, linear_cache_activation_2)

    return AL, Y, caches

AL, Y_assess, caches = L_model_backward_test_case()
grads = L_model_backward(AL, Y_assess, caches)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dA1 = "+ str(grads["dA1"]))
(3L, 2L)
(3L, 2L)
dW1 = [[ 0.41010002  0.07807203  0.13798444  0.10502167]
 [ 0.          0.          0.          0.        ]
 [ 0.05283652  0.01005865  0.01777766  0.0135308 ]]
db1 = [[-0.22007063]
 [ 0.        ]
 [-0.02835349]]
dA1 = [[ 0.          0.52257901]
 [ 0.         -0.3269206 ]
 [ 0.         -0.32070404]
 [ 0.         -0.74079187]]

更新参数

在这一部分我们用以上模型更新参数：

\[ W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]} \tag{16}\] \[ b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]} \tag{17}\]

其中，\(\alpha\)是学习率。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
def update_parameters(parameters, grads, learning_rate):
    """
    用梯度下降更新参数
    
    输入：
    parameters -- python dict，里面包含一些参数
    grads -- python dict, 包含梯度
    
    Returns:
    parameters -- python dict, 包含更新后的参数：
                  parameters["W" + str(l)] = ... 
                  parameters["b" + str(l)] = ...
    """
    
    L = len(parameters) / 2
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]
    return parameters

# 测试

def update_parameters_test_case():
    """
    parameters = {'W1': np.array([[ 1.78862847,  0.43650985,  0.09649747],
        [-1.8634927 , -0.2773882 , -0.35475898],
        [-0.08274148, -0.62700068, -0.04381817],
        [-0.47721803, -1.31386475,  0.88462238]]),
 'W2': np.array([[ 0.88131804,  1.70957306,  0.05003364, -0.40467741],
        [-0.54535995, -1.54647732,  0.98236743, -1.10106763],
        [-1.18504653, -0.2056499 ,  1.48614836,  0.23671627]]),
 'W3': np.array([[-1.02378514, -0.7129932 ,  0.62524497],
        [-0.16051336, -0.76883635, -0.23003072]]),
 'b1': np.array([[ 0.],
        [ 0.],
        [ 0.],
        [ 0.]]),
 'b2': np.array([[ 0.],
        [ 0.],
        [ 0.]]),
 'b3': np.array([[ 0.],
        [ 0.]])}
    grads = {'dW1': np.array([[ 0.63070583,  0.66482653,  0.18308507],
        [ 0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ]]),
 'dW2': np.array([[ 1.62934255,  0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ,  0.        ]]),
 'dW3': np.array([[-1.40260776,  0.        ,  0.        ]]),
 'da1': np.array([[ 0.70760786,  0.65063504],
        [ 0.17268975,  0.15878569],
        [ 0.03817582,  0.03510211]]),
 'da2': np.array([[ 0.39561478,  0.36376198],
        [ 0.7674101 ,  0.70562233],
        [ 0.0224596 ,  0.02065127],
        [-0.18165561, -0.16702967]]),
 'da3': np.array([[ 0.44888991,  0.41274769],
        [ 0.31261975,  0.28744927],
        [-0.27414557, -0.25207283]]),
 'db1': 0.75937676204411464,
 'db2': 0.86163759922811056,
 'db3': -0.84161956022334572}
    """
    np.random.seed(2)
    W1 = np.random.randn(3,4)
    b1 = np.random.randn(3,1)
    W2 = np.random.randn(1,3)
    b2 = np.random.randn(1,1)
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    np.random.seed(3)
    dW1 = np.random.randn(3,4)
    db1 = np.random.randn(3,1)
    dW2 = np.random.randn(1,3)
    db2 = np.random.randn(1,1)
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return parameters, grads

parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)

print ("W1 = "+ str(parameters["W1"]))
print ("b1 = "+ str(parameters["b1"]))
print ("W2 = "+ str(parameters["W2"]))
print ("b2 = "+ str(parameters["b2"]))
W1 = [[-0.59562069 -0.09991781 -2.14584584  1.82662008]
 [-1.76569676 -0.80627147  0.51115557 -1.18258802]
 [-1.0535704  -0.86128581  0.68284052  2.20374577]]
b1 = [[-0.04659241]
 [-1.28888275]
 [ 0.53405496]]
W2 = [[-0.55569196  0.0354055   1.32964895]]
b2 = [[-0.84610769]]