大纲
有序数组
子数组
Two Sum
Two Pointers
有序数组
例题1,Merge Two Sorted Array
将两个有序数组合并,A = [1,2,3,empty,empty],B = [4,5]。将B合并到A里
思路:从最大的开始放
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public void merge (int [] nums1, int m, int [] nums2, int n) int pos = m + n - 1 ; --m;--n; while (m >= 0 && n >= 0 ){ if (nums1[m] > nums2[n]){ nums1[pos] = nums1[m]; --m; }else { nums1[pos] = nums2[n]; --n; } --pos; } while (n >= 0 ){ nums1[pos] = nums2[n]; --n; --pos; } }
例题2,Intersection of Two Arrays, leetcode 349
求两个数组的交集
思路:先排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 代码 public int [] intersection(int [] nums1, int [] nums2) { Arrays.sort(nums1); Arrays.sort(nums2); int head1 = 0 ,head2 = 0 ; List<Integer> result = new LinkedList<>(); int counter = 0 ; while (head1 < nums1.length && head2 < nums2.length){ if (nums1[head1] == nums2[head2]){ result.add(nums1[head1]); ++counter; int temp = nums1[head1]; while (head1 < nums1.length && nums1[head1] == temp){ ++head1; } while (head2 < nums2.length && nums2[head2] == temp){ ++head2; } }else if (nums1[head1] < nums2[head2]){ ++head1; }else { ++head2; } } int [] resArr = new int [counter]; int i = 0 ; for (Integer ele : result){ resArr[i] = ele; ++i; } return resArr; }
Intersection of Two Arrays II
求两个数组的交集,交集不用去重
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int [] intersect(int [] nums1, int [] nums2) { Arrays.sort(nums1); Arrays.sort(nums2); int head1 = 0 ,head2 = 0 ; List<Integer> result = new LinkedList<>(); int counter = 0 ; while (head1 < nums1.length && head2 < nums2.length){ if (nums1[head1] == nums2[head2]){ result.add(nums1[head1]); ++counter; ++head1; ++head2; }else if (nums1[head1] < nums2[head2]){ ++head1; }else { ++head2; } } int [] resArr = new int [counter]; int i = 0 ; for (Integer ele : result){ resArr[i] = ele; ++i; } return resArr; }
几个follow up:
如果数组有序——那简直太完美了
如果nums1很短,怎样优化会好些?
如果nums2存储在磁盘中,内存限制不能一次性读取全部,怎么办?
如果只有nums2太大,那就把nums1放在一个hash表里,然后一块块读取nums2,依次匹配交集
如果两个数组都很大,那就只能先排序,然后再依次读取了
例题3,点乘
数组内积(点乘)FOLLOW UP: 两个数组都非常大,但是其中都包含很多0
首先改变存储,因为0特别多,所以只存储非0元素的下标和数值。 计算内积的时候,只有下标都出现的数值相乘才有值,所以要计算两个数组的下标的交集,最后把值算出来。 所以本问题就转变成了求两个数组交的问题了。
Sparse Matrix Multiplication
求稀疏矩阵的乘法
然而这种方式依然很慢。其实直接遍历就可以了。我们知道一个 i x k 的矩阵A乘以一个 k x j 的矩阵B会得到一个 i x j 大小的矩阵C,那么我们来看结果矩阵中的某个元素C[i][j]是怎么来的,起始是A[i][0]*B[0][j] + A[i][1]*B[1][j] + ... + A[i][k]*B[k][j],直观地写成代码就是:
1 2 3 4 5 6 7 for (int i = 0 ; i < row ; ++i){ for (int j = 0 ; j < col; ++j) { for (int k = 0 ; k < A[0 ].length ; ++k) { result[i][j] += A[i][k]*B[k][j]; } } }
然而如果有很多0的话,必然会导致大量的0的乘法。这是会超时的。
就算我们这么写:
1 2 3 4 5 6 7 8 9 for (int i = 0 ; i < row ; ++i){ for (int j = 0 ; j < col; ++j) { for (int k = 0 ; k < A[0 ].length ; ++k) { if (A[i][k] != 0 && B[k][j] !=0 ) { result[i][j] += A[i][k] * B[k][j]; } } } }
这虽然能过,但beats 1.75%,非常的慢。
那么为了不重复计算0乘0,我们将遍历顺序变一下。首先遍历A数组,要确保A[i][k]不为0,才继续计算,然后我们遍历B矩阵的第k行,如果B[K][J]不为0,我们累加结果矩阵res[i][j] += A[i][k] * B[k][j]; 这样我们就能高效的算出稀疏矩阵的乘法,参见代码如下:
哇快了有十倍!可以说是相当的机制了。
(仔细多想想,究竟省去了什么,才变得这么快?)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int [][] multiply(int [][] A, int [][] B) { if (A.length == 0 || A[0 ].length == 0 || B.length == 0 || B[0 ].length == 0 ) return null ; int row = A.length , col = B[0 ].length ; int [][] result = new int [row][col]; for (int i = 0 ; i < row ; ++i){ for (int k = 0 ; k < A[0 ].length ; ++k) { if (A[i][k] == 0 ) continue ; for (int j = 0 ; j < col; ++j) { if (B[k][j] ==0 ) continue ; result[i][j] += A[i][k] * B[k][j]; } } } return result; }
另一种思路 :借用上一题的思路,建立A的每行的非零元素和B的每列的非零元素的索引。然后再乘。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 class ListNode int val; ListNode next; ListNode(int val){ this .val = val; } } public int [][] multiply(int [][] A, int [][] B) { if (A.length == 0 || A[0 ].length == 0 || B.length == 0 || B[0 ].length == 0 ) return null ; ListNode[] index_A = new ListNode[A.length]; for (int i = 0 ; i < A.length ; ++i){ ListNode dummy = new ListNode(0 ); ListNode curr = dummy; for (int j = 0 ; j < A[i].length ; ++j){ if (A[i][j] != 0 ) { ListNode next = new ListNode(j); curr.next = next; curr = next; } } index_A[i] = dummy.next; } ListNode[] index_B = new ListNode[B[0 ].length]; for (int j = 0 ; j < B[0 ].length ; ++j){ ListNode dummy = new ListNode(0 ); ListNode curr = dummy; for (int i = 0 ; i < B.length ; ++i){ if (B[i][j] != 0 ){ ListNode next = new ListNode(i); curr.next = next; curr = next; } } index_B[j] = dummy.next; } int row = A.length , col = B[0 ].length ; int [][] result = new int [row][col]; for (int i = 0 ; i < row ; ++i){ for (int j = 0 ; j < col ; ++j){ result[i][j] = getSum(i,j,A,B,index_A,index_B); } } return result; } private int getSum (int row,int col, int [][] A,int [][] B, ListNode[] index_A, ListNode[] index_B) ListNode curr_A = index_A[row]; ListNode curr_B = index_B[col]; int sum = 0 ; while (null != curr_A && null != curr_B){ if (curr_A.val == curr_B.val){ sum += A[row][curr_A.val]*B[curr_A.val][col]; curr_A = curr_A.next; curr_B = curr_B.next; }else if (curr_A.val < curr_B.val){ curr_A = curr_A.next; }else { curr_B = curr_B.next; } } return sum; }
例题5,Kth Largest Element
一个数组的第k大数
之前有一个实现方法,用堆。复杂度是\(O(nlogk)\)
这次使用快速选择,复杂度是\(O(n)\)
思路:
快速选择
Quick select算法因其高效和良好的average case时间复杂度而被广为应用。Quick select的average case时间复杂度为O(n),然而其worst case时间复杂度为O(n^2)。总体而言,Quick select采用和Quick sort类似的步骤。首先选定一个pivot,然后根据每个数字与该pivot的大小关系将整个数组分为两部分。那么与Quick sort不同的是,Quick select只考虑所寻找的目标所在的那一部分子数组,而非像Quick sort一样分别再对两边进行分割。正是因为如此,Quick select将平均时间复杂度从O(nlogn)降到了O(n)。
步骤:
从数列中挑出一个元素,称为”基准”(pivot)。
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。
判断第k个最小元素位于左侧还是右侧,然后对该侧进行递归。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 过程 假设寻找第k=3 大的元素,也就是找第6 - 3 + 1 = 4 小的元素 , 也就是7 为了方便起见,我们下面的index都是从1 开始 i j ↓ ↓ 1 2 3 4 5 6 2 , 1 , 7 , 8 , 9 , 4 pivot = 7 ++i 两次 i j 2 , 1 , 7 , 8 , 9 , 4 交换i,j,并++i,--j i j 2 , 1 , 4 , 8 , 9 , 7 --j j i 2 , 1 , 4 , 8 , 9 , 7 总之,通过加加减减交换,以上数组变为 j i ↓ ↓ 1 2 3 4 5 6 2 , 1 , 4 , 8 , 9 , 7 pivot = 7 此时j<i,跳出while 循环 此时: - [1 ,j]的元素都小于pivot - [i,n]的元素都大于pivot 然后看第k小的元素是在左边还是右边: - 如果在左边,那k <= j - 如果在右边,那k >= i 我们发现 k >= i (4 >= 4 ),那就再在右边找: ===================================== i j ↓ ↓ 1 2 3 4 5 6 2 , 1 , 4 , 8 , 9 , 7 pivot = 9 通过加加减减交换,以上数组变为 j i ↓ ↓ 1 2 3 4 5 6 2 , 1 , 4 , 8 , 7 , 9 pivot = 9 此时j<i,跳出while 循环 然后看第k小的元素是在左边还是右边: - 如果在左边,那k <= j - 如果在右边,那k >= i 我们发现 k <= j (4 <= 5 ),那就继续向右边寻找 ===================================== j,i ↓ 1 2 3 4 5 6 2 , 1 , 4 , 8 , 7 , 9 此时j == i ,直接输出7 而在代码中,idx从0 开始,因此直接给k-1 即可 参考代码: public int kthLargestElement (int k, int [] nums) return quickSelece(nums,0 ,nums.length - 1 , nums.length - k + 1 ); } private int quickSelect (int [] nums, int start, int end, int k) if (start == end){ return nums[start]; } int mid = start + (end - start)/2 ; int pivot = nums[mid]; int i = start, j = end; while (i <= j){ while (i <= j && nums[i] < pivot){ i++; } while (i <= j && nums[j] > pivot){ j--; } if (i <= j){ int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; i++; j--; } } if (start + k - 1 <= j){ return quickSelect(nums, start, i, k); } if (start + k - 1 >= i){ return quickSelect(nums, i, end, k - (i - start)); } return nums[j + 1 ]; } 代码: public int findKthLargest (int [] nums, int k) if (nums.length == 0 ) return -1 ; return quickSelect(0 ,nums.length - 1 ,nums,nums.length - k); } private int quickSelect (int start, int end, int [] nums, int k) if (start == end){ return nums[start]; } int mid = start + (end - start) / 2 ; int pivot = nums[mid]; int i = start,j = end; while (i <= j){ while (i <= j && nums[i] < pivot){ ++i; } while (i <= j && nums[j] > pivot){ --j; } if (i <= j){ int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; ++i; --j; } } if (k <= j){ return quickSelect(start,j,nums,k); }else if (k >= i){ return quickSelect(i,end,nums,k); }else { return pivot; } }
二刷:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 public int findKthLargest (int [] nums, int k) if (nums.length == 0 ) return 0 ; if (nums.length == 1 ) return nums[0 ]; this .nums = nums; this .k = nums.length - k; return quickSelect(); } int [] nums;int k;private int quickSelect () int low = 0 , high = nums.length - 1 ; while (low < high) { int emptyIdx = low; int pivot = nums[emptyIdx]; int i = low, j = high; while (i < j) { while (i < j && nums[j] >= pivot) { --j; } if (nums[j] < pivot) { nums[emptyIdx] = j; emptyIdx = j; } while (i < j && nums[i] <= pivot) { ++i; } if (nums[i] > pivot){ nums[emptyIdx] = i; emptyIdx = i; } } int pivotIdx = emptyIdx; if (pivotIdx == k) { return nums[pivotIdx]; } if (pivotIdx > k) { high = pivotIdx - 1 ; } else { low = pivotIdx + 1 ; } } if (low == high) { if (low == k) return nums[low]; else return 0 ; } return 0 ; }
两个排序数组的中位数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 思路,先找Kth 小,与之前链表的题思路差不多 A[k/2 ] <B[k/2 ] -> 先丢掉前A[k/2 ] public static int findKth (int [] A, int A_start, int [] B, int B_start, int k) if (A_start >= A.length){ return B[B_start + k - 1 ]; } if (B_start >= B.length){ return A[A_start + k - 1 ]; } if ( k == 1 ){ return Math.min(A[A,start], B_[B_start]); } int A_key = A_start + k/2 <= A.length ? A[A_start + k/2 - 1 ] : Interger.MAX_VALUE; int B_key = B_start + k/2 <= B.length ? B[B_start + k/2 - 1 ] : Interger.MAX_VALUE; if (A_key < B_key){ return findKth(A, start + k/2 , B, B_start, k - k/2 ); }else { return findKth(A, start, B, B_start + k/2 , k - k/2 ); } } 这道题在二分法里面讲过了 二刷! public static int findKth (int [] A, int A_start, int [] B, int B_start, int k) if (A_start >= A.length){ return B[B_start + k]; } if (B_start >= B.length){ return A[A_start + k]; } if (k == 0 ) return Math.min(A[A_start],B[B_start]); if (k == 1 ){ if (A[A_start] > B[B_start]){ return findKth(A,A_start,B,B_start+1 ,0 ); }else { return findKth(A,A_start+1 ,B,B_start,0 ); } } if (A_start + k/2 >= A.length){ if (A[A.length - 1 ] > B[B_start + k/2 ]){ return findKth(A,A_start,B,B_start + k/2 , k - k/2 ); }else { k -= A.length - A_start; return findKth(A,A.length,B,B_start,k); } } if (B_start + k/2 >= B.length){ if (B[B.length - 1 ] > A[A_start + k/2 ]){ return findKth(A,A_start + k/2 ,B,B_start, k - k/2 ); }else { k -= B.length - B_start; return findKth(A,A_start,B,B.length,k); } } if (A[A_start + k/2 ] > B[B_start + k/2 ]){ return findKth(A,A_start,B,B_start + k/2 , k - k/2 ); }else { return findKth(A,A_start + k/2 ,B,B_start, k - k/2 ); } } public double findMedianSortedArrays (int [] nums1, int [] nums2) if (nums1.length == 0 && nums2.length == 0 ){ return -1 ; } int total = nums1.length + nums2.length; if (total%2 == 0 ){ double a = findKth(nums1,0 ,nums2,0 ,total/2 - 1 ); double b = findKth(nums1,0 ,nums2,0 ,total/2 ); return (a + b)/2 ; }else { return findKth(nums1,0 ,nums2,0 ,total/2 ); } }
Find the Duplicate Number
给n+1个数,数的值为1~n。有且只有一个数有重复。返回这个重复的数。
思路:利用下标。
1 2 3 4 5 6 7 8 9 10 public int findDuplicate (int [] nums) if (nums.length <= 0 )return -1 ; int idx; for (int i = 0 ; i < nums.length; ++i){ idx = Math.abs(nums[i]); if (nums[idx] < 0 )return idx; nums[idx] = -nums[idx]; } return -1 ; }
Remove Duplicates from Sorted Array II
从数组中去除重复次数大于2的数字,并返回去重后的长度
边界条件啊!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int removeDuplicates (int [] nums) if (nums.length <= 2 ) return nums.length; int last = nums[0 ]; int lastCounter = 1 ; int length = nums.length; int step = 0 ; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] == last){ ++lastCounter; if (lastCounter > 2 ){ ++step; --length; --i; } }else { last = nums[i]; lastCounter = 1 ; } if (i + 1 + step >= nums.length) break ; nums[i + 1 ] = nums[i + 1 + step]; } return length; }
快慢指针!骚操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 fast -- 第一个新的数字 slow -- 之前都是去重了的 public int removeDuplicates (int [] nums) if (nums == null || nums.length <= 2 ) { return nums.length; } int slow = 2 ; for (int fast = 2 ; fast < nums.length; fast++) { if (nums[fast] != nums[slow-2 ]) { nums[slow++] = nums[fast]; } } return slow; }
Reverse Pairs
定义逆序对为if i < j and nums[i] > 2*nums[j] 。找到一个数组的所有逆序对个数。
归并思路
为了方便分析,我们先简化问题:if i < j and nums[i] > nums[j] 为逆序对。那么:
利用mergetSort的性质,即将数组分为左右两个子数组,左边数组元素index都小于右边数组元素index,同时在merge的时候会挨个比较左右两个数组元素大小,此时只要左边数组某一个元素i大于右边数组某一个元素j,则从i开始到左边数组最后一个元素和j都是reverse pairs的关系。因此,每一次merge都能寻找reverse pairs。对于每一次切割,其reverse pairs为左边数组merge找到的reverse pairs的个数 + 右边数组merge找到的reverse pairs的个数 + 左右数组merge找到的reverse pairs的个数。
回到本问题的逆序对,既然需要nums[i] > 2*nums[j] ,那么就绝对不可以在归并的同时进行数数!【这个bug我找了一整天】,比如[-199]和[-198,-197] 归并时,虽然-197比较大,但是不可以忽略!所以必须先数数,再归并!
一个简短的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public class Solution public int ret; public int reversePairs (int [] nums) ret = 0 ; mergeSort(nums, 0 , nums.length-1 ); return ret; } public void mergeSort (int [] nums, int left, int right) if (right <= left) { return ; } int middle = left + (right - left)/2 ; mergeSort(nums, left, middle); mergeSort(nums,middle+1 , right); int count = 0 ; for (int l = left, r = middle+1 ; l <= middle;) { if (r > right || (long )nums[l] <= 2 *(long )nums[r]) { l++; ret += count; } else { r++; count++; } } Arrays.sort(nums, left, right + 1 ); } }
子数组问题
例题7,Maximum Subarray
求一个数组的最大的连续子数组和。
转化:前缀和。最大子数组就是股票问题!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 sum[i] = sum(nums[0 ~ i]) sum[i~j] = sum[j] - sum[i] 参考程序: public int maxSubArray (int [] A) if (A == null || A.length == 0 ){ return 0 ; } int max = Integer.MIN_VALUE, sum = 0 , minSum = 0 ; for (int i = 0 ; i < A.length; i++){ sum += A[i]; max = Math.max(max, sum - minSum); minSum = Math.min(minSum, sum); } return max; } 自己的另一种思路: public int maxSubArray (int [] nums) int maxLast = 0 ; int max = Integer.MIN_VALUE; for (int i = 0 ; i < nums.length ; ++i){ maxLast = Math.max(maxLast + nums[i],nums[i]); max = Math.max(maxLast,max); } return max; }
例题8,二维数组的Maximum Subarray
前缀和
1 2 3 4 5 6 7 8 9 10 11 12 13 i-1 i x *---*---*---*---* | | | | | j-1 *---*---*---*---* | | | | | j *-[i,j]-*---*---* | | | | | *---*---*---*---* | | | | | y *---*---*---*-[x,y] sum[i,j - x,y] = sum[x,y] - sum[x,j-1 ] - sum[i-1 ,y] + sum[i-1 ,j-1 ]
Range Sum Query 2D - Immutable
给一个二维数组,定义(row1,col1)到(row2,col2)的矩阵的和时sumRegion(row1,col1,row2,col2);求任意的两点之间的和。
样例:
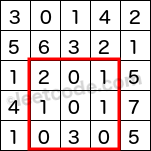
1 2 3 4 5 6 7 8 9 10 11 12 Given matrix = [ [3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5] ] sumRegion(2, 1, 4, 3) -> 8 sumRegion(1, 1, 2, 2) -> 11 sumRegion(1, 2, 2, 4) -> 12
与样题思路差不多。先将sum存下来,然后再计算sumRegion
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public class NumMatrix int [][] matrix; int [][] sum; int n; int m; public NumMatrix (int [][] matrix) if (matrix.length == 0 || matrix[0 ].length == 0 ) return ; this .matrix = matrix; n = matrix.length; m = matrix[0 ].length; sum = new int [n][m]; sum[0 ][0 ] = matrix[0 ][0 ]; for (int i = 1 ; i < n; ++i){ sum[i][0 ] = sum[i-1 ][0 ] + matrix[i][0 ]; } for (int j = 1 ; j < m; ++j){ sum[0 ][j] = sum[0 ][j-1 ] + matrix[0 ][j]; } for (int i = 1 ; i < n; ++i){ for (int j = 1 ; j < m; ++j){ sum[i][j] = sum[i-1 ][j] + sum[i][j-1 ] - sum[i-1 ][j-1 ] + matrix[i][j]; } } } public int sumRegion (int row1, int col1, int row2, int col2) if (row1 == 0 && col1 == 0 ) return sum[row2][col2] ; if (row1 == 0 ){ return sum[row2][col2] - sum[row2][col1 - 1 ] ; } if (col1 == 0 ){ return sum[row2][col2] - sum[row1 - 1 ][col2] ; } return sum[row2][col2] - sum[row1 - 1 ][col2] - sum[row2][col1 - 1 ] + sum[row1-1 ][col1-1 ]; } }
Range Sum Query 2D - Mutable
将上一题加一个条件,随时都有可能改变matrix中的某个值。
我们只需要加一个public void update(int row, int col, int val)即可。
1 2 3 4 5 6 7 8 9 10 public void update (int row, int col, int val) int cha = val - matrix[row][col] ; if (cha == 0 ) return ; matrix[row][col] = val; for (int i = row ; i < n; ++i){ for (int j = col; j < m; ++j){ sum[i][j] += cha; } } }
例题10,Minimum Subarray
最小子数组
转化:将所有数字取相反数,取最大即可
Minimum Size Subarray Sum
给一个数组和一个s,求连续子数组和大于等于的最小长度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 我的思路: 0 ,1 ,....,i,...,j对于每个j,从j到0 遍历i,当i-j的和大于等于s时,当前长度为j-i,与全局最小长度作比较,取最小值。 public int minSubArrayLen (int s, int [] nums) if (nums.length == 0 ) return 0 ; for (int i = 1 ; i < nums.length; ++i){ nums[i] = nums[i-1 ] + nums[i]; } int minLen = Integer.MAX_VALUE; for (int i = 0 ; i < nums.length; ++i){ if (nums[i] >= s){ minLen = Math.min(i + 1 , minLen); } for (int j = i - 1 ; j>= 0 ; --j){ if (nums[i] - nums[j] >= s){ minLen = Math.min(minLen, i - j); break ; } } } return minLen == Integer.MAX_VALUE ? 0 : minLen; }
然而这种方式很慢,复杂度大约为\(O(n^2)\)
上面这种方式有一个二分法的优化,复杂度为\(O(nlogn)\)
以上代码中,nums[i]表示[0,i-1]的和。而原nums都是正数,因此nums是递增的。对于每一个i,用二分查找法找到子数组的右边界j的位置,使子数组[i,j]之和大于 s,然后我们更新最短长度的距离即可
然而,重点在于sum[i,j] = nums[j]-nums[i-1],我们可以采取巧妙的操作:
1 2 3 nums[j] - nums[i - 1 ] >= s ↓ 变为 nums[j] >= s + nums[i-1 ]
即,只需要找一个nums[j],使得它大于等于s+nums[i-1]即可!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 int [] nums; public int minSubArrayLen (int s, int [] nums) if (nums.length == 0 ) return 0 ; for (int i = 1 ; i < nums.length; ++i){ nums[i] = nums[i-1 ] + nums[i]; } this .nums = nums; int minLen = Integer.MAX_VALUE; for (int i = 0 ; i < nums.length; ++i){ int j = bitSearch(nums,i,nums.length - 1 , s + getNums(i-1 )); minLen = Math.min(minLen, j - i + 1 ); } return minLen == Integer.MAX_VALUE ? 0 : minLen; } private int getNums (int i) if (i == -1 ){ return 0 ; }else { return nums[i]; } } private int bitSearch (int [] nums, int start, int end, int target) while (start + 1 < end){ int mid = start + (end - start)/2 ; if (getNums(mid) >= target){ end = mid; }else { start = mid; } } if (getNums(start) >= target) return start; if (getNums(end) >= target) return end; return Integer.MAX_VALUE; }
居然还有更骚的操作:滑动窗口解法,复杂度为\(O(n)\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int minSubArrayLen (int s, int [] nums) if (nums.length == 0 ) return 0 ; int minLen = Integer.MAX_VALUE; int i = 0 , j = 0 ; int windowSum = 0 ; while (j < nums.length){ while (j < nums.length && windowSum < s){ windowSum += nums[j]; ++j; } while (i < j && s >= windowSum){ minLen = Math.min(minLen, j - i + 1 ); windowSum -= nums[i]; ++i; } } return minLen == nums.length + 1 ? 0 : minLen; }
例题11,Maximum Subarray II
求两个不重叠子数组,使他们和最大
思路:一条分割线,求左右的最大maxSub,然后相加。然后求全局的最大。
优化:移动的时候,左边的maxArray并不需要重新计算!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public int maxTwoSubArrays (List<Integer> nums) if (null == nums)return -1 ; int n = nums.size(); if (n == 0 ) return -1 ; if (n == 1 ) return nums.get(0 ); int [] maxBefore = new int [n]; maxBefore[0 ] = nums.get(0 ); int lastMax = maxBefore[0 ]; for (int i = 1 ; i < n; ++i){ lastMax = Math.max(lastMax + nums.get(i), nums.get(i)); maxBefore[i] = Math.max(maxBefore[i-1 ],lastMax); } int [] maxAfter = new int [n]; maxAfter[n-1 ] = nums.get(n-1 ); lastMax = maxAfter[n-1 ]; for (int i = n - 2 ; i >= 0 ; --i){ lastMax = Math.max(lastMax + nums.get(i), nums.get(i)); maxAfter[i] = Math.max(maxAfter[i+1 ],lastMax); } int max = Integer.MIN_VALUE; for (int i = 0 ; i < n - 1 ; ++i){ max = Math.max(max, maxBefore[i] + maxAfter[i+1 ]); } return max; }
例题12,Max Subarray Difference
求两个不重叠子数组,使他们绝对值最大
与上一题思路相似
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public int maxDiffSubArrays (int [] nums) int n = nums.length; int [] maxBefore = new int [n]; int [] minBefore = new int [n]; maxBefore[0 ] = nums[0 ]; minBefore[0 ] = nums[0 ]; int lastMax = nums[0 ]; int lastMin = nums[0 ]; for (int i = 1 ; i < n ; ++i){ lastMax = Math.max(lastMax + nums[i], nums[i]); lastMin = Math.min(lastMin + nums[i], nums[i]); maxBefore[i] = Math.max(maxBefore[i-1 ] , lastMax); minBefore[i] = Math.min(minBefore[i-1 ] , lastMin); } int [] maxAfter = new int [n]; int [] minAfter = new int [n]; maxAfter[n-1 ] = nums[n-1 ]; minAfter[n-1 ] = nums[n-1 ]; lastMax = nums[n-1 ]; lastMin = nums[n-1 ]; for (int i = n - 2 ; i >= 0 ; --i){ lastMax = Math.max(lastMax + nums[i], nums[i]); lastMin = Math.min(lastMin + nums[i], nums[i]); maxAfter[i] = Math.max(maxAfter[i+1 ] , lastMax); minAfter[i] = Math.min(minAfter[i+1 ] , lastMin); } int max = Integer.MIN_VALUE; for (int i = 0 ; i < n - 1 ; ++i){ max = Math.max(max, Math.abs(maxBefore[i] - minAfter[i+1 ])); max = Math.max(max, Math.abs(minBefore[i] - maxAfter[i+1 ])); } return max; }
例题13,Subarray Sum
求一个子数组的和为0的子数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 一开始思路很暴力,就直接用前缀数组来求每个sum[i,j],然后与0 比较。然而,超时了 public List<Integer> subarraySum (int [] nums) int n = nums.length; List<Integer> result = new LinkedList<>(); if (n == 0 ) return result; if (nums[0 ] == 0 ) { result.add(0 );result.add(0 ); return result; } for (int i = 1 ; i < nums.length; ++i){ nums[i] += nums[i-1 ]; } for (int i = n-1 ; i >=0 ; --i){ if (nums[i] == 0 ){ result.add(0 );result.add(i); return result; } for (int j = i; j < n; ++j){ if (nums[j] - nums[i-1 ] == 0 ){ result.add(i); result.add(j); return result; } } } return result; }
改进:哈希表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 根据给的例子:[-3 , 1 , 2 , -3 , 4 ],其累加和: nums [-3 , 1 , 2 , -3 , 4 ] 0 1 2 3 4 sum [-3 ,-2 , 0 , -3 , 1 ] i j 1. i=2 出现了一个数0 -> sum[0 ,i] = 0 ,是一个答案2. 同时在i,j发现两个-3 -> sum[i+1 ,j] = 0 ,是一个答案代码: public List<Integer> subarraySum (int [] nums) int n = nums.length; List<Integer> result = new LinkedList<>(); if (n == 0 ) return result; if (nums[0 ] == 0 ) { result.add(0 );result.add(0 ); return result; } HashMap<Integer,Integer> set = new HashMap<>(); set.put(nums[0 ],0 ); for (int i = 1 ; i < nums.length; ++i){ if (nums[i] == 0 ){ result.add(i);result.add(i); return result; } nums[i] += nums[i-1 ]; if (nums[i] == 0 ){ result.add(0 );result.add(i); return result; } if (set.containsKey(nums[i])){ result.add(set.get(nums[i]) + 1 ); result.add(i); return result; } set.put(nums[i],i); } return result; }
##例题14, Subarray Sum Closest
求一个数组的子数组最接近0的子数组
一开始想法依然很暴力,但超时了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public int [] subarraySumClosest(int [] nums) { int n = nums.length; int [] ans = new int [2 ]; int min = Math.abs(nums[0 ]); if (n == 0 ) return ans; for (int i = 1 ; i < n; ++i){ nums[i] += nums[i-1 ]; if (Math.abs(nums[i]) < min){ min = Math.abs(nums[i]); ans[0 ] = 0 ; ans[1 ] = i; } } for (int i = 1 ; i < n; i++){ for (int j = i; j < n; ++j){ if (Math.abs(nums[j] - nums[i-1 ]) < min){ min = Math.abs(nums[j] - nums[i-1 ]); ans[0 ] = i; ans[1 ] = j; } } } return ans; }
思路:对前缀和排序,然后for
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class PreSum implements Comparable <PreSum > int sum; int idx; PreSum(int sum, int idx){ this .sum = sum; this .idx = idx; } @Override public int compareTo (PreSum o) return this .sum - o.sum; } } public int [] subarraySumClosest(int [] nums) { int n = nums.length; int [] ans = new int [2 ]; PreSum[] preSum = new PreSum[n]; if (n <= 1 ) return ans; int sum = nums[0 ]; preSum[0 ] = new PreSum(sum,0 ); for (int i = 1 ; i < n; ++i){ sum += nums[i]; preSum[i] = new PreSum(sum,i); } Arrays.sort(preSum); int min = Math.abs(nums[0 ]); for (int i = 1 ;i < n; ++i){ if (min > preSum[i].sum - preSum[i-1 ].sum){ min = preSum[i].sum - preSum[i-1 ].sum; ans[0 ] = preSum[i-1 ].idx; ans[1 ] = preSum[i].idx; } } if (ans[0 ] > ans[1 ]){ int temp = ans[0 ]; ans[0 ] = ans[1 ]; ans[1 ] = temp; } ans[0 ] += 1 ; return ans; }
Contiguous Array
给一个数组,元素是1或0。求子数组的最大长度。要求子数组的1和0个数相等。
思路一:(会超memory)
如果[i,j]的1和0个数相等,则sum(i,j) *2 = j - i +1
用dp[i][j]存储子数组[i,j]是否是1和0个数相等
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 int [][] dp; private int find (int [] nums,int start, int end) if (end == start) return 0 ; if (dp[start][end] != 0 ) return dp[start][end]; int sum; if (start == 0 ){ sum = nums[end]; }else { sum = nums[end] - nums[start - 1 ]; } int n = end - start + 1 ; if (n%2 == 0 && sum*2 == n){ dp[start][end] = n; }else { dp[start][end] = Math.max(find(nums,start+1 ,end), find(nums,start,end-1 )); } return dp[start][end]; } public int findMaxLength (int [] nums) if (nums.length <= 1 ) return 0 ; dp = new int [nums.length][nums.length]; for (int i = 1 ; i < nums.length; ++i){ nums[i] += nums[i-1 ]; } return find(nums,0 ,nums.length - 1 ); }
思路二,骚操作:
将0替换为-1.那这道题就转化为了求最长子数组,子数组和为0。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int findMaxLength (int [] nums) if (nums.length <= 1 ) return 0 ; for (int i = 0 ; i < nums.length; ++i){ if (nums[i] == 0 )nums[i] = -1 ; } HashMap<Integer,Integer> hash = new HashMap<>(); int sum = 0 ; int maxLenth = 0 ; hash.put(0 ,-1 ); for (int i = 0 ; i < nums.length; ++i){ sum += nums[i]; if (hash.containsKey(sum)){ maxLenth = Math.max(maxLenth, Math.abs(i - hash.get(sum))); }else { hash.put(sum, i); } } return maxLenth; }
Longest Continuous Increasing Subsequence
求数组的最长连续递增子数组
思路:灰常简单,直接遍历就好
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int findLengthOfLCIS (int [] nums) if (null == nums || nums.length == 0 )return 0 ; int max = 1 ; int curr = 1 ; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] > nums[i-1 ]){ ++curr; max = Math.max(max,curr); }else { curr = 1 ; } } return max; }
Degree of an Array
给一个数组,求最多出现的那个元素的最短连续子数组。
思路:建立一个Node,其中存每个元素第一次出现的位置、最后一次出现的位置、出现次数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Node int idx0; int idxn; int counter; Node(int idx0){ this .idx0 = idx0; counter = 1 ; } } public int findShortestSubArray (int [] nums) if (nums.length <= 1 ) return nums.length; HashMap<Integer,Node> hash = new HashMap<>(); int maxCounter = 1 ; int minLength = Integer.MAX_VALUE; for (int i = 0 ; i < nums.length; ++i){ if (hash.containsKey(nums[i])){ Node curr = hash.get(nums[i]); curr.counter ++; curr.idxn = i; if (curr.counter > maxCounter){ minLength = i - curr.idx0 + 1 ; maxCounter = curr.counter; }else if (curr.counter == maxCounter){ minLength = Math.min(minLength, i - curr.idx0 + 1 ); } }else { Node curr = new Node(i); hash.put(nums[i],curr); } } return minLength == Integer.MAX_VALUE ? 1 : minLength; }
Maximum Product Subarray
求数组的最大子数组积
思路一:(最后一个样例超memory了 )
按照老方法,申请一个数组prod[],其中prod[i]表示[0,i]的乘积。但是[0,i]中可能存在0,因此不太可行。变化一下方式,如果nums[k]==0,那么prod[i] = [k+1,i]的乘积
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 public int maxProduct (int [] nums) if (nums.length == 0 ) return 0 ; if (nums.length == 1 )return nums[0 ]; int [] prod = new int [nums.length]; prod[0 ] = nums[0 ]; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] == 0 ){ prod[i] = 0 ; }else { if (prod[i-1 ] == 0 ){ prod[i] = 1 * nums[i]; }else { prod[i] = prod[i-1 ] * nums[i]; } } } int max = prod[0 ]; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] == 0 ){ max = Math.max(0 ,max); continue ; } max = Math.max(prod[i],max); for (int j = i; j < nums.length; ++j){ if (nums[j] ==0 ){ max = Math.max(0 ,max); break ; } if (nums[i-1 ] == 0 ){ max = Math.max(prod[j],max); }else { max = Math.max(prod[j]/prod[i-1 ], max); } } } return max; }
思路二:动态规划,可以说是相当机智了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 - 用数组positive_max[i]维护原始数组前i个数的子数组乘积中正数的最大值 - 用数组negative_min[i]维护原始数组前i个数的子数组乘积中负数的最小值 状态转移方程为: if A[x] > 0 : positive_max[x] = max(positive_max[x - 1 ] * A[x], A[x]) negative_min[x] = negative_min[x - 1 ] * A[x] else if A[x] < 0 : positive_max[x] = negative_min[x - 1 ] * A[x] negative_min[x] = min(positive_max[x - 1 ] * A[x], A[x]) 代码: public int maxProduct (int [] nums) if (nums.length == 0 ) return 0 ; if (nums.length == 1 )return nums[0 ]; int [] pos_max = new int [nums.length]; int [] neg_min = new int [nums.length]; if (nums[0 ] > 0 ){ pos_max[0 ] = nums[0 ]; }else { neg_min[0 ] = nums[0 ]; } int max = nums[0 ]; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] > 0 ){ pos_max[i] = Math.max(pos_max[i-1 ]*nums[i], nums[i]); neg_min[i] = neg_min[i-1 ] * nums[i]; }else if (nums[i] < 0 ){ pos_max[i] = neg_min[i-1 ] * nums[i]; neg_min[i] = Math.min(pos_max[i-1 ]*nums[i],nums[i]); }else { pos_max[i] = 0 ; neg_min[i] = 0 ; max = Math.max(max, 0 ); } if (pos_max[i] > 0 ){ max = Math.max(max, pos_max[i]); } } return max; } 其实我们可以用更简便的方式,将Pos_max 与 neg_min 压缩: 我们只需要在维护一个局部最大的同时,在维护一个局部最小,这样如果下一个元素遇到负数时,就有可能与这个最小相乘得到当前最大的乘积和,这也是利用乘法的性质得到的。 public int maxProduct (int [] A) if (A==null || A.length==0 ) return 0 ; if (A.length == 1 ) return A[0 ]; int max_local = A[0 ]; int min_local = A[0 ]; int global = A[0 ]; for (int i=1 ;i<A.length;i++) { int max_copy = max_local; max_local = Math.max(Math.max(A[i]*max_local, A[i]), A[i]*min_local); min_local = Math.min(Math.min(A[i]*max_copy, A[i]), A[i]*min_local); global = Math.max(global, max_local); } return global; }
Product of Array Except Self
给一个数。令每个元素等于除了本元素的所有的乘积。求输出。
主要注意:一旦本位为0,就会影响到后面!
思路一:同时考虑一下有几个0.
如果只有1个0,那么只有0位的值为其它元素的乘积。其它位都为0.
如果有大于等于两个0,那每一位都是0.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int [] productExceptSelf(int [] nums) { long allProdcut = 1L ; int zero = 0 ; for (int i = 0 ; i < nums.length; ++i){ if (nums[i] == 0 ){ ++zero; continue ; } allProdcut *= nums[i]; } for (int i = 0 ; i < nums.length; ++i){ if (nums[i] == 0 ){ if (zero == 1 ) nums[i] = (int )allProdcut; }else { if (zero > 0 ) nums[i] = 0 ; else nums[i] = (int ) allProdcut / nums[i]; } } return nums; }
思路二:骚操作
数组的乘积由左边部分的乘积和右边部分的乘积 乘起来得到!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int n = nums.length;int [] res = new int [n];if (n == 0 ) return res;res[0 ] = 1 ; for (int i = 1 ;i < n; ++i){ res[i] = res[i - 1 ] * nums[i - 1 ]; } int r = 1 ;for (int j = n - 2 ; j >= 0 ; --j){ r *= nums[j + 1 ]; res[j] *= r; } return res;
Container With Most Water
给一个非负整数数组,其中元素代表挡板的高度。求某两个挡板,使挡板之间能够乘的水最多。
思路:这道题其实用了一点贪心的思路。
思考公式\(min(a_i,a_j)\times(j-i)\) 。若 a[l] < a[r],只能通过增加二者中较小的a[l]来增加面积,因为j – i已经是目前能达到的最大值了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public int maxArea (int [] height) int max = Integer.MIN_VALUE; int low = 0 , high = height.length - 1 ; while (low < high){ if (height[low] < height[high]){ max = Math.max(max, height[low]*(high - low)); ++low; }else { max = Math.max(max, height[high] * (high - low)); --high; } } return max; }
Array Nesting
给n个点,数组的\(A[i]\) 表示边\((i,A[i])\) 。 问此图最长的环有多长。
思路:一开始没有理清题意。其实这道题很简单哇。哎。
用\(O(n)\) 的时间!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int arrayNesting (int [] nums) if (nums.length <= 1 ) return nums.length; int max = 0 ; for (int i = 0 ; i < nums.length; ++i){ int idx = i; int len = 0 ; while (nums[idx] >= 0 ){ int idx_next = nums[idx]; nums[idx] = -1 ; idx = idx_next; ++len; } max = Math.max(max, len); } return max; }
Find Pivot Index
给一个数组。寻找一个idx,使得它左边的和等于它右边的和。如果不存在,返回-1。
思路:一个个遍历求leftSum和rightSum就好。
注意边界条件。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public int pivotIndex (int [] nums) if (nums.length <= 3 ) return -1 ; int rightSum = 0 ; for (int i = 1 ; i < nums.length; ++i) rightSum += nums[i]; if (rightSum == 0 ) return 0 ; int leftSum = 0 ; for (int i = 0 ; i < nums.length - 1 ; ++i){ leftSum += nums[i]; rightSum -= nums[i+1 ]; if (leftSum == rightSum){ return i+1 ; } } return -1 ; }
# 股票问题
例题9,Best Time to Buy and Sell Time
方案一,动态规划法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 动态规划法。从前向后遍历数组,记录当前出现过的最低价格,作为买入价格,并计算以当天价格出售的收益,作为可能的最大收益,整个遍历过程中,出现过的最大收益就是所求 sell[i] 第i天卖出赚的最多的钱 = price[i] - min 代码: public int maxProfit (int [] prices) int max = 0 ; int min = Integer.MAX_VALUE; for (int i = 0 ; i < prices.length; ++i){ min = Math.min(min, prices[i]); max = Math.max(max, prices[i] - min); } return max; }
股票问题是一系列的问题。我实在是太笨了。现在翻译一下大神的解答好了。
方案二,通用解法
定义如下符号:
prices 长度为nk 代表最大允许的买入次数T[i][k] : 在第i天结束时,通过至多k次交易后,的最大利润。
很容易得出初始化T[-1][k]=T[i][0]=0(没有股票或没有交易时的利润)
同时,第i天都可以——买入、卖出、休息。而且题目要求买入和卖出不可以在同一天进行,且一天最多只可以持有一支股票。那么如果我们在第i天买入,那么这一天之前只能有0只股票。如果我们在第i天卖出,那这一天只能有1只股票。因此我们定义:
T[i][k][0] 为第i天通过至多k次交易后,当天没有股票(保持原样或卖出)的最大利润T[i][k][1] 为第i天通过至多k次交易后,当天有股票(保持原样或买入)的最大利润
因此我们得到了初始化方案:
1 2 T[-1 ][k][0 ] = T[i][0 ][0 ] = 0 ; T[-1 ][k][1 ] = T[i][0 ][1 ] = -Infinity
递推公式:
1 2 T[i][k][0 ] = max(T[i-1 ][k][0 ], T[i-1 ][k][1 ] + prices[i]); T[i][k][1 ] = max(T[i-1 ][k][1 ], T[i-1 ][k-1 ][0 ] - prices[i]);
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public int maxProfit (int [] prices) if (prices.length == 0 ) return 0 ; int [][][] maxProfits = new int [prices.length][2 ][2 ]; maxProfits[0 ][0 ][0 ] = 0 ; maxProfits[0 ][1 ][0 ] = Integer.MIN_VALUE; maxProfits[0 ][1 ][1 ] = -prices[0 ]; maxProfits[0 ][0 ][1 ] = Integer.MIN_VALUE; for (int i = 1 ; i < prices.length; ++i){ maxProfits[i][1 ][0 ] = Math.max(maxProfits[i-1 ][1 ][0 ], maxProfits[i-1 ][1 ][1 ] + prices[i]); maxProfits[i][1 ][1 ] = Math.max(maxProfits[i-1 ][1 ][1 ], maxProfits[i-1 ][0 ][0 ] - prices[i]); } return Math.max(maxProfits[prices.length - 1 ][1 ][0 ],0 ); }
事实上,递推公式的第二个:maxProfits[i][1][1] = Math.max(maxProfits[i-1][1][1], maxProfits[i-1][0][0] - prices[i]);中的maxProfits[i-1][0][0]恒为0。因此我们可以将代码简化为:
1 2 3 4 5 6 7 8 9 10 public int maxProfit (int [] prices) int T_i10 = 0 , T_i11 = Integer.MIN_VALUE; for (int price : prices) { T_i10 = Math.max(T_i10, T_i11 + price); T_i11 = Math.max(T_i11, -price); } return T_i10; }
Best Time to Buy and Sell Stock II
如果可以允许多次买入卖出,但不可以同一天买卖。求最大利润。
方案一,贪婪法
这道题没有交易费的限制,所以我们就无脑贪婪就可以了,见到利润就往上加
哎,明明很简单的题。感觉自己宛如智障。
1 2 3 4 5 6 7 public int maxProfit (int [] prices) int total = 0 ; for (int i = 1 ; i < prices.length; ++i){ if (prices[i] > prices[i-1 ]){total += (prices[i] - prices[i-1 ]);} } return total; }
方案二,通用法
按照上一题的思路,此时k随意了,且递推公式变成了:
1 2 3 4 5 6 7 8 9 10 11 12 13 T[i][k][0 ] = max(T[i-1 ][k][0 ], T[i-1 ][k][1 ] + prices[i]); T[i][k][1 ] = max(T[i-1 ][k][1 ], T[i-1 ][k-1 ][0 ] - prices[i]) = max(T[i-1 ][k][1 ], T[i-1 ][k][0 ] - prices[i]) 因为T[i-1 ][k-1 ][0 ] == T[i-1 ][k][0 ] , 即第i-1 天时如果不持股,那么k-1 次交易与k次交易的最大利润应该是一样的 后期插入:我的理解是,如果这一天允许操作k-1 次或者k次,其实都是一样的,因此多出来的一次没什么用,不足以在一天之内完成。 但这里我不太明白为什么,原作者指出: Sorry for the confusion. So there are two interpretations here. First from a mathematical point of view, limit(k) is the same as limit (k-1 ) when k approaches +infinity. Second, more relevant to this problem, as I said for the case of arbitrary k, when k is sufficiently large, the maximum profits will on longer depend on k but be bound by the number of available stocks. This means if k goes to +infinity, the profits won't change if you increase or decrease the value of k, that is, T[i][k][0] will be the same as T[i][k-1][0] and T[i][k][1] the same as T[i][k-1][1]. Hope this clarifies things a little bit. 坐等张思遥看看吧
代码:
1 2 3 4 5 6 7 8 9 10 public int maxProfit (int [] prices) if (prices.length == 0 ) return 0 ; int T_ik0 = 0 , T_ik1 = Integer.MIN_VALUE; for (int i = 0 ; i < prices.length; ++i){ int T_ik0_old = T_ik0; T_ik0 = Math.max(T_ik0, T_ik1 + prices[i]); T_ik1 = Math.max(T_ik1, T_ik0_old - prices[i]); } return T_ik0; }
Best Time to Buy and Sell Stock with Transaction Fee
接上题,如果买出时有一个手续费。求最大利润。
这道题拿到之后没有思路,就懵了。看了解答才模模糊糊知道了。先把答案记下来吧。哎。难受。
这道题有了交易费,所以当卖出的利润小于交易费的时候,我们就不应该卖了,不然亏了。
通用解法
递推此时有两种写法,要么交易费在买入的时候收取,要么在卖出的时候收取:
1 2 3 4 5 6 7 8 9 10 卖出的时候收取 T[i][k][0 ] = max(T[i-1 ][k][0 ], T[i-1 ][k][1 ] + prices[i] - fee); T[i][k][1 ] = max(T[i-1 ][k][1 ], T[i-1 ][k-1 ][0 ] - prices[i]); 买入的时候收取 T[i][k][0 ] = max(T[i-1 ][k][0 ], T[i-1 ][k][1 ] + prices[i]); T[i][k][1 ] = max(T[i-1 ][k][1 ], T[i-1 ][k-1 ][0 ] - prices[i] - fee); 而 T[i-1 ][k-1 ][0 ] == T[i-1 ][k][0 ]
代码:
1 2 3 4 5 6 7 8 9 10 public int maxProfit (int [] prices, int fee) if (prices.length == 0 ) return 0 ; int T_ik0 = 0 , T_ik1 = Integer.MIN_VALUE; for (int i = 0 ; i < prices.length; ++i){ int T_ik0_old = T_ik0; T_ik0 = Math.max(T_ik0, T_ik1 + prices[i]); T_ik1 = Math.max(T_ik1, T_ik0_old - prices[i] - fee); } return T_ik0; }
带一点贪心的思路
该天结束后手里没有股票。可能是保持前一天的状态,也有可能是今天卖出了。令此时收益为cache
该天结束后手里有股票。可能是保持前一天的状态,也有可能是今天买入了。用hold表示
1 2 3 4 5 6 7 8 9 int maxProfit (vector<int >& prices, int fee) int sold = 0 , hold = -prices[0 ]; for (int price : prices) { int t = sold; sold = max(sold, hold + price - fee); hold = max(hold, t - price); } return sold; }
Best Time to Buy and Sell Stock with Cooldown
假设可以多次买入卖出,但卖出之后必须休息一天才可以继续买入
按照上一题的思路,此时的转移方程为:
1 2 3 4 5 T[i][k][0 ] = max(T[i-1 ][k][0 ], T[i-1 ][k][1 ] + prices[i]); T[i][k][1 ] = max(T[i-1 ][k][1 ], T[i-2 ][k-1 ][0 ] - prices[i]) = max(T[i-1 ][k][1 ], T[i-2 ][k][0 ] - prices[i]); 同时 T[i-2 ][k-1 ][0 ] == T[i-2 ][k][0 ]
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int maxProfit (int [] prices) if (prices.length <= 1 ) return 0 ; int Tlastik_0 = 0 , Tlastik_1 = -prices[0 ], Tik_0 = 0 , Tik_1 = Math.max(Tlastik_1,-prices[1 ]); for (int i = 1 ; i < prices.length; ++i){ int Tik_0_old = Tik_0, Tik_1_old = Tik_1; Tik_0 = Math.max(Tik_0, Tik_1 + prices[i]); Tik_1 = Math.max(Tik_1, Tlastik_0 - prices[i]); Tlastik_0 =Tik_0_old; Tlastik_1 = Tik_1; } return Math.max(Tik_0, Tik_1); }
Best Time to Buy and Sell Stock III
如果允许最多交易两次。那么求最大利润。
按照上一题的思路,此时k <= 2,那么递推公式为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 T[i][k][0 ] = max(T[i-1 ][k][0 ], T[i-1 ][k][1 ] + prices[i]); T[i][k][1 ] = max(T[i-1 ][k][1 ], T[i-1 ][k-1 ][0 ] - prices[i]); 由于 k <= 2 ,因此 if k == 0 T[i][0 ][0 ] = 0 T[i][0 ][1 ] = -Inifity if k == 1 T[i][1 ][0 ] = max(T[i-1 ][1 ][0 ], T[i-1 ][1 ][1 ] + prices[i]); T[i][1 ][1 ] = max(T[i-1 ][1 ][1 ], T[i-1 ][0 ][0 ] - prices[i]); = max(T[i-1 ][1 ][1 ], 0 - prices[i]); if k == 2 T[i][2 ][0 ] = max(T[i-1 ][2 ][0 ], T[i-1 ][2 ][1 ] + prices[i]); T[i][2 ][1 ] = max(T[i-1 ][2 ][1 ], T[i-1 ][1 ][0 ] - prices[i]);
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int maxProfit (int [] prices) if (prices.length == 0 ) return 0 ; int Ti_k0_0 = 0 , Ti_k0_1 = Integer.MIN_VALUE, Ti_k1_0 = 0 , Ti_k1_1 = Integer.MIN_VALUE, Ti_k2_0 = 0 , Ti_k2_1 = Integer.MIN_VALUE; for (int i = 0 ; i < prices.length; ++i){ Ti_k2_0 = Math.max(Ti_k2_0, Ti_k2_1 + prices[i]); Ti_k2_1 = Math.max(Ti_k2_1, Ti_k1_0 - prices[i]); Ti_k1_0 = Math.max(Ti_k1_0, Ti_k1_1 + prices[i]); Ti_k1_1 = Math.max(Ti_k1_1, -prices[i]); } return Math.max(Ti_k2_0, Math.max(Ti_k1_0, Ti_k0_0)); }
当然也有另一种相似的初始化方式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public int maxProfit (int [] prices) if (prices.length == 0 ) return 0 ; int Ti_k0_0 = 0 , Ti_k0_1 = Integer.MIN_VALUE, Ti_k1_0 = 0 , Ti_k1_1 = -prices[0 ], Ti_k2_0 = 0 , Ti_k2_1 = -prices[0 ]; for (int i = 1 ; i < prices.length; ++i){ Ti_k2_0 = Math.max(Ti_k2_0, Ti_k2_1 + prices[i]); Ti_k2_1 = Math.max(Ti_k2_1, Ti_k1_0 - prices[i]); Ti_k1_0 = Math.max(Ti_k1_0, Ti_k1_1 + prices[i]); Ti_k1_1 = Math.max(Ti_k1_1, -prices[i]); } return Math.max(Ti_k2_0, Math.max(Ti_k1_0, Ti_k0_0)); }
Two Sum问题
例题15,Two Sum
给一个数组,求两数之和等于target的idx。
方法一:哈希表
空间\(O(n)\)
如果不要求返回idx,只返回数字呢?
空间\(O(1)\) ,时间\(O(nlogn + n)\)
先排序
两个指针,一头一尾
1 2 3 4 5 6 7 8 9 10 11 12 13 i = 0 ,j = n-1 ; while (i < j){ if (nums[i] + nums[j] > target){ --j; } else if (nums[i] + nums[j] < target){ ++i; }else { return [nums[i],nums[j]] } }
Two Sum II
给一个有序数组,求两数之和等于target的idx。
方法一:hash表
方法二:Two Pointer方法
1 2 3 4 5 6 7 8 9 10 11 12 13 public int [] twoSum(int [] nums, int target) { int i = 0 , j = nums.length - 1 ; while (i < j){ if (nums[i] + nums[j] == target){ return new int []{i + 1 ,j + 1 }; }else if (nums[i] + nums[j] > target){ --j; }else { ++i; } } return null ; }
例题16,Two Sum Closest
求两数之和最接近target,返回两数和与target的差
相似套路
Valid Triangle Number
给一个数组。求数组中能组成三角形的个数。
明明就是two pointer的变种。怎么想都想不出来。哎。我的智商真的有问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int triangleNumber (int [] nums) if (nums.length < 3 ) return 0 ; Arrays.sort(nums); int counter = 0 , n = nums.length; for (int high = n - 1 ; high >= 2 ; --high){ int low = 0 , mid = high - 1 ; while (low < mid){ if (nums[low] + nums[mid] > nums[high]){ counter += mid - low; --mid; }else { ++low; } } } return counter; }
例题17,Three Sum
方法一:hash + 遍历 , 空间\(O(n)\) + 时间\(O(n^2)\)
方法二:排序后two pointer,空间\(O(1)\) + 时间\(O(n^2)\)
排序
求a+b+c = target 固定a , 然后对b + c利用Two Sum方法
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public List<List<Integer>> threeSum(int [] nums){ Arrays.sort(nums); List<List<Integer>> ans = new LinkedList<>(); for (int a = 0 ; a < nums.length; ++a){ if (a > 0 && nums[a] == nums[a - 1 ]) continue ; int i = a + 1 , j = nums.length - 1 ; int target = -nums[a]; int sum; while (i < j){ sum = nums[i] + nums[j]; if (sum == target){ List<Integer> one = new ArrayList<Integer>(3 ); one.add(nums[a]); one.add(nums[i]); one.add(nums[j]); ans.add(one); ++i;--j; while (i < j && nums[i] == nums[i-1 ]){ ++i; } while (i < j && nums[j] == nums[j + 1 ]){ --j; } }else if (sum > target){ --j; }else { ++i; } } } return ans; }
Three Sum Closest
给一个数组和一个target。求三个数之和最接近target的和。
思路:与之前的相似。
排序
求a+b+c = target 固定a , 然后对b + c利用Two Sum方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public int threeSumClosest (int [] nums, int target) Arrays.sort(nums); int sum = 0 ; int minDiff = Integer.MAX_VALUE; for (int a = 0 ; a < nums.length; ++a){ int t = target - nums[a]; int i = a + 1 , j = nums.length - 1 ; int sum2,currDiff; while ( i < j ){ sum2 = nums[i] + nums[j]; currDiff = Math.abs(sum2 - t); if (currDiff < minDiff){ sum = sum2 + nums[a]; minDiff = currDiff; } if (sum2 > t){ --j; }else if (sum2 < t){ ++i; }else { return target; } } } return sum; }
Three Sum Smaller
给一个数组和一个target,求三个数相加小于target的个数。
相似套路。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public int threeSumSmaller (int [] nums, int target) Arrays.sort(nums); int counter = 0 ; int target_curr; for (int a = 0 ; a < nums.length; ++a){ target_curr = target - nums[a]; int i = a + 1 , j = nums.length - 1 ; while (i < j){ if (nums[i] + nums[j] < target_curr){ counter += (j - i); ++i; }else { --j; } } } return counter; }
Four Sum
给一个数组和一个target。求四个数相加等于target的所有可能。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public List<List<Integer>> fourSum(int [] nums, int target) { Arrays.sort(nums); List<List<Integer>> ans = new LinkedList<>(); for (int a = 0 ; a < nums.length; ++a){ if (a > 0 && nums[a] == nums[a - 1 ])continue ; for (int b = a + 1 ; b < nums.length; ++b){ if (b > a + 1 && nums[b] == nums[b-1 ])continue ; int i = b + 1 , j = nums.length - 1 ; while (i < j){ if (nums[a] + nums[b] + nums[i] + nums[j] > target){ --j; }else if (nums[a] + nums[b] + nums[i] + nums[j] < target){ ++i; }else { List<Integer> oneAns = new LinkedList<>(); oneAns.add(nums[a]);oneAns.add(nums[b]); oneAns.add(nums[i]);oneAns.add(nums[j]); ans.add(oneAns); ++i; --j; while (i < j && nums[i] == nums[i - 1 ]){ ++i; } while (i < j && nums[j] == nums[j + 1 ]){ --j; } } } } } return ans; }
Two Pointer问题
Subarray Product Less Than K
给一个正整数数组和一个k。求子数组小于k的个数。
思想:维护一个始终小于k的窗口
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int numSubarrayProductLessThanK (int [] nums, int k) if (nums.length == 0 ) return 0 ; if (nums.length == 1 ) return nums[0 ] > k ? 1 : 0 ; int low = 0 , high = 0 ; long product = 1L ; int counter = 0 ; while (low <= high && high < nums.length){ product *= nums[high]; while (low <= high && product >= k){ product/= nums[low]; ++low; } counter += (high - low + 1 ); ++high; } return counter; }
Longest Substring Without Repeating Characters
给一个字符串。求字符串的最长无重子数组。
思路:两个指针,如果两个指针内没有重复的元素,就把后面的继续后移。如果有重复的,就把前面的移到重复的下一个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public int lengthOfLongestSubstring (String s) if (null == s || s.length() == 0 ) return 0 ; char [] c = s.toCharArray(); int i = 0 , j = 0 ; int max = 0 ; HashMap<Character,Integer> set = new HashMap<>(); while (j < c.length){ if (!set.containsKey(c[j])){ set.put(c[j], j); max = Math.max(j - i + 1 , max); ++j; }else { int repeatIdx = set.get(c[j]); for (int k = i; k <= repeatIdx; ++k){ set.remove(c[k]); } set.put(c[j],j); i = repeatIdx + 1 ; max = Math.max(j - i, max); ++j; } } return max; }
然而上面的这个表现很差。才beats了百分之几。
其实,这个题里面的hashMap的元素不一定必须去除!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public int lengthOfLongestSubstring (String s) if (null == s || s.length() == 0 ) return 0 ; char [] c = s.toCharArray(); int i = 0 , j = 0 ; int max = 0 ; HashMap<Character,Integer> set = new HashMap<>(); while (j < c.length){ if (!set.containsKey(c[j])){ set.put(c[j], j); max = Math.max(j - i + 1 , max); ++j; }else { int repeatIdx = set.get(c[j]); if (repeatIdx >= i){ i = repeatIdx + 1 ; } set.put(c[j],j); max = Math.max(j - i + 1 , max); ++j; } } return max; }
可以改成一个长度为256的数组。骚操作啊骚操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int lengthOfLongtestSubString (String s) char [] str = s.toCharArray(); int l = 0 , r = 0 , max = 0 ; int [] memo = new int [256 ]; Arrays.fill(memo, -1 ); while (r < str.length){ int index = memo[str[r]]; if (index >= l){ l = index + 1 ; }else { max = Math.max(r-l+1 , max); } memo[str[r]] = r; ++r; } return max; }
Implement strStr()
给两个字符串a和b。如果b在a中,返回b的开始idx。
暴力思路:
一个个比较。当然这个思路非常的慢,想哭。只beats了4%。真的伤心。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 private boolean helper (char [] haystack, char [] needle, int h_idx) for (char c : needle){ if (h_idx < haystack.length && c == haystack[h_idx]){ ++h_idx; }else { return false ; } } return true ; } public int strStr (String haystack, String needle) char [] needle_chars = needle.toCharArray(); char [] hays_chars = haystack.toCharArray(); if (needle_chars.length == 0 ) return 0 ; if (hays_chars.length == 0 ) return -1 ; int haystackStart = 0 ; for (int i = 0 ; i < hays_chars.length; ++i){ if (helper(hays_chars, needle_chars, i)) return i; } return -1 ; }
优化
其实。。。。只需要。。。。在大循环的时候,限制i的终止条件就好。。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 private boolean helper (char [] haystack, char [] needle, int h_idx) for (char c : needle){ if (h_idx < haystack.length && c == haystack[h_idx]){ ++h_idx; }else { return false ; } } return true ; } public int strStr (String haystack, String needle) char [] needle_chars = needle.toCharArray(); char [] hays_chars = haystack.toCharArray(); if (needle_chars.length == 0 ) return 0 ; if (hays_chars.length == 0 ) return -1 ; int haystackStart = 0 ; for (int i = 0 ; i <= hays_chars.length - needle_chars.length; ++i){ if (helper(hays_chars, needle_chars, i)) return i; } return -1 ; }
字符串操作
这是最快的操作。真的伤心。
1 return haystack.indexOf(needle);
Reverse String
反转字符串
简单
1 2 3 4 5 6 7 8 9 10 11 public String reverseString (String s) char [] chars = s.toCharArray(); int low = 0 , high = chars.length - 1 ; while (low < high){ char temp = chars[low]; chars[low] = chars[high]; chars[high] = temp; ++low; --high; } return String.valueOf(chars); }
Reverse Vowels of a String
反转字符串中的元音字节
简单的题
元音就是'a','e','i','o','u','A','E','I','O','U'
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public String reverseVowels (String s) HashSet<Character> vowels = new HashSet<>(); char [] v = {'a' ,'e' ,'i' ,'o' ,'u' ,'A' ,'E' ,'I' ,'O' ,'U' }; for (char c : v) vowels.add(c); int low = 0 , high = s.length() - 1 ; char [] s_chars = s.toCharArray(); while (low < high){ while (low < high && !vowels.contains(s_chars[low])) ++low; while (low < high && !vowels.contains(s_chars[high]))--high; if (low < high){ char temp = s_chars[low]; s_chars[low] = s_chars[high]; s_chars[high] = temp; ++low; --high; } } return String.valueOf(s_chars); }
Sum of Square Numbers
给一个数字c。判断c是否是两个数的平方和。
思路:双指针啊我擦
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public boolean judgeSquareSum (int c) if (c < 0 ) return false ; if (c <= 1 ) return true ; int low = 0 , high = (int )Math.sqrt(c); while (low <= high){ if (low*low + high*high == c){ return true ; }else if (low*low + high*high > c){ --high; }else { ++low; } } return false ; }
滑动窗口
Valid Anagram
给两个字符串。判断一个是否是另一个的全排列(字谜)
思路:用两个256的hash表!(其实用一个就行)
1 2 3 4 5 6 7 8 9 10 11 12 13 public boolean isAnagram (String s, String t) if (s.length() != t.length()) return false ; int [] hash = new int [256 ]; for (int i = 0 ; i < s.length(); ++i){ ++hash[s.charAt(i)]; --hash[t.charAt(i)]; } for (int i = 0 ; i < 256 ; ++i){ if (hash[i] != 0 ) return false ; } return true ; }
Group Anagrams
这一题,看了答案,差点被气死,怎么会有如此无理取闹的算法
Find All Anagrams in a String
给两个字符串s和p。求p的全排列出现在's'中的所有起始坐标
思路:按照上一题的滑动窗口的操作!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public List<Integer> findAnagrams (String s, String p) List<Integer> result = new LinkedList<>(); if (s.length() < p.length() || p.length() == 0 ) return result; int [] s_hash = new int [256 ]; int [] p_hash = new int [256 ]; for (int i = 0 ; i < p.length(); ++i){ ++s_hash[s.charAt(i)]; ++p_hash[p.charAt(i)]; } int counter = 0 ; for (int i = 0 ; i < 256 ; ++i){ if (s_hash[i] == p_hash[i]) ++counter; } int low = 0 , high = p.length() - 1 ; while (true ){ if (counter == 256 ){result.add(low);} char low_c = s.charAt(low); if (s_hash[low_c] == p_hash[low_c])--counter; --s_hash[low_c]; if (s_hash[low_c] == p_hash[low_c])++counter; ++low; ++high; if (high >= s.length()) break ; char high_c = s.charAt(high); if (s_hash[high_c] == p_hash[high_c])--counter; ++s_hash[high_c]; if (s_hash[high_c] == p_hash[high_c]) ++counter; } if (counter == 256 ){result.add(low);} return result; }
Permutation in String
判断字符串s2是否包含s1的任意排列的子串
这道题是这一类型的我做的第一道。刚开始的时候想不到滑动窗口,很艰辛。花了一整天时间才消化了。不过之后遇到其它问题的时候还挺顺利的。以后遇到不会的题要使劲总结!加油啊甲乙小朋友!
思路:灰常暴力
给s2一个low和一个high:
初始时,low = 0, high = low
当s2[high] 出现在s1中时,将s1这个位置标记为使用过,将high挪到下一格
如果顺利的话,s1中每个位置都被标记为使用过,那么low --- high之间的字符就是s1的一个排列。
实现的时候过于暴力。借用了hash。当然结果也是非常的慢,大概只beats了2%。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Node int counter; int used; Node(int counter, int used){ this .counter = counter; this .used = used; } } private void clear (HashMap<Character, Node> hash) for (Map.Entry<Character,Node> entry : hash.entrySet()){ entry.getValue().used = 0 ; } } public boolean checkInclusion (String s1, String s2) HashMap<Character, Node> hash = new HashMap<>(); for (char c : s1.toCharArray()){ if (hash.containsKey(c)){hash.get(c).counter += 1 ;} else {hash.put(c,new Node(1 ,0 ));} } int low = 0 , high = 0 ; char [] s2_chars = s2.toCharArray(); int counter = 0 ; while (high < s2_chars.length){ if (hash.containsKey(s2_chars[high])){ Node temp = hash.get(s2_chars[high]); if (temp.used >= temp.counter){ clear(hash); low += 1 ; high = low; counter = 0 ; }else { counter += 1 ; if (counter == s1.length()) return true ; temp.used += 1 ; ++high; } }else { if (counter > 0 ){clear(hash);counter = 0 ;} ++low; high = low; } } return false ; }
优化1,滑动窗口
一共就26个字母,那就为s1和s2各申请一个长度为26的数组。当两个数组完全相等时,即匹配!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public boolean checkInclusion (String s1, String s2) if (s1.length() > s2.length()) return false ; int [] s1map = new int [26 ]; int [] s2map = new int [26 ]; for (int i = 0 ; i < s1.length(); i++) { s1map[s1.charAt(i) - 'a' ]++; s2map[s2.charAt(i) - 'a' ]++; } for (int i = 0 ; i < s2.length() - s1.length(); i++) { if (matches(s1map, s2map)) return true ; s2map[s2.charAt(i + s1.length()) - 'a' ]++; s2map[s2.charAt(i) - 'a' ]--; } return matches(s1map, s2map); } public boolean matches (int [] s1map, int [] s2map) for (int i = 0 ; i < 26 ; i++) { if (s1map[i] != s2map[i]) return false ; } return true ; }
当然,match操作也有优化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public boolean checkInclusion (String s1, String s2) if (s1.length() > s2.length()) return false ; int [] s1map = new int [26 ]; int [] s2map = new int [26 ]; for (int i = 0 ; i < s1.length(); i++) { s1map[s1.charAt(i) - 'a' ]++; s2map[s2.charAt(i) - 'a' ]++; } int count = 0 ; for (int i = 0 ; i < 26 ; i++) if (s1map[i] == s2map[i]) count++; for (int i = 0 ; i < s2.length() - s1.length(); i++) { int r = s2.charAt(i + s1.length()) - 'a' , l = s2.charAt(i) - 'a' ; if (count == 26 ) return true ; s2map[r]++; if (s2map[r] == s1map[r]) count++; else if (s2map[r] == s1map[r] + 1 ) count--; s2map[l]--; if (s2map[l] == s1map[l]) count++; else if (s2map[l] == s1map[l] - 1 ) count--; } return count == 26 ; }
优化2,骚操作
哎。明明知道有优化,就是自己想不出来。
其实不需要找到s1的全排列,因为我们只需要考虑s2中是否包含s1中同样个数的字符,并且这些字符是连在一起的就行了。因此,我们可以使用一个滑动窗口,在s2上滑动。在移动的过程中,先保证窗口内部包含了所有的s1的每个字符。如果当前窗口长度大于s1的长度,那就把窗口左边向右移。
当high往后移动时,即代表将s2[high]加入到窗口中
如果s1中包含s2[high],那么count[s2[high]] > 0,就将计数器cnt--
如果s1中不包含s2[high],那么就将count[s2[high]]--
直到窗口内部的元素恰好全部包含了s1时:
如果窗口大小恰好等于s1,那么就返回true
否则的话,窗口大小一定是大于s1的。那我们就要尝试将窗口变小,也就是将前面的low往后移动
通过上面的操作,如果一个count[s2[low]]==0,那就说明s2[low]一定是出现在s1中的,只是被减去了,而且窗口内部的s2[low]个数恰好等于s1中的个数。为了将low往后移动,那么就要将cnt+1,来弥补这个错误
同时,无论count[s2[low]] 等于几,为了将low向后移动,它都要加一
一定要注意用一个int[256]来对字符进行hash 的操作!!!!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public boolean checkInclusion (String s1, String s2) if (s1.length() > s2.length()) return false ; int [] count = new int [256 ]; for (char c : s1.toCharArray()){ count[c]++; } int len = s1.length(); int cnt = len; char arr[] = s2.toCharArray(); int high = 0 , low = 0 ; while (high < arr.length){ if (count[arr[high]] > 0 ){ cnt--; } count[arr[high]]--; ++high; while (cnt == 0 ){ if (high - low == len){return true ;} if (count[arr[low]] == 0 ){ cnt++; } count[arr[low]]++; low++; } } return false ; }
优化3,骚操作
先看这种解法:
对于每个遍历到的字符,我们在hash表中对于该字符次数减1。一旦该字符次数小于0,那么该字符要么在s1中不曾出现,或者出现的次数超过了s1中的该字符出现次数。那么此时我们就移动窗口的low边界。需要注意的是,每次移动右边界时,hash表对应的字符次数都要+1。如果此时次数不等于0,那么说明该字符不在s1中,继续向右移。直到更新后的次数为0为止。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public boolean checkInclusion (String s1, String s2) if (s1.length() > s2.length()) return false ; int [] count = new int [256 ]; for (char c : s1.toCharArray()){ count[c]++; } int len = s1.length(); char arr[] = s2.toCharArray(); int high = 0 , low = 0 ; while (high < arr.length){ --count[arr[high]]; ++high; if (count[arr[high]] < 0 ){ while (count[arr[low]] != 0 ){ ++low; ++count[arr[low]]; } }else if (high - low + 1 == len) return true ; } return s1.length() == 0 ; }
Minimum Window Substring
给两个字符串,找到一个包含另一个所有元素的最小子串
思路:hash + 双指针!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 private int goHigh (int [] hash_s, int [] hash_t, String s, String t, int high, int same) if (high == s.length() - 1 ) return same; ++high; char s_element = s.charAt(high); if (hash_t[s_element] > hash_s[s_element]) same += 1 ; hash_s[s_element]++; return same; } private int goLow (int [] hash_s, int [] hash_t, String s, String t, int low, int same) char s_element = s.charAt(low); if (hash_t[s_element] > 0 && hash_s[s_element] <= hash_t[s_element]){ same -= 1 ; } hash_s[s_element]--; ++low; return same; } public String minWindow (String s, String t) if (s.length() < t.length() || t.length() == 0 ) return "" ; int [] hash_s = new int [256 ]; int [] hash_t = new int [256 ]; for (int i = 0 ; i < t.length(); ++i){ hash_s[s.charAt(i)]++; hash_t[t.charAt(i)]++; } int same = 0 ; for (int i = 0 ; i < 256 ; ++i){ if (hash_t[i] > 0 && hash_s[i] > 0 ){ same += Math.min(hash_s[i], hash_t[i]); } } int window = Integer.MAX_VALUE; int start = -1 , end = -1 ; int low = 0 , high = t.length() - 1 ; while (low<= s.length() - t.length() && high < s.length()){ if (same == t.length()){ if (high - low + 1 < window){ start = low; end = high; window = high - low + 1 ; } same = goLow(hash_s, hash_t, s, t, low, same); ++low; }else if (same < t.length()){ same = goHigh(hash_s, hash_t, s, t, high, same); ++high; }else { same = goLow(hash_s, hash_t, s, t, high, same); ++low; } } if (start == -1 ) return "" ; return s.substring(start, end + 1 ); }
Gas Station
有n个加油站,每个加油站可以加gas[i] 的油量。从i 到i+1 需要花费cost[i] 的油量。加油站是环形。求一个出发点,能使得它可以走一个环。
一开始就暴解,结果最后一个样例没有通过。
滑动窗口啊!
如果low到high之间的油量不够了,那出发点一定不是low。则low--
如果low到high之间油量大于等于0,那出发点有可能是low。则high++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int canCompleteCircuit (int [] gas, int [] cost) int n = gas.length; int low =0 , high = 0 ; int remain = gas[0 ] - cost[0 ]; int counter = n - 1 ; while (counter > 0 ){ if (remain < 0 ){ --low;low = (low + n)%n; remain += gas[low] - cost[low]; } else { ++high;high %= n; remain += gas[high] - cost[high]; } --counter; } return remain >= 0 ? low : -1 ; }
Contains Duplicate III
给一个数组。求是否存在两个位置,使得|nums[i] - nums[j]| <= t, |i - j| <=k
思路一,排序+滑窗
嗯。建议读者不要采纳这个方法。因为它有点难理解。
由于题目说要|nums[i] - nums[j]| <= t, |i - j| <=k ,因此我第一反应就是滑窗法。
滑窗有两种窗:索引窗或者值窗。
如果用索引窗,即窗口内|i - j| <= k ,那么是不好判断窗口内是否存在nums[i] - nums[j] <= t 的。因此我们换一种思路,用值窗,按照值对数组进行排序,然后维持窗口内nums[i] - nums[j] <= t
按值排序的话,就要保存每个值的索引,因此我建立了一个结点来保存值和索引:
1 2 3 4 5 6 class Node int val; int idx; } Node[] helper = ...
保持窗口内nums[low] - nums[high] <= t 。如果窗口成立,则++high。 否则++low
需要注意的是,如果两个位置的值相等呢?如果我们先得到索引比较大的值,即high 先触碰到索引较大的值。那么:
如果helper[low].idx > helper[high].idx ,那么先输出索引较大的值是比较好的
如果helper[low].idx < helper[high].idx ,那么先输出索引比较大的值的话,就会进行++high操作,然后就会得到索引偏小的值!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Node implements Comparable <Node > long val; int idx; Node(long val, int idx){ this .val = val; this .idx = idx; } @Override public int compareTo (Node o) if (this .val == o.val){ return o.idx - this .idx; } if (this .val - o.val > 0 ) return 1 ; else return -1 ; } } public boolean containsNearbyAlmostDuplicate (int [] nums, int k, int t) Node[] helper = new Node[nums.length]; for (int i = 0 ; i < nums.length; ++i){ helper[i] = new Node(nums[i], i); } Arrays.sort(helper); int low = 0 , high = 1 ; while (high < nums.length){ if (high == low) ++high; else if (helper[high].val - helper[low].val <= t){ if (Math.abs(helper[high].idx - helper[low].idx) <= k) return true ; ++high; }else { ++low; } } return false ; }
思路2,
维持一个长度为k的window, 每次检查新的值是否与原来窗口中的所有值的差值有小于等于t的. 如果用两个for循环会超时O(nk). 使用treeset( backed by binary search tree) 的subSet函数,可以快速搜索. 复杂度为 O(n logk)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public boolean containsNearbyAlmostDuplicate (int [] nums, int k, int t) if (k<1 || t<0 || nums==null || nums.length<2 ) return false ; SortedSet<Long> set = new TreeSet<Long>(); for (int j=0 ; j<nums.length; j++) { SortedSet<Long> subSet = set.subSet((long )nums[j]-t, (long )nums[j]+t+1 ); if (!subSet.isEmpty()) return true ; if (j>=k) { set.remove((long )nums[j-k]); } set.add((long )nums[j]); } return false ; }
Longest Repeating Character Replacement
给一个字符串ABAB ,k表示能换掉的字符个数。求换掉k个之后,最长重复子串的长度。
这题有点难。
滑动窗口:窗口内最多能容纳:“频率最高字符”的个数 + 能替换的个数k
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public int characterReplacement (String s, int k) if (s.length() <= 1 ) return s.length(); int low = 0 ; int [] hash = new int [26 ]; int maxGlb = 0 ; int maxCount = 0 ; for (int high = 0 ; high < s.length(); ++high){ ++hash[s.charAt(high)-'A' ]; maxCount = Math.max(hash[s.charAt(high)-'A' ], maxCount); while (high - low + 1 > maxCount + k){ --hash[s.charAt(low) - 'A' ]; ++low; } maxGlb = Math.max(maxGlb, high - low + 1 ); } return maxGlb; }
数组划分问题
例题18,Partition Array
给一个数组和一个k。移动数组使得小于k的在左边,大于k的在右边。
思路;Two Pointer方法
从左往右找到第一个大于k的
从右往左找到第一个小于k的
交换他俩
例题19,Sort letters by case
字符大小写排序
例题20,Sort Colors
方法1:
先分成0一组,12一组
然后再将12分开
方法2:
参考程序,三分方法
变形:分成三个部分:
x<= low
low< x <= high
x > high
Sort Color II
Interleaving Positive and Negative Numbers
螺旋数组问题
Spiral Matrix
螺旋输出二维数组
要注意边界条件等
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public List<Integer> spiralOrder (int [][] matrix) if (matrix.length == 0 || matrix[0 ].length == 0 ) return new ArrayList<>(0 ); List<Integer> res = new ArrayList<>(matrix.length * matrix[0 ].length); int left = 0 , right = matrix[0 ].length - 1 , top = 0 , bottom = matrix.length - 1 ; int i = 0 ,j = 0 ; while (bottom >= top && left <= right) { j = left; while (left <= right && j <= right) { res.add(matrix[top][j]); ++j; } top++; i = top; while (bottom >= top && i <= bottom) { res.add(matrix[i][right]); ++i; } right--; j = right; while (bottom >= top && j >= left) { res.add(matrix[bottom][j]); --j; } bottom--; i = bottom; while (left <= right && i >= top) { res.add(matrix[i][left]); --i; } left++; } return res; }
Spiral Matrix II
输出\(n\times n\) 的螺旋数组(元素从1开始依次递增)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public int [][] generateMatrix(int n) { int [][] matrix = new int [n][n]; int i = 0 ,j = 0 ; int val = 1 ; int left = 0 , right = n - 1 , top = 0 , bottom = n - 1 ; while (left <= right && top <= bottom){ j = left; while (left <= right && j <= right){ matrix[top][j++] = val++; } i = ++top; while (top <= bottom && i <= bottom){ matrix[i++][right] = val++; } j = --right; while (left <= right && j >= left){ matrix[bottom][j--] = val++; } i = --bottom; while (top <= bottom && i >= top){ matrix[i--][left] = val++; } ++left; } return matrix; }
区间问题
Merge Intervals
给一些区间。输出区间的合并结果。
要点:
List 的Collections.sort()排序
Comparator的用法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class CompareInterval implements Comparator <Interval > @Override public int compare (Interval o1, Interval o2) return o1.start - o2.start; } } public List<Interval> merge (List<Interval> intervals) if (intervals.size() == 0 ) return intervals; Collections.sort(intervals, new CompareInterval()); int start = intervals.get(0 ).start, end = intervals.get(0 ).end; List<Interval> result = new LinkedList<>(); for (Interval interval : intervals){ if (interval.start <= end){ end = Math.max(end,interval.end); }else { result.add(new Interval(start,end)); start = interval.start; end = interval.end; } } if (intervals.size() > 0 ){result.add(new Interval(start,end));} return result; }
Insert Interval
给一些区间。将另一个区间与这些区间合并。
要点:细心!边界条件!!!!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public List<Interval> insert (List<Interval> intervals, Interval newInterval) List<Interval> result = new LinkedList<>(); boolean begin = false ; Interval last = newInterval; for (Interval interval : intervals){ if (!begin) { if (interval.end >= newInterval.start && interval.start <= newInterval.end) { interval.end = Math.max(interval.end, newInterval.end); interval.start = Math.min(interval.start, newInterval.start); last = interval; begin = true ; } else if (interval.start > newInterval.end){ result.add(newInterval); begin = true ; } result.add(interval); }else { if (interval.start <= last.end){ last.end = Math.max(interval.end, last.end); }else { result.add(interval); } } } if (!begin){ result.add(newInterval); } return result; }
Summary Ranges
给一个无重数组,如果相邻两个数字差为1,则这两个数在一个区间。输出数组的所有区间。
这道题还好。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public List<String> summaryRanges (int [] nums) List<String> result = new LinkedList<>(); if (nums.length == 0 )return result; int start = nums[0 ]; int end = nums[0 ]; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] == nums[i - 1 ] + 1 ){ end = nums[i]; }else { if (start == end){ result.add(String.valueOf(start)); }else { result.add(String.valueOf(start)+"->" +String.valueOf(end)); } start = nums[i]; end = nums[i]; } } if (start == end){ result.add(String.valueOf(start)); }else { result.add(String.valueOf(start)+"->" +String.valueOf(end)); } return result; }
Non-overlapping Intervals
给一些区间[ [1,2], [2,3], [3,4], [1,3] ], 如果想让区间无重复区域,那么最少拿掉多少个区间才可以?
先排序,并维持当前无重区间的最后一个end
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Comparator<Interval> comparator = new Comparator<Interval>() { @Override public int compare (Interval o1, Interval o2) return o1.start - o2.start; } }; public int eraseOverlapIntervals (Interval[] intervals) if (intervals.length == 0 ) return 0 ; Arrays.sort(intervals,comparator); int eraseNum = 0 ; int lastEnd = intervals[0 ].end; for (int i = 1 ; i < intervals.length; ++i){ if (intervals[i].start < lastEnd){ ++eraseNum; if (intervals[i].end >= lastEnd) { continue ; } } lastEnd = intervals[i].end; } return eraseNum; }
Minimum Number of Arrows to Burst Balloons
给一个二维数组[[10,16], [2,8], [1,6], [7,12]] ,每个元素代表一个气球的start和end。问至少多少箭可以把这些气球扎破。
思路差不多
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Comparator<int []> comparator = new Comparator<int []>() { @Override public int compare (int [] o1, int [] o2) return o1[0 ] - o2[0 ]; } }; public int findMinArrowShots (int [][] points) if (points.length == 0 ) return 0 ; Arrays.sort(points, comparator); int arrows = 1 ; int lastEnd = points[0 ][1 ]; for (int i = 1 ; i < points.length; ++i){ if (points[i][0 ] <= lastEnd){ lastEnd = Math.min(lastEnd, points[i][1 ]); }else { ++arrows; lastEnd = points[i][1 ]; } } return arrows; }
My Calendar I
设计一个Calendar类,每次进行book(start, end)操作。如果这次时间与之前的行程冲突,那么返回false。否则保存新的行程,并返回true。
思路:想着用树来表示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 节点: 区间,由start和end表示 左孩子:所有在start之前的行程 右孩子:所有在end之后的行程 代码: class MyCalendar class Node int start; int end; Node left; Node right; Node(int start, int end){ this .start = start; this .end = end; } } Node root; public MyCalendar () public boolean book (int start, int end) if (null == root){ root = new Node(start,end); return true ; }else { Node curr = root; Node parent = root; int ifLeft = 0 ; while (null != curr){ parent = curr; if (end <= curr.start){ curr = curr.left; ifLeft = 1 ; }else if (start >= curr.end){ curr = curr.right; ifLeft = -1 ; }else { return false ; } } if (ifLeft == 1 ){ parent.left = new Node(start,end); return true ; }else if (ifLeft == -1 ){ parent.right = new Node(start,end); return true ; } } return false ; } }
My Calendar II
follow up。如果允许最多有2个行程冲突呢?
这道题自己没写上。想复杂了。
方法一
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 List<int []> books; List<int []> overlaps; public MyCalendarTwo () books = new ArrayList<>(); overlaps = new ArrayList<>(); } public boolean book (int start, int end) for (int [] overlaps : overlaps){ if (Math.max(overlaps[0 ], start) < Math.max(overlaps[1 ], end)){ return false ; } } for (int [] book : books){ int overLapStart = Math.max(book[0 ], start); int overLapEnd = Math.min(book[1 ], end); if (overLapStart < overLapEnd){ overlaps.add(new int []{overLapStart, overLapEnd}); } } books.add(new int []{start, end}); return true ; }
其它数组操作
Minimum Moves to Equal Array Elements
给一个数组。规定每轮迭代为:选择n-1个元素加一。求问当经过多少轮迭代后,数组中每个元素都相同?
一开始暴解,超时了。看了答案才知道要用数学方式计算一下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 定义 sum = 初始数组的和 minNum = 初始数组最小值 通过m次操作后,得到的数组元素都是x,因此 sum + m*(n-1 ) = x*n 而且 x = minNum + m 那么 m = sum - minNum*n public int minMoves (int [] nums) { int sum = 0 ; int minNum = Integer.MAX_VALUE; for (int i = 0 ; i < nums.length; ++i){ sum += nums[i]; minNum = Math.min(minNum, nums[i]); } return sum - minNum*nums.length; }
给一个数组。规定每轮迭代为:选择1个元素加减一。求问当经过多少轮迭代后,数组中每个元素都相同?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public int minMoves2 (int [] nums) if (nums.length == 0 ) return 0 ; int sum = 0 ; Arrays.sort(nums); int mid = nums[nums.length / 2 ]; for (int i = 0 ; i < nums.length; ++i){ sum += Math.abs(nums[i] - mid); } return sum; }
Game of Life
给一个二维数组,1代表本轮活着,0代表本轮死了。如果:
如果某点的活着的邻居少于两个,则它死亡
如果某点有2/3个活着的邻居,则它可以进入下一代
如果某点有3个以上活着的邻居,则它死亡
如果某死点周围只有三个活着的邻居,则它复活
思路:为了在原地进行替换,我们定义:
1 2 3 4 5 6 令下一时刻: * 1 = 下一轮活(本轮活) * 2 = 下一轮死(本轮是活的) * * -1 = 复活(本轮是死的) * -2 = 下一轮死(本轮死)
因此:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 private int getBoardVal (int [][] board, int i, int j) if (i < 0 || i >= board.length || j < 0 || j >= board[0 ].length ){ return 0 ; } if (board[i][j] <= 0 ) return 0 ; else return 1 ; } private int getLiveNeighbors (int [][] board, int i, int j) int live = 0 ; for (int q = -1 ; q < 2 ; ++q) { live += getBoardVal(board, i - 1 , j + q); live += getBoardVal(board, i + 1 , j + q); } live += getBoardVal(board, i, j + 1 ); live += getBoardVal(board, i, j - 1 ); return live; } public void gameOfLife (int [][] board) if (board.length == 0 || board[0 ].length == 0 )return ; for (int i = 0 ; i < board.length; ++i){ for (int j = 0 ; j < board[0 ].length; ++j){ if (board[i][j] <= 0 ){ if (getLiveNeighbors(board,i,j) == 3 ){ board[i][j] = -1 ; } }else { int liveNeibor = getLiveNeighbors(board,i,j); if (liveNeibor < 2 || liveNeibor > 3 ){ board[i][j] = 2 ; }else { } } } } for (int i = 0 ; i < board.length; ++i){ for (int j = 0 ; j < board[0 ].length; ++j){ if (board[i][j] == 1 || board[i][j] == -1 ){ board[i][j] = 1 ; }else { board[i][j] = 0 ; } } } }
Beautiful Arrangement II
给一个n和一个k。求一个长度为n的数组,要求数组的\(a_{i+1}-a_i\) 至少有k个不同的数。
思路:找到规律,直接生成即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int [] constructArray(int n, int k) { int [] nums = new int [n]; int max = k + 1 , min = 1 ; int filled = 0 ; while (filled < n ){ if (max > min){ nums[filled] = min; ++filled; nums[filled] = max; ++filled; --max; ++min; }else if (max == min){ nums[filled] = max; ++filled; --max;++min; }else { nums[filled] = filled + 1 ; ++filled; } } return nums; }
1-bit and 2-bit Characters
给一个数组,元素由1或0.其中0代表一个东西,10 or 11 代表另一个东西。求这个数组是否可以以0结尾。
思路:碰到1就跳两格,碰到0就只能跳一格。
1 2 3 4 5 6 7 8 9 10 11 12 private boolean helper (int [] bits, int idx) if (idx >= bits.length) return false ; if (idx == bits.length - 1 ) return bits[idx] == 0 ; if (bits[idx] == 1 ){ return helper(bits, idx + 2 ); }else { return helper(bits, idx + 1 ); } } public boolean isOneBitCharacter (int [] bits) return helper(bits,0 ); }
Multiply Strings
计算字符串的大数乘法
我的思路:按照竖式计算乘法的方式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 public String multiply (String num1, String num2) if ((num1.length() == 0 || num2.length() == 0 )|| (num1.length() == 1 && num1.equals("0" ))|| (num2.length() == 1 && num2.equals("0" ))) return "0" ; if (num1.length() > num2.length()){ String temp = num1; num1 = num2; num2 = temp; } int [] nums1 = new int [num1.length()], nums2 = new int [num2.length()]; for (int i = 0 ; i < num1.length(); ++i) nums1[i] = num1.charAt(i) - '0' ; for (int i = 0 ; i < num2.length(); ++i) nums2[i] = num2.charAt(i) - '0' ; int n1 = num1.length(), n2 = num2.length(); int [][] temp = new int [n1][n2]; for (int i = n1 - 1 ; i >= 0 ; --i){ for (int j = 0 ; j < n2; ++j){ temp[i][j] = nums1[n1 - i - 1 ] * nums2[n2 - j - 1 ]; } } StringBuilder sb = new StringBuilder(); int j = 0 ; int last = 0 ; while (true ){ int sum = 0 ; boolean finsh = true ; for (int line = 0 ; line < n1; ++line){ if (j - line >= 0 && j - line < n2){ sum += temp[line][j - line]; finsh = false ; } if (j - line < 0 ) break ; } if (finsh) break ; sum += last; last = sum / 10 ; sum = sum % 10 ; sb.append(sum); ++j; } if (last > 0 )sb.append(last); return sb.reverse().toString(); }
自己吭哧吭哧写半天,还是人家写的好。。。。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public String multiply (String nums1, String nums2) int m = num1.length(), n = num2.length(); int [] pos = new int [m + n]; for (int i = m - 1 ; i >= 0 ; --i){ for (int j = n - 1 ; j >= 0 ; --j){ int mul = (num1.charAt(i) - '0' ) * (num2.charAt(j) - '0' ); int p1 = i + j, p2 = p1 + 1 ; mol += pos(p2); pos[p1] += sum/10 ; pos[p2] = sum%10 ; } } StringBuilder sb = new StringBuilder(); for (int p : pos)if (!(sb.length() == 0 && p = 0 )) sb.append(p); return sb.length() == 0 ? "0" : sb.toString(); }
H-Index
给一个数组,代表一个作者的各论文引用次数。求h。其中h代表这个作者有h篇文章的引用次数至少为h。
思路1, 排序,\(O(nlogn)\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int hIndex (int [] citations) if (citations.length == 0 ) return citations.length; if (citations.length == 1 ){ if (citations[0 ] == 0 ) return 0 ; else return 1 ; } Arrays.sort(citations); if (citations[citations.length - 1 ] == 0 ) return 0 ; int h = citations.length; for (int i = citations.length - 1 ; i > 0 ; --i){ if (citations[i-1 ] <= citations.length - i){ h = citations.length - i; break ; } } return h; }
思路2,桶排序
因为h绝对不会大于n,因此我们可以将所有大于n的引用全部认为是n。这样就可以统计引用次数为0-n的论文的个数。
Buckets
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int hIndex (int [] citations) int n = citations.length; int [] buckets = new int [n+1 ]; for (int c : citations) { if (c >= n) { buckets[n]++; } else { buckets[c]++; } } int count = 0 ; for (int i = n; i >= 0 ; i--) { count += buckets[i]; if (count >= i) { return i; } } return 0 ; }
H-Index II
如果输入数组已排序呢?
思路1:上题思路1
思路2,二分法
骚操作啊骚操作
1 2 3 4 5 6 7 8 9 10 11 12 public int hIndex (int [] citations) if (citations == null || citations.length == 0 ) return 0 ; int l = 0 , r = citations.length; int n = citations.length; while (l < r){ int mid = l + (r - l) / 2 ; if (citations[mid] == n - mid) return n - mid; if (citations[mid] < citations.length - mid) l = mid + 1 ; else r = mid; } return n - l; }
Max Chunks To Make Sorted
给一个数组,[1,0,2,3,4]。 我们想把数组拆成几块,例如拆成[1,0],[2,3,4],每块分别排序后再将块按照原顺序拼起来使得总体有序。请问我们最多可以拆成多少块?
这道题我想了很久,最后还是用的递归解答。思路有点复杂。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 Boolean[][] memo; private boolean check (int [] arr, int start, int end) if (memo[start][end] != null ) return memo[start][end]; boolean flag = true ; for (int i = start; i <= end; ++i){ if (arr[i] >= start && arr[i] <= end){ memo[start][i] = true ; }else { flag = false ; break ; } } memo[start][end] = flag; return flag; } private int helper (int [] arr, int start) if (start >= arr.length) return 0 ; if (arr[start] == start) return 1 + helper(arr, start + 1 ); for (int end = start + 1 ; end < arr.length; ++end){ if (check(arr,start, end)) return 1 + helper(arr, end + 1 ); } return 0 ; } public int maxChunksToSorted (int [] arr) memo = new Boolean[arr.length][arr.length]; for (int i = 0 ; i < memo.length; ++i){ if (arr[i] == i) {memo[i][i] = true ;} else {memo[i][i] = false ;} Arrays.fill(memo[i], null ); } return helper(arr, 0 ); }
看看人家O(N)的解法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public int maxChunksToSorted (int [] arr) int n = arr.length; int [] maxOfLeft = new int [n]; int [] minOfRight = new int [n]; maxOfLeft[0 ] = arr[0 ]; for (int i = 1 ; i < n; i++) { maxOfLeft[i] = Math.max(maxOfLeft[i-1 ], arr[i]); } minOfRight[n - 1 ] = arr[n - 1 ]; for (int i = n - 2 ; i >= 0 ; i--) { minOfRight[i] = Math.min(minOfRight[i + 1 ], arr[i]); } int res = 0 ; for (int i = 0 ; i < n - 1 ; i++) { if (maxOfLeft[i] <= minOfRight[i + 1 ]) res++; } return res + 1 ; }
还有升级版:
只用求最大值就可以了,因为序列的内容唯一且连续,所以若arr[i]为最大值且 i == arr[i],则说明,小于 i的部分已经可以且一定顺序连续地排序
For example,
1 2 3 4 5 original: 0, 2, 1, 4, 3, 5, 7, 6 max: 0, 2, 2, 4, 4, 5, 7, 7 sorted: 0, 1, 2, 3, 4, 5, 6, 7 index: 0, 1, 2, 3, 4, 5, 6, 7
The chunks are: 0 | 2, 1 | 4, 3 | 5 | 7, 6
1 2 3 4 5 6 7 8 9 10 11 12 13 public int maxChunksToSorted (int [] arr) if (arr == null || arr.length == 0 ) return 0 ; int count = 0 , max = 0 ; for (int i = 0 ; i < arr.length; i++) { max = Math.max(max, arr[i]); if (max == i) { count++; } } return count; }
Increasing Triplet Subsequence
判断给定数组里是否存在长度为3的递增子序列(可以不连续)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public boolean increasingTriplet (int [] nums) if (nums.length < 3 )return false ; int min1 = nums[0 ]; int min2 = Integer.MAX_VALUE; for (int i = 1 ; i < nums.length; ++i){ if (nums[i] <= min1){ min1 = nums[i]; }else if (nums[i] <= min2){ min2 = nums[i]; }else { return true ; } } return false ; }
Rotate Function
给一个数组A。其中B是A向右移动k次得到的数组。定义F(k) = 0 * Bk[0] + 1 * Bk[1] + ... + (n-1) * Bk[n-1] 。求最大的f(k), k = 0,1,...,A.length - 1
思路:f[k] = f[k-1] + sum - n*A[n-k]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public int maxRotateFunction (int [] A) int n = A.length; int sum = 0 ; int fk = 0 ; for (int i = 0 ; i < n; ++i){ fk += i*A[i]; sum += A[i]; } int max = fk; for (int k = 1 ; k < n; ++k){ fk += sum; fk -= n*A[n - k]; max = Math.max(fk, max); } return max; }
Battleships in a Board
给一个board[][] ,其中元素由X 或者. 。X 代表船舰,. 代表空。我们规定同一个船舰可以占多个格子,但是必须是一个竖条或者一个横列。而且规定船舰不许相邻或者相交。要求用o(n) 的时间复杂度,\(o(1)\) 的空间复杂度求出有几个船舰。
思路:既然船舰不可以相交或者相邻,那么船舰只有三种可能:横着的船舰,竖着的船舰和孤立的船舰。
横着的船舰:除了最左端点外,每一点都有左相邻的X
竖着的船舰:除了最上端点外,每一天都有上相邻的X
孤立的船舰,没有相邻的X
那么当我们遇到一个X时,就++count。然后需要去除重复计算的部分。我们可以:
如果遇到一个有右X的X,那么就不要++
如果遇到一个有上X的X,那么就不要++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int countBattleships (char [][] board) int count = 0 ; for (int row = 0 ; row < board.length; ++row){ for (int col = 0 ; col < board[row].length; ++col){ if (board[row][col] == 'X' ) { if (col > 0 && board[row][col-1 ] == 'X' ){ continue ; }else if (row > 0 && board[row - 1 ][col] == 'X' ){ continue ; } ++count; } } } return count; }
Reconstruct Original Digits from English
给一个字符串,表示0~9 的数字的英文的乱序。例如"owoztneoer" 代表012。给一个字符串,求出对应的数字串(从小到大输出)
原理:
1 2 "zero" ,"one" ,"two" ,"three" ,"four" ,"five" ,"six" , "seven" ,"eight" ,"nine" 0 1 2 3 4 5 6 7 8 9
起初
z一定是0
w一定是2
u一定是4
x一定是6
s一定是7
将上面这些去除后,剩下了one three five eight nine,此刻
只剩下了eight和nine
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 int [] hash = null ;String[] keys = {"zero" ,"one" ,"two" ,"three" ,"four" , "five" ,"six" , "seven" ,"eight" ,"nine" }; private void haha (int [] nums, int [] temp, char [] temp_char) for (int k = 0 ; k < temp.length; ++k){ nums[temp[k]] = hash[temp_char[k] - 'a' ]; if (nums[temp[k]] <= 0 ) continue ; for (char c : keys[temp[k]].toCharArray()){ hash[c-'a' ] -= nums[temp[k]]; } } } private String helper () int [] nums = new int [10 ]; int [] temp = {0 ,2 ,4 ,6 ,7 }; char [] temp_char = {'z' ,'w' ,'u' ,'x' ,'s' }; haha(nums, temp, temp_char); temp = new int []{1 ,5 ,3 }; temp_char = new char []{'o' ,'f' ,'r' }; haha(nums, temp, temp_char); temp = new int []{8 ,9 }; temp_char = new char []{'t' ,'i' }; haha(nums, temp, temp_char); StringBuilder sb = new StringBuilder(); for (int number = 0 ; number < 10 ; ++number){ while (nums[number] > 0 ){ sb.append(number); --nums[number]; } } return sb.toString(); } public String originalDigits (String s) hash = toHash(s); return helper(); } public int [] toHash(String s){ int [] hashed = new int [26 ]; for (char c: s.toCharArray()){ ++hashed[c-'a' ]; } return hashed; }
加减乘除问题
Pow(x, n)
实现\(x^n\) 操作
二分法:$2{10}={2 2}^{5} $
第一次写出来的递归,结果爆栈了,现在改成非递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public double helper (double x, int n) double result = x; double another = 1 ; while (true ){ if (n%2 == 1 ) another = another*result; result = result * result; n = n / 2 ; if (n == 1 )break ; if (result == Double.POSITIVE_INFINITY){ return result; } } return result*another; } public double myPow (double x, int n) if (n == 0 ) return 1 ; if (n == 1 ) return x; if (n == -1 ) return 1 /x; if (x == 1 ) return 1 ; if (x == -1 ){ if (n%2 == 0 ) return 1 ; else return -1 ; } if (n < 0 ) return 1 /helper(x,-n); return helper(x,n); }
Largest Number
给一个数组,用元素组成一个最大的整数
哎。调了好久。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 int intDigit (int val) int counter = 0 ; while (val > 0 ){ ++counter; val /= 10 ; } return counter; } Comparator<Integer> cmp = new Comparator<Integer>() { @Override public int compare (Integer o1, Integer o2) if (o1 == 0 || o2 == 0 ) return o2.compareTo(o1); if (o1.equals(o2)) return 0 ; int o1Digit = intDigit(o1); int o2Digit = intDigit(o2); double candidate1 = o1 * (double )Math.pow(10 , o2Digit) + o2; double candidate2 = o2 * (double )Math.pow(10 , o1Digit) + o1; if (candidate1 > candidate2){ return -1 ; }else return 1 ; } }; public String largestNumber (int [] nums) if (nums.length == 0 ) return "0" ; Integer[] numsCopy = new Integer[nums.length]; for (int i = 0 ; i < nums.length; ++i){numsCopy[i] = nums[i];} Arrays.sort(numsCopy,cmp); if (numsCopy[0 ] == 0 ) return "0" ; StringBuilder sb = new StringBuilder(); for (Integer e : numsCopy){ sb.append(e); } return sb.toString(); }
Power of Three
给一个数,判断它是否是3的次方。
方法一,循环
1 2 3 4 5 6 public boolean isPowerOfThree (int n) if (n > 1 ){ while (n%3 == 0 ) n /= 3 ; } return n == 1 ; }
方法二,骚操作
1 2 3 4 5 6 int const Max3PowerInt = 1162261467 ; int const MaxInt32 = 2147483647 ; bool isPowerOfThree (int n) { if (n <= 0 || n > Max3PowerInt) return false ; return Max3PowerInt % n == 0 ; }
Power of Four
给一个数,判断它是否是4的次方。
方法一,循环
1 2 3 4 5 6 7 public boolean isPowerOfFour (int num) if (num < 1 ) return false ; while (num % 4 == 0 ){ num /= 4 ; } return num == 1 ; }
方法二,骚操作
这次不能使用上面的方法,因为4不是质数。
1 2 3 4 5 public boolean isPowerOfFour (int num) return num > 0 && (num&(num-1 )) == 0 && (num & 0x55555555 ) != 0 ; }
参考资料
Most consistent ways of dealing with the series of stock problems 【刷题总结】买卖股票最大利润问题