甲乙小朋友的房子

甲乙小朋友很笨，但甲乙小朋友不会放弃

0%

算法-回溯法

发表于 更新于 分类于

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

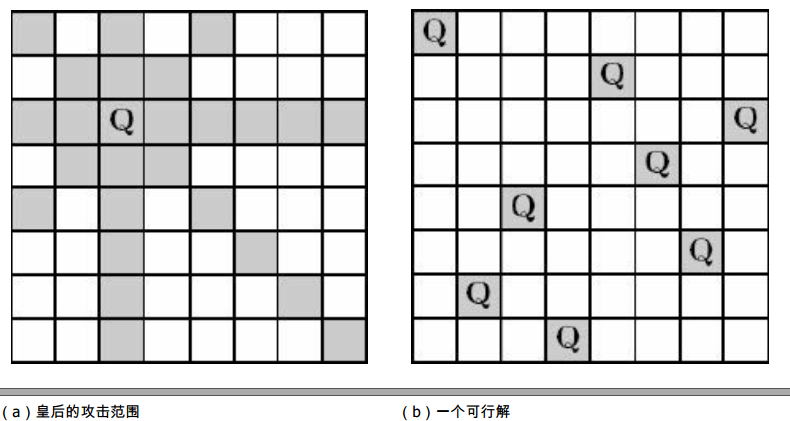
八皇后问题

在棋盘上放置8个皇后，使得它们互不攻击，此时每个皇后的攻击范围为同行同列和同 对角线，要求找出所有解，如图7-4所示。

暴力思路：

64选8，有\(C_{64}^8\)种方案。

优化：

因为恰好每行每列各放置一个皇后，那就是一个全排列问题。而0~7的排列一共只有\(8! = 40320\)个。如果枚举的话，也没多少个。

为了方便分析，我们先把问题简化为4皇后问题。

假如皇后现在的位置是（0,2.*,*)

即：

1
2
3
4
1 * * *
* * 1 *
* * * *
* * * *

此时后面两个皇后无论放哪里，都会和前两行的皇后冲突。此时，递归函数将不再递归调用它自身，而是返回上一层。这个就叫回溯。

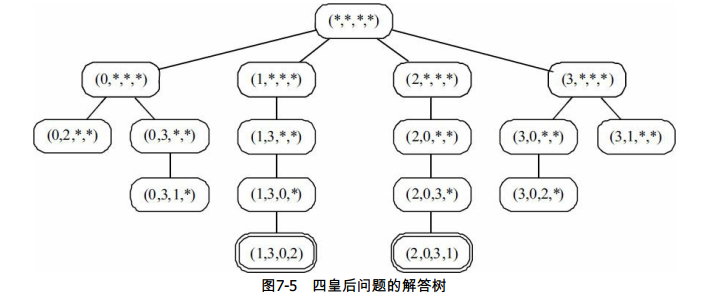
我们画出四皇后的解答树（每个元素代表第i个皇后放在第j列）：

因此，八皇后问题可以这么写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int counter = 0;
int[] C = new int[8]; // C[i]表示第i行的皇后放在了C[i]列
void search(int cur){
  if(cur == n){ // n个皇后都不冲突
    ++counter;
    return;
  }
  for(int i = 0; i < n; ++i){
    int ok = 1;
    // 尝试把第cur行的皇后放在第i列
    C[cur] = i;
    // 检查是否和前面皇后冲突
    for(int j = 0; j < cur; ++j){
      if(C[cur] == C[j]||
        cur - C[cur] == j - C[j]||
         CUR + C[cur] == j + C[j]){
        ok = 0;
        break; // 如果冲突，就不再继续搜索
      }
      if(ok) search(cur + 1);
    }
  }
}

进一步优化：

骚操作：用二维数组vis[3][]判断当前尝试的皇后是否与其他皇后冲突。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
先看看这个：

  0 1 2 3
0 1 * * *
1 * 1 * *
2 * * 1 *
3 * * * 1

我们看看标1的对角线上的i和j有什么关系：

这个对角线i == j

我们看下一个对角线：


  0 1 2 3
0 * 1 * *
1 * * 1 *
2 * * * 1
3 * * * *

这个对角线 i == j + 1
  
其实，这个方向的对角线，只要在一个对角线上，那么 i - j 就是一个定值

那么：

vis[0][i] :第i列是否已有皇后；
vis[1][j + i] : 第j行i列对应的对角线是否已经有皇后（因为同一个对角线上的i + j都是相等的）
vis[2][j - i + n] ： 第j行i列对角线是否已经有皇后 (同一对角线上 j - i 是一个定值 ， 但可能出现负数，因此加一个n)
  
boolean[][] vis ;
void search(int cur){
  if(cur == n){ // n个皇后都不冲突
    ++counter;
    return;
  }
  for(int i = 0; i < n; ++i){
    // 尝试把第cur行的皇后放在第i列
    C[cur] = i;
    // 检查是否和前面皇后冲突
    if(!vis[0][i] && !vis[1][cur + i] && !vis[2][cur - i + n]){
      C[cur] = i;
      vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = true;
      search(cur + 1);
      vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = false;
    }
  }
}

N-Queens

N皇后问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
List<List<String>> result = new LinkedList<>();
    boolean[][] vis ;
    /**
     * vis[0][i] : 第i列有没有皇后
     * vis[1][i + j] : 第 i+j 对角线有无皇后
     * vis[2][i - j + n] : 第 i-j 对角线有无皇后**/
    private void helper(int row, List<String> pos, int n){
        if(row == n){
            List<String> one = new LinkedList<>();
            one.addAll(pos);
            result.add(one);
            return;
        }
        // 尝试将第row行的皇后放入第col列
        for(int col = 0; col < n; ++ col){
            if(!vis[0][col] && !vis[1][col + row] && !vis[2][col - row + n]){
                // 构建第row行的皇后阵列
                StringBuilder strBu = new StringBuilder();
                int i = 0;
                while (i < n){
                    if(i == col) {
                        strBu.append("Q");
                    }else{
                        strBu.append(".");
                    }
                    ++i;
                }
                pos.add(strBu.toString());
                vis[0][col] = true;
                vis[1][col + row] = true;
                vis[2][col - row + n] = true;
                helper(row + 1, pos, n);
                pos.remove(pos.size() - 1);
                vis[0][col] = false;
                vis[1][col + row] = false;
                vis[2][col - row + n] = false;
            }
        }
    }
    public List<List<String>> solveNQueens(int n) {
        vis = new boolean[3][2*n];
        helper(0,new LinkedList<>(), n);
        return result;
    }

N-Queens II

求N皇后的所有的可能排列数目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
boolean[][] vis ;
    /**
     * vis[0][i] : 第i列有没有皇后
     * vis[1][i + j] : 第 i+j 对角线有无皇后
     * vis[2][i - j + n] : 第 i-j 对角线有无皇后**/
    private int helper(int row, int n){
        if(row == n){
            return 1;
        }
        int counter = 0;
        // 尝试将第row行的皇后放入第col列
        for(int col = 0; col < n; ++ col){
            if(!vis[0][col] && !vis[1][col + row] && !vis[2][col - row + n]){
                vis[0][col] = true;
                vis[1][col + row] = true;
                vis[2][col - row + n] = true;
                counter += helper(row + 1, n);
                vis[0][col] = false;
                vis[1][col + row] = false;
                vis[2][col - row + n] = false;
            }
        }
        return counter;
    }
    public int totalNQueens(int n) {
        vis = new boolean[3][2*n];
        return helper(0, n);
    }

全排列问题

全排列问题主要有以下几个知识点：

  • 暴力枚举、回溯
  • Heap's Algorithm
  • 固定-交换法
  • 字典法
  • 求第k个排列，计算法

Permutations

给一个无重数组，生成这个数组数字的全排列。

暴力循环法

一般最先想到的方法是暴力循环法，即对于每一位，遍历集合中可能的元素，如果在这一位之前出现过了该元素，跳过该元素。例如对于123，第一位可以是 1 或 2 或 3 。当第一位为 1时，第二位再遍历集合，发现 1 不行，因为前面已经出现 1 了，而 2 和 3 可以。当第二位为 2 时 ， 再遍历集合，发现 1 和 2都不行，3 可以。可以用递归或循环来实现，但是复杂度为 \(O(n^n)\) 。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
 // 典型的回溯方法

List<List<Integer>> result;
    private void helper(int[] nums, boolean[] used, List<Integer> preArr){
        if(preArr.size() == nums.length){
            List<Integer> one = new LinkedList<>();
            one.addAll(preArr);
            result.add(one);
        }
        for(int i = 0; i < nums.length; ++i){
           // 如果nums[i]被用过了，就跳过
            if(used[i]) continue;
            // 否则，加入到当前序列里
            preArr.add(nums[i]);
            used[i] = true;
            helper(nums,used,preArr);
            preArr.remove(preArr.size() - 1);
            used[i] = false;
        }
    }
    public List<List<Integer>> permute(int[] nums) {
        boolean[] used = new boolean[nums.length];
        result = new LinkedList<>();
        helper(nums,used,new LinkedList<>());
        return result;
    }

有没有更优雅的解法呢。

当然是有骚操作的。

Heap's Algorithm

Heap's Algorithm 是B. R. Heap在1963提出的一种全排列的算法。核心思想就是每次保持n - 2个元素不动，对剩余的两个元素进行交换。什么意思呢？我们以[a,b,c,d]这四个元素的全排列为例，首先，我们将元素d作为固定元素拿出来，对[a,b,c]进行全排列，而对[a,b,c]进行全排列的过程中，我们又将c作为固定元素拿出来，对元素a、b进行交换，这样就得到全排列的两种可能。同理，下一步是我们将b作为固定元素拿出来，对a、c进行交换。依次类推。这张图详细地展示了这一种算法思想，请参考。

可能有点不好理解。我们先看一下伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 保持第n个元素不动，对前n-1个元素进行全排列
generate(int n, int[] A){
  if n == 1 then
    output(A)
  else
    for(i = 0; i < n - 1; ++i){
      generate(n-1, A)
        if(n%2 == 0){ // 如果n是偶数，交换第i个和最后一个元素
          swap(A[i], A[n-1])
        }else{// 如果n是奇数，交换第1个和最后一个元素；
          swap(A[0], A[n-1])
        }
    }
    generate(n-1, A)
}

然而并不能看懂在干啥。

固定-交换法

还有一种思路，这个更好理解一丢丢：

n个数的全排列，一共有\(n!\)种情况. （n个位置，第一个位置有n种，当第一个位置固定下来之后，第二个位置有n-1种情况...）

全排列的过程：

  • 选择第一个字符
  • 获得第一个字符固定下来之后的所有的全排列
    • 选择第二个字符
    • 获得第一+ 二个字符固定下来之后的所有的全排列

从这个过程可见，这是一个递归的过程。

所以这种方式也是通过固定一个元素，进行剩余元素的交换。缺点是，每次交换过后需要再次交换以回到上一层数组。

代码较为简单些：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private void swap(int[] nums,int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    List<List<Integer>> result = new LinkedList<>();
    private void helper(int[] nums, int fixed){
        if(fixed == nums.length){
            List<Integer> one = new ArrayList<>(nums.length);
            for(int e : nums){one.add(e);}
            result.add(one);
            return;
        }
        // 将fixed依次与后面的元素交换
        for(int i = fixed; i < nums.length; ++i){
            swap(nums, i, fixed);
            helper(nums, fixed + 1);
            swap(nums, i, fixed);
        }
    }
    public List<List<Integer>> permute(int[] nums) {
        helper(nums,0);
        return result;
    }

Permutations II

follow up -- 如果输入数组有重复元素，输出全排列

暴力求解

由于这道题有重复元素，因此需要注意重复元素。

最暴力的方式就是先排序，然后当这个元素与上一次循环的元素一样时，跳过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
List<List<Integer>> result = new LinkedList<>();
    boolean[] used;
    private void helper(int[] nums,List<Integer> one, int i){
        if(i == nums.length){
            List<Integer> res = new ArrayList<>(nums.length);
            res.addAll(one);
            result.add(res);
            return;
        }
        int last = Integer.MIN_VALUE;
        for(int j = 0; j < nums.length; ++j){
            if(used[j] || (j > 0 && nums[j] == last)) continue; // 注意这里不可以用nums[j] == nums[j - 1] ！！！
            one.add(nums[j]);
            used[j] = true;
            helper(nums,one,i + 1);
            used[j] = false;
            one.remove(one.size() - 1);
            last = nums[j];
        }
    }
    public List<List<Integer>> permuteUnique(int[] nums) {
        used = new boolean[nums.length];
        Arrays.sort(nums);
        helper(nums,new ArrayList<Integer>(nums.length), 0);
        return result;
    }

固定-交换法

当然，这道题也可以借用上一题“交换”的想法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
private void swap(int[] nums,int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    List<List<Integer>> result = new LinkedList<>();

    private void helper(int[] nums, int i){
        if(i == nums.length){
            List<Integer> res = new ArrayList<>(nums.length);
            for(int e : nums){res.add(e);}
            result.add(res);
            return;
        }
        for(int j = i ; j < nums.length; ++j){
            // 一旦i~j之间有一个元素nums[k]与nums[j]相同，那就不用再交换了（因为nums[k] == nums[j],没有必要再次交换了
            boolean stop = false;
            for(int k = j - 1; k >= i; --k){
                if(nums[k] == nums[j]){
                    stop = true;break;
                }
            }
            if(stop)continue;
            // 将nums[i] 依次与nums[j]交换，然后固定nums[i]
            swap(nums, i, j);
            helper(nums, i + 1);
            swap(nums, i, j);

        }

    }
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);
        helper(nums, 0);
        return result;
    }

follow up - 字典顺序输出全排列

如果我们要求按照字典顺序输出全排列呢？

固定-交换法

假如按照上面固定交换法呢？

我们先看看固定-交换法的执行结果：

输入123，输出为：

1
2
3
4
5
6
0	[1, 2, 3]
1	[1, 3, 2]
2	[2, 1, 3]
3	[2, 3, 1]
4	[3, 2, 1]  -- x
5	[3, 1, 2]  -- x

我们发现最后两个输出的顺序不是字典顺序。这是因为在之前的交换中，当我们把3固定在首位时，此刻3之后的数字不是顺序了。所以生成有误。

那么我们做出一点改动，即在交换时，我们使用一种shift操作：

1
2
3
1 2 3 4
   ↓ shift
4 1 2 3

即保持原数组不变，只把后面的提到前面来

当然在递归结束，还要这样shift_back回去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
private void swap(int[] nums,int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    private void shift(int[] nums, int i, int j){
        // 将nums[j]挪到nums[i] , 然后将其余的后移
        int temp = nums[j];
        while (j > i){
            nums[j] = nums[j-1];
            --j;
        }
        nums[i] = temp;
    }
    private void shiftBack(int[] nums, int i, int j){
        // 将nums[i]挪到nums[j] , 然后将其余的左移
        int temp = nums[i];
        while (i < j){
            nums[i] = nums[i + 1];
            ++i;
        }
        nums[j] = temp;
    }
    int counter = 0;
    String result;
    int k;
    private void helper(int[] nums, int i){
        if(counter > k){
            return;
        }
        if(i == nums.length){
            ++counter;
            //System.out.println(counter + "\t" + Arrays.toString(nums));
            StringBuilder strBu = new StringBuilder();
            if(counter == k){
                for(int e : nums)strBu.append(e);
                result = strBu.toString();
            }
            return;
        }
        for(int j = i; j < nums.length; ++j){
            shift(nums, i, j);
            helper(nums, i + 1);
            shiftBack(nums, i ,j);
        }
    }
    public String getPermutation(int n, int k) {
        int[] nums = new int[n];
        for(int i = 0; i < n; ++i){
            nums[i] = i + 1;
        }
        this.k = k;
        helper(nums,0);
        return result;

    }

然后就万事大吉了！

然而，这种方式非常的慢。

我们还有一种优化，接着看下一题。

Next Permutation

输出指定数组的下一个排列

骚操作，字典法

这个算法的核心思想就是，对于每一种可能排列的情况，我们都想办法使其与某种顺序建立对应关系，这种关系式一一对应的，这样我们就能通过遍历得到的某种顺序来生成全排列，这样就能避免递归过程了。这种按照某种顺序来生成全排列的方法就被称为是字典序。

很显然，最重要的是如何才能找到这样一种一一对应的顺序关系，此处继续用\(a={0,1,2,3}\)来说明字典序算法的过程。

要找到一种顺序关系，我们就首先要定义大小关系，对于两个序列\({0,2,1,3}\)和\({0,2,3,1}\)来说，序列\({0,2,3,1}\)要比\({0,2,1,3}\)大，比较的方法是从前到后依次比较相同位置上的元素，如果相同则继续比较下一个元素，直到遇到一个不同的元素，元素值大的序列就大于元素值小的序列。按照这样的大小关系形成的序列的顺序，就是字典序。可以看到，最小的序列一定是\({0,1,2,3}\)，最大的序列是\({3,2,1,0}\)。而字典序算法就是从字典序中最小的序列开始，一直不停寻找下一个仅比上一个序列大的序列，直到到达最大的序列。[2]

现在问题变成了，如何从当前状态生成下一个状态？

假设当前排列是\(a[1.....n]\)

  1. 从\(a\)中找到满足\(a[k] < a[k + 1]\)（升序）的最后一个k。如果不存在，则\(a\)已经是字典序最大序列了。
  2. 在\(a[k + 1,....,n]\) 中寻找比\(a[k]\) 大的最小值\(a[j]\)。（在\(a[k+1,...,n]\) 中，\(a[k]\) 仅次于\(a[j]\) 的数字。将它们交换后，能保证整个序列是最小增长的）
  3. 交换\(a[k]与a[j]\) ，并将\(a[k,...,n]\) 全部排序

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
private void swap(int[] nums,int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    public void nextPermutation(int[] nums) {
        int n = nums.length;
        // 寻找nums的下一个排列
        // 寻找最后一个升序nums[q]
        int q = -1;
        for(int i = 1; i < n; ++i){
            if(nums[i - 1] < nums[i]){
                q = i - 1 ;
            }
        }
        if(q == -1){ // 此刻nums是最后一个排列
            int start = 0, end = n-1;
            while (start + 1 < end){
                swap(nums,start,end);
                ++start; --end;
            }
            if(start + 1 == end){swap(nums,start,end);}
        }
        else {
            // 寻找比nums[q]大的最小值nums[m]
            int m = q, min = Integer.MAX_VALUE;
            int i = q;
            while (i < n) {
                if (nums[i] > nums[q] && nums[i] < min) {
                    min = nums[i];
                    m = i;
                }
                ++i;
            }
            // 将nums[q]与nums[m]交换
            swap(nums, q, m);
            // 将[q + 1 ~ n]倒排
            Arrays.sort(nums, q + 1, n);
            // 输出nums
        }
    }

当然有一种优化思路是，优化第1步中：将”从前到后寻找最后一个升序“转化为”从后到前寻找第一个降序“。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public void nextPermutation(int[] nums) {
        int n = nums.length;
        // 寻找nums的下一个排列
        // 寻找最后一个升序nums[q]
        int q = nums.length;
        for(int i = n - 1; i > 0; --i){
            if(nums[i - 1] < nums[i]){
                q = i - 1 ;
                break;
            }
        }
        if(q == nums.length){ // 此刻nums是最后一个排列
            int start = 0, end = n-1;
            while (start + 1 < end){
                swap(nums,start,end);
                ++start; --end;
            }
            if(start + 1 == end){swap(nums,start,end);}
        }
        else {
            // 寻找比nums[q]大的最小值nums[m]
            int m = q, min = Integer.MAX_VALUE;
            int i = q;
            while (i < n) {
                if (nums[i] > nums[q] && nums[i] < min) {
                    min = nums[i];
                    m = i;
                }
                ++i;
            }
            // 将nums[q]与nums[m]交换
            swap(nums, q, m);
            // 将[q + 1 ~ n]倒排
            Arrays.sort(nums, q + 1, n);
            // 输出nums
        }
    }

Next Greater Element III

给一个数，输出这个数的所有排列中刚好比这个数稍微大一点的数。

这对我来说还是有点难度的。需要一点技巧。想要生成稍微大一点的数，那就要从低位下手。例如一个数是***132000，那么把1和2交换就可以得到一个稍微大一点的数。而我们需要确保以下几点：

  1. '1' 一定是从右往左看第一个递减的数
  2. '2' 一定是1右边的那个稍微比1大一点点的数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
 public int nextGreaterElement(int n) {

    // 样例 230241  -> 230412

    char[] number = (n + "").toCharArray(); // 这简直是骚操作了
    // 从个位开始，依次寻找第一次递减的两个数
    int i = number.length - 1;
    for(i = number.length - 1; i > 0; --i){
        if(number[i-1] < number[i] ) break;// 找到number[i-1] = 2
    }
    if(i == 0) return -1;

    // 从(i,number.length)找到比i-1大的最小的数，放在i-1的位置。
    // 这样就能确保现在生成的数字是最小的
    int smallest = i;
    for(int j = i + 1; j < number.length; ++j){
        if(number[j] > number[i - 1] && number[j] <= number[smallest])
            smallest = j;
    }
    // 将largestIdx与i-1交换
    char temp = number[smallest];
    number[smallest] = number[i - 1];
    number[i - 1] = temp;
    // 将剩下的数字排序
    Arrays.sort(number, i, number.length);

    // 转化为数字
    long val = Long.parseLong(new String(number));
    return (val <= Integer.MAX_VALUE) ? (int) val : -1;
}

Permutation Sequence

输出1-n数字组成的数字中的字典序第k个排列

思路一：如果用follow up 的代码，是完全可以的。只是时间非常高。

思路二：字典法，依次输出，时间代价还是很昂贵，还有可能超时

思路三：骚操作

n个数的全排列一共有\(n!\) 个。基于这个性质我们可以计算出某一位对应的数字是几！骚操作啊！

我们用123来举例。它的全排列为：

1
2
3
4
5
6
7
            第一位           第二位
0  123     1 = nums[0/2]      2
1  132     1 = nums[1/2]      3
2  213     2 = nums[2/2]      1
3  231     2 = nums[3/2]      3
4  312     3 = nums[4/2]      1    
5  321     3 = nums[5/2]      2    <-- k = 5

因为当第一位确定时，全排列个数为\((n-1)! = 2\) 个。

所以第一位的重复周期是\((n-1)!\) 。那么第k个就是\(\frac{k}{(n-1)!}\) 。

假如第一位是a1 = 3，那么第一位是1和2的全排列都可以去除了！那就是从3开头的全排列中寻找第\(k' = k - (a1-1) * (n-1)! = k \text{ % } (n-1)! = 5 - 4 = 1\) 个！

而且，当第一位确定时，第二位只剩下\(n - 1\) 个数字可以选择。因此以3开头的只有\((n-2)!\) 种。所以第二位的数字为\(\frac{k`}{(n-2)!}\)

然后我们就找到了规律！

a1 = k / (n - 1)! k1 = k

a2 = k1 / (n - 2)! k2 = k1 % (n - 2)! ...

an-1 = kn-2 / 1! kn-1 = kn-2 / 1!

an = kn-1 / 0! kn = kn-1 % 0!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public String getPermutation(int n, int k) {
        ArrayList<Integer> candidates = new ArrayList<>(n);
        for(int i = 1; i <= n; ++i){
            candidates.add(i);
        }
        // 先存下来n!
        int[] factorial = new int[n + 1];
        factorial[0] = 1;
        factorial[1] = 1; // factorial[i] = i!
        for(int i = 2; i <= n; ++i){
            factorial[i] = factorial[i-1] * i;
        }
        // 计算第k位
        k = k - 1;
        StringBuilder stringBuilder = new StringBuilder();
        for(int i = 0; i < n; ++i){
            int idx = k / factorial[n-1-i] ;
            stringBuilder.append(candidates.get(idx));
            candidates.remove(idx); // 注意维护剩余集合
            k = k % factorial[n-1-i];
        }
        return stringBuilder.toString();
    }

Binary Watch

有一种二进制的表。其中用4个位数表示小时（0-11），用6个位数表示分钟（0-59）。

给一个n，表示当前亮灯的个数。求可能出现的时刻

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
private void permutations(int[] candidates, int idx, int num, int sum, List<Integer> result, int limit){
    //从候选集里选num个，求相加有多少种结果
    if(sum >= limit)return;
    if(num == 0){result.add(sum);return;}
    if(idx >= candidates.length || candidates.length - idx < num)return;
    for(int i = idx; i < candidates.length; ++i){
        permutations(candidates, i + 1, num - 1, sum + candidates[i], result, limit);
    }
}
private List<String> helper(int h_num, int m_num, int[] h, int[] m){
    // h_num个小时灯，m_num个分钟灯
    List<Integer> hours = new LinkedList<>();
    permutations(h, 0, h_num, 0, hours, 12);
    List<Integer> minites = new LinkedList<>();
    permutations(m, 0, m_num, 0, minites, 60);
    //两两组合
    List<String> result = new LinkedList<>();
    for(Integer hour : hours){
        String hour_str = Integer.toString(hour);
        for(Integer minite : minites){
            String min_str = minite < 10 ? "0"+Integer.toString(minite) : Integer.toString(minite);
            result.add(hour_str + ":" + min_str);
        }
    }
    return result;
}
public List<String> readBinaryWatch(int num) {
    int[] h = {1,2,4,8};
    int[] m = {1,2,4,8,16,32};
    List<String> result = new LinkedList<>();
    for(int h_num = 0; h_num < 4; ++h_num){
        int m_num = num - h_num;
        if(m_num > 6)continue;
        result.addAll(helper(h_num, m_num, h, m));
    }
    return result;
}

Sliding Puzzle

给一个2*3的数组，其中元素是0、1、2、3、4 、5。每次只能将0与周围的4个位置交换。求问给定数组最少交换多少次，可以将数组交换为123450

思路：回溯法 + 记忆化搜索

要点：记忆化搜索里存储的内容是：从原数组走到现在，已经走了多少步！（这一点想了很久都没有想通。自己陷入了怪圈）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    Map<Integer, Integer> map = new HashMap<>(); // 从原数组走到key，已经走了多少步
    int min_move = Integer.MAX_VALUE;
    public int slidingPuzzle(int[][] board) {
        map.put(123450, 0);
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 3; j++) {
                if (board[i][j] == 0) {
                    helper(board, i,j, 0);
        			return min_move == Integer.MAX_VALUE ? -1 : min_move;
                }
            }
        }
        
    }
    private void helper(int[][] board, int x, int y, int move) {
        // 如果走到key时步数已经大于最小步数了，那就没有必要再继续走了
        if (move > min_move) return;
        int code = encode(board);
        if (code == 123450) {
            min_move = move;
            return;
        }
        if (map.containsKey(code)) {
            // 如果这次的move步数大于之前另一种方式move到code的步数，那就没有必要再继续走了
            if (move > map.get(code)) return;
        }
        map.put(code, move);
        for (int[] dir : dirs) {
            int nx = x + dir[0], ny = y + dir[1];
            if (nx >= 0 && nx < 2 && ny >= 0 && ny < 3) {
                swap(board, x, y, nx, ny);
                helper(board, nx, ny, move + 1);
                swap(board, nx, ny, x, y);
            }
        }
    }
    private void swap (int[][] board, int i, int j, int ii, int jj) {
        int temp = board[i][j];
        board[i][j] = board[ii][jj];
        board[ii][jj] = temp;
    }
    private int encode(int[][] board) {
        int code = 0;
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 3; j++) {
                code *= 10;
                code += board[i][j];
            }
        }
        return code;
    }

元素和、组合问题

Combinations

用1-n的数字，每次拿k个。输出所有的组合方式。

相当经典的回溯问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
List<List<Integer>> result = new LinkedList<>();
    private void helper(int n, int k, int start, List<Integer> candidates){
        if(k == 0){
            result.add(new ArrayList<>(candidates));
            return;
        }
        for(int i = start; i <= n; ++i){
            candidates.add(i);
            helper(n, k - 1, i + 1, candidates);
            candidates.remove(candidates.size() - 1);
        }
    }
    public List<List<Integer>> combine(int n, int k) {
        helper(n, k, 1, new LinkedList<>());
        return result;
    }

在leetcode上看到还有一种思路，很快。但总体复杂度其实差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public List<List<Integer>> combine(int n, int k) {
    List<Integer> current = new ArrayList<>();
    List<List<Integer>> result = new ArrayList<>();
    dfs(result, current, 1, n, k);
    return result;
}

void dfs(List<List<Integer>> result, List<Integer> current, int c, int n, int k) {
    if (c + k > n + 1) {
        return;
    }
    if (k == 0) {
        List<Integer> tmpList = new ArrayList<>(current);
        result.add(tmpList);
        return;
    }
   // 使用c这个数字
    current.add(c);
    dfs(result, current, c + 1, n, k - 1);
    current.remove(current.size() - 1);
    // 不使用c这个数字
    dfs(result, current, c + 1, n, k);
}

Combination Sum

给一个数组和一个target.求数组中的元素和等于target的所有可能。元素可以多次取。

思路：典型的回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
List<List<Integer>> result = new LinkedList<>();
    private void helper(int[] candidates, int target, int start, ArrayList<Integer> added){
        if(target < 0)return;
        if(target == 0){
            List<Integer> aRes = new ArrayList<>(added.size());
            aRes.addAll(added);
            result.add(aRes);
            return;
        }
       // 从start开始取（start就是上一次使用的元素）
        for(int i = start; i < candidates.length; ++i){
            added.add(candidates[i]);
            helper(candidates, target - candidates[i], i,added);
            added.remove(added.size() - 1);
        }
    }
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        helper(candidates,target, 0,new ArrayList<>(candidates.length));
        return result;
    }

虽然说这道题可以用dp来简化。但是由于重复的边界条件实在是难以处理，所以还是弃用了。

Combination Sum II

给一个有重数组和一个target.求数组中的元素和等于target的所有可能。元素不可以多次取。

这道题与上一题的最大区别就是不能多次取！需要注意的地方就是递归进入时的i需要加一（跳过本元素）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
List<List<Integer>> result = new LinkedList<>();
    private void helper(int[] candidates, int target, int start, List<Integer> selected){
        if(target < 0) return;
        if(target == 0){
            List<Integer> one = new ArrayList<>(selected);
            result.add(one);
            return;
        }
        for(int i = start; i < candidates.length; ++i){
            if(i > start  && candidates[i] == candidates[i - 1])continue; // 去重
            if(target - candidates[i] < 0)break;// 剪枝
            // 回溯
            selected.add(candidates[i]);
            helper(candidates, target - candidates[i], i + 1,selected); // 从i + 1处继续
            selected.remove(selected.size() - 1);
        }
    }
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        helper(candidates,target, 0, new LinkedList<>());
        return result;
    }

Combination Sum III

求k个数（0-9的数）的和为n的所有组合。

还是回溯问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
List<List<Integer>> result = new LinkedList<>();

    private void helper(int k, int start, int target, List<Integer> candidates){
        if(target < 0 || k < 0) return;
        if(target == 0 && k == 0){
            result.add(new ArrayList<>(candidates));
            return;
        }
        for(int i = start; i <= 9; ++i){
            if(target - i < 0) break; // 剪枝
            candidates.add(i);
            helper(k - 1,i + 1, target - i, candidates);
            candidates.remove(candidates.size() - 1);
        }
    }
    public List<List<Integer>> combinationSum3(int k, int n) {
        helper(k,1, n, new LinkedList<>());
        return result;
    }

当然还可以用另一种思路，就是选或者不选的问题。这种思路类似Combinations的第二种解法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
List<List<Integer>> result = new LinkedList<>();

    private void helper(int k, int i, int target, List<Integer> candidates){
        if(target == 0 && k == 0){
            result.add(new ArrayList<>(candidates));
            return;
        }
        if(k == 0 && target != 0){return;}
        if(i > 9 || target < 0 || k < 0) return;
        // 选i
        candidates.add(i);
        helper(k - 1,i + 1, target - i, candidates);
        candidates.remove(candidates.size() - 1);
        // 不选i
        helper(k,i + 1, target, candidates);

    }
    public List<List<Integer>> combinationSum3(int k, int n) {
        helper(k,1, n, new LinkedList<>());
        return result;
    }

Increasing Subsequences

给一个有重数组，输出所有的递增子序列

思路：回溯法

注意点：由于数组有重，则一定要判断重复！例如数组[1,3,2,3] ，如果不判断重复，就会出现两个[1,3]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
List<List<Integer>> result = new LinkedList<>();
private void helper(int[] nums, int idx,List<Integer> added, int lastAdd, HashSet<Integer> hash){

    if(idx >= nums.length){
        return;
    }

    for(int i = idx; i < nums.length; ++i){
        if(hash.contains(nums[i]))continue;
        if(nums[i] >= lastAdd) {
            hash.add(nums[i]);
            added.add(nums[i]);
            if(added.size() >= 2) {
                result.add(new ArrayList<>(added));
            }
            helper(nums, i + 1, added, nums[i], new HashSet<>());
            added.remove(added.size() - 1);
        }else
            helper(nums, i + 1, added, lastAdd, hash);

    }
}
public List<List<Integer>> findSubsequences(int[] nums) {
    helper(nums, 0, new LinkedList<>(), Integer.MIN_VALUE, new HashSet<>());
    return result;
}

其它问题

Count Numbers with Unique Digits

给一个n。求x的个数，其中\(0<= x <= 10^n\) ，且x的每一位的数字都不相同。

思路：x是n位数，且每位都不相等。

如果n大于10，那\(x > 10^{10}\) 的都不用考虑了

如果n小于等于10，那就考虑0-9能组成多少个n位的数字了！

这道题完全可以用公式完成：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
n位数的可能有如下：

0      （就是0）
1 位数 -> C(9,1)  (从1-9里随机挑选一个)
2 位数 -> C(9,1) * C(9,1)  (第一位从1-9挑，第二位与第一位不同即可，所以也是9种)
3 位数 -> C(9,1) * C(9,1) * C(8,1) (第一位从1-9挑，第二位与第一位不同，第三位与前两位不同)
...
n 位数

代码：
    //  * C(9,1) * C(8,1) *....
	private int helper(int n, int k){
        if(k == 0 || n == 0) return 1;
        return k * helper(n - 1, k - 1);
    }

    public int countNumbersWithUniqueDigits(int n) {
        int sum = 1;
        for(int i = 1; i <= n; ++i){
            sum += 9 * helper(i - 1, 9);
        }
        return sum;
    }

Letter Combinations of a Phone Number

求手机“九宫格”输入数字后组成的字符串的所有可能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
HashMap<Character, String[]> table = new HashMap<>();
    private void buildTable(){
        table.put('1',new String[0]);
        table.put('2',new String[]{"a","b","c"});
        table.put('3',new String[]{"d","e","f"});
        table.put('4',new String[]{"g","h","i"});
        table.put('5',new String[]{"j","k","l"});
        table.put('6',new String[]{"m","n","o"});
        table.put('7',new String[]{"p","q","r","s"});
        table.put('8',new String[]{"t","u","v"});
        table.put('9',new String[]{"w","x","y","z"});
        table.put('0',new String[]{" "});
        table.put('#',new String[]{"#"});
        table.put('*',new String[]{"*"});
    }
    public List<String> letterCombinations(String digits) {
        List<String> result = new LinkedList<>();
        if(digits.length() == 0) return result;
        buildTable();
        char[] digits_c = digits.toCharArray();
        // 初始化
        String[] candicates = table.get(digits_c[0]);
        for(String c : candicates){
            String aRes = new String(c);
            result.add(aRes);
        }
        // 插入
        for(int i = 1; i < digits_c.length; ++i){
            candicates = table.get(digits_c[i]);
            // 依次将candicates与builder的每个元素组合
            List<String> result_curr = new LinkedList<>();
            for(String aRes : result){
                for(String c : candicates){
                    String aRes_curr = aRes + c;
                    result_curr.add(aRes_curr);
                }
            }
            result = result_curr;
        }
        return result;
    }

Generate Parentheses

有n对括号。求所有括号可能的摆放次序（括号必须成对先后出现）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
List<String> result = new LinkedList<>();
    private void helper(int remain_left, int remain_right, StringBuilder builder){
        if(remain_left == 0 && remain_right == 0){
            result.add(builder.toString());
            return;
        }
        if(remain_left == 0){
            builder.append(')');
            helper(remain_left, remain_right - 1, builder);
            builder.delete(builder.length() - 1, builder.length());
            return;
        }
        if(remain_left >= remain_right || remain_right == 0){
            builder.append('(');
            helper(remain_left - 1, remain_right, builder);
            builder.delete(builder.length() - 1, builder.length());
            return;
        }
        // 要么放一个左括号
        builder.append('(');
        helper(remain_left - 1, remain_right, builder);
        builder.delete(builder.length() - 1, builder.length());
        // 要么放一个右括号
        builder.append(')');
        helper(remain_left, remain_right - 1, builder);
        builder.delete(builder.length() - 1, builder.length());

    }
    public List<String> generateParenthesis(int n) {
        helper(n,n,new StringBuilder());
        return result;
    }

优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
List<String> result = new LinkedList<>();
    private void helper(int remain_left, int remain_right, StringBuilder builder){
        if(remain_left == 0 && remain_right == 0){
            result.add(builder.toString());
            return;
        }
        if(remain_left > 0){ // 只要左括号有富裕，就可以放
            builder.append('(');
            helper(remain_left - 1, remain_right, builder);
            builder.delete(builder.length() - 1, builder.length());
        }
        if(remain_left < remain_right) { // 左括号比右括号多时，才可以放右括号
            builder.append(')');
            helper(remain_left, remain_right - 1, builder);
            builder.delete(builder.length() - 1, builder.length());
        }
    }
    public List<String> generateParenthesis(int n) {
        helper(n,n,new StringBuilder());
        return result;
    }

Valid Sudoku

判断当前给出的数独格子是否符合数独要求（只要判断当前已经填入的空格是否符合要求即可）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
boolean[][] eachRow = new boolean[10][10];
boolean[][] eachCol = new boolean[10][10];
boolean[][] eachSquare = new boolean[10][10];


public boolean isValidSudoku(char[][] board) {
  for(int i = 0; i < board.length; ++i){
    for(int j = 0; j < board[0].length; ++j){
      if(board[i][j] == '.') continue;
      if(eachCol[j][board[i][j] - '0'] ||
         eachRow[i][board[i][j] - '0'] ||
         eachSquare[i/3 + 3*(j/3)][board[i][j] - '0']) return false;
      eachCol[j][board[i][j] - '0'] = true;
      eachRow[i][board[i][j] - '0'] = true;
      eachSquare[i/3 + 3*(j/3)][board[i][j] - '0'] = true;
    }
  }
  return true;
}

Sudoku Solver

\(9 \times 9\) 的数独，填入数字1-9，要求行列不重复，且每个宫内不重复。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
boolean[][][] used;
    /**used[0][i][q] : 第i列,数字q是否被使用
     * used[1][i][q] : 第i行，数字q是否被使用
     * used[2][i][q] : 第i个宫中数字q是否被使用
     * **/
    private boolean helper(char[][] board, int filled){
        if(filled == board.length * board.length){
            return true;
        }
        for(int i = 0; i < board.length; ++i){
            for(int j = 0; j < board.length; ++j){
                if(board[i][j] != '.') continue;
                //尝试给board[i][j]填入数字q
                for(int q = 1; q <= 9; ++q){
                    if(used[0][i][q] || used[1][j][q] || used[2][j/3 + 3 * (i/3)][q]) continue;
                    board[i][j] = (char)(q + 48);
                    used[0][i][q] = true;
                    used[1][j][q] = true;
                    used[2][j/3 + 3 * (i/3)][q] = true;
                    if(helper(board, filled + 1))return true;
                    board[i][j] = '.';
                    used[0][i][q] = false;
                    used[1][j][q] = false;
                    used[2][j/3 + 3 * (i/3)][q] = false;
                }
                //这个剪枝很重要
                //board[i][j]填任何数字都不行
                return false;
            }
        }
        return false;
    }
    public void solveSudoku(char[][] board) {
        used = new boolean[3][board.length][10];
        //初始化
        int filled = 0;
        for(int i = 0; i < board.length; ++i){
            for(int j = 0; j < board.length; ++j){
                if(board[i][j] == '.')continue;
                used[0][i][board[i][j]-48] = true;
                used[1][j][board[i][j]-48] = true;
                used[2][j/3 + 3 * (i/3)][board[i][j]-48] = true;
                ++filled;
            }
        }
        helper(board,filled);
    }

Beautiful Arrangement

给1-N的数字，填入长度为N的数组。令数组的idx从1开始。要求：idx能整除nums[idx]或nums[idx]能整除idx。求所有的可能数。

思路：一开始想多了。其实用暴力遍历就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int counter = 0;
    private void helper(int idx, boolean[] used, int N){
        if(idx == used.length){
            ++counter;
        }
        for(int i = 1; i <= N; ++i){
            if(used[i])continue;
            if(idx % i == 0 || i % idx == 0){
                used[i] = true;
                helper(idx + 1, used, N);
                used[i] = false;
            }
        }
    }
    public int countArrangement(int N) {
        boolean[] used = new boolean[N + 1];
        helper(1, used, N);

        return counter;
    }

Wildcard Matching

给两个字符串，其中一个含有*或?。*代表可匹配任意多个字符。?代表可匹配任意元素。求两个字符串是否能完全匹配

思路：回溯，碰到不行的就回退

最后几个样例会超时，所以我又用了dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
private int helper(String s, String p, int s_idx, int p_idx){
    if(s_idx >= s.length() && p_idx >= p.length()) return 1;
    if(p_idx >= p.length()) return -1;
    if(s_idx >= s.length()){
        while (p_idx < p.length()) {
            if (p.charAt(p_idx) == '*')
                ++p_idx;
            else return -1;
        }
        return 1;
    }

    if(dp[s_idx][p_idx] != 0) return dp[s_idx][p_idx];

    char s_element = s.charAt(s_idx);
    char p_element = p.charAt(p_idx);

    if(p_element == '?'){
        dp[s_idx][p_idx] = helper(s, p, s_idx + 1, p_idx + 1);
    }else if(p_element == '*'){
      // 跳过连续的******
        while (p_idx < p.length() - 1){
            if(p.charAt(p_idx + 1) == '*') ++p_idx;
            else break;
        }
        dp[s_idx][p_idx] = helper(s, p, s_idx, p_idx + 1);
        if(dp[s_idx][p_idx] == -1)
            dp[s_idx][p_idx] = helper(s, p, s_idx + 1, p_idx);
    }else if(p_element == s_element){
        dp[s_idx][p_idx] = helper(s, p, s_idx + 1, p_idx + 1);
    }else
        dp[s_idx][p_idx] = -1;
    return dp[s_idx][p_idx];
}
int[][] dp;
public boolean isMatch(String s, String p) {
    dp = new int[s.length()][p.length()];
    return helper(s, p, 0, 0) == 1;
}

二刷：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
private int helper(String s, String p, int s_idx, int p_idx){
     if(memo[s_idx][p_idx] != 0) return memo[s_idx][p_idx];
     if(s_idx == s.length() && p_idx == p.length()){
         memo[s_idx][p_idx] = 1;
         return  memo[s_idx][p_idx];
     }
     if(p_idx == p.length()) {
         memo[s_idx][p_idx] = -1;
         return memo[s_idx][p_idx];
     }
     if(s_idx == s.length()){
         while (p_idx < p.length() && p.charAt(p_idx) == '*') {++p_idx;}
         memo[s_idx][p_idx] = p_idx == p.length() ? 1 : -1;
         return  memo[s_idx][p_idx];
     }

     if(p.charAt(p_idx) == '?' || s.charAt(s_idx) == p.charAt(p_idx)){
         memo[s_idx][p_idx] =  helper(s,p, s_idx + 1, p_idx + 1);

     }else if(p.charAt(p_idx) == '*'){
         memo[s_idx][p_idx] = helper(s, p, s_idx + 1, p_idx);
         if(memo[s_idx][p_idx] < 0)
             memo[s_idx][p_idx] = helper(s, p, s_idx, p_idx + 1);
     }else{
         memo[s_idx][p_idx] = -1;
     }
     return memo[s_idx][p_idx];
 }
 int[][] memo;
 public boolean isMatch(String s, String p) {
     memo = new int[s.length() + 1][p.length() + 1];
     helper(s, p ,0,0);
     return memo[s.length()][p.length()] == 1;
 }

Regular Expression Matching

给两个字符串，其中一个含有*或.。*代表可匹配前一个元素0个或多个。.代表可匹配任意元素。求两个字符串是否能完全匹配

思路：回溯，碰到不行的就回退

注意边界条件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
private boolean helper(String s, String p, int s_idx, int p_idx){
        if(s_idx < 0 && p_idx < 0) return true;
        if(p_idx < 0) return false;
        if(s_idx < 0){
            if(p.charAt(p_idx) == '*')
                return helper(s, p, s_idx, p_idx - 2); // 匹配0个
            else return false;
        }
        char p_element = p.charAt(p_idx);
        char s_element = s.charAt(s_idx);
        if(p_element == '.'){
            return helper(s, p, s_idx - 1, p_idx - 1);
        }else if(p_element == '*'){
            // 比较s[s_idx]与p[p_idx - 1]
            if(p_idx == 0) return true;
            if((s_element == p.charAt(p_idx - 1)) || (p.charAt(p_idx - 1) == '.')){
                return helper(s, p, s_idx - 1,p_idx) || // 匹配1个
                        helper(s, p, s_idx, p_idx - 2); // 匹配0个
            }else{
                return helper(s, p, s_idx, p_idx - 2); // 匹配0个
            }
        }else{
            if(p_element == s_element){
                return helper(s, p, s_idx - 1, p_idx - 1);
            }else
                return false;
        }
    }
    public boolean isMatch(String s, String p) {
        return helper(s, p, s.length() - 1,p.length() - 1);
    }

Reconstruct Itinerary

行程安排问题。一个人从JFK出发，求一种能走得通的行程

这道题写了很久，一开始陷入了拓扑排序的怪圈。以后要注意自己的思维，不要被之前的题限制！

思路：

  1. 建立每个点的邻接列表
  2. 依次往下探测，遇到不合适的就返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Node implements Comparable<Node>{
    String departure;
    ArrayList<Node> neighbors = new ArrayList<>();
    boolean[] visited;
    Node(String departure){
        this.departure = departure;
    }

    @Override
    public int compareTo(Node o) {
        return this.departure.compareTo(o.departure);
    }
}
private HashMap<String, Node> countDegree(String[][] tickets){
    HashMap<String, Node> hashMap = new HashMap<>();
    for(String[] edge : tickets){
        hashMap.put(edge[0], new Node(edge[0]));
        hashMap.put(edge[1], new Node(edge[1]));
    }
    for(String[] edge : tickets){
        Node neibor = hashMap.get(edge[1]);
        hashMap.get(edge[0]).neighbors.add(neibor);
    }
    // 对每个departures的邻居排序
    for(Node e : hashMap.values()){
        Collections.sort(e.neighbors);
        e.visited = new boolean[e.neighbors.size()];
    }
    return hashMap;
}
private boolean dfs(Node departure, List<String> result, int length){
    //System.out.println(result);
    if(result.size() == length) return true;
    else if(result.size() > length) return false;
    for(int i = 0; i < departure.visited.length; ++i){
        if(departure.visited[i])continue;
        departure.visited[i] = true;
        result.add(departure.neighbors.get(i).departure);
        if(dfs(departure.neighbors.get(i), result, length)) return true;
        result.remove(result.size() - 1);
        departure.visited[i] = false;
    }
    return false;
}
public List<String> findItinerary(String[][] tickets) {
    //统计每个站邻居，并做排序
    HashMap<String, Node> departures = countDegree(tickets);
    // 开始做dfs
    List<String> result = new ArrayList<>(2 + tickets.length - 1);
    result.add("JFK");
    dfs(departures.get("JFK"), result, 2 + tickets.length - 1);
    return result;
}

用优先队列

下面这个方法真是太鸡贼了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public List<String> findItinerary(String[][] tickets) {
    for (String[] ticket : tickets)
        targets.computeIfAbsent(ticket[0], k -> new PriorityQueue()).add(ticket[1]);
    visit("JFK");
    return route;
}

Map<String, PriorityQueue<String>> targets = new HashMap<>();
List<String> route = new LinkedList();

void visit(String airport) {
    while(targets.containsKey(airport) && !targets.get(airport).isEmpty())
        visit(targets.get(airport).poll());
    route.add(0, airport); // 这里很巧妙
  // 1. 假设这条路下去是个环路，走回来了，那就暂时先不加，继续从环路递归
  // 2. 加入这条路不是个环路，那就加进去，然后跳出循环，回到环路，再把环路的结果依次相加
}

还有一种非递归，用栈的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public List<String> findItinerary(String[][] tickets) {
    Map<String, PriorityQueue<String>> targets = new HashMap<>();
    for (String[] ticket : tickets)
        targets.computeIfAbsent(ticket[0], k -> new PriorityQueue()).add(ticket[1]);
    List<String> route = new LinkedList();
    Stack<String> stack = new Stack<>();
    stack.push("JFK");
    while (!stack.empty()) {
        while (targets.containsKey(stack.peek()) && !targets.get(stack.peek()).isEmpty())
            stack.push(targets.get(stack.peek()).poll());
        route.add(0, stack.pop());
    }
    return route;
}

Matchsticks to Square

给一个数组，值表示火柴长度。求这些火柴能不能组成正方形。

有意思的题目。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private boolean dfs(int[] nums, boolean[] visited, int idx, int sum, int width, int counter){
    if(sum > width)return false;
    if(counter >= 4)return true;
    if(sum == width){
        ++counter;
        if(counter == 4)return true;
        idx = 0; //这里比较有意思
        sum = 0; // 有意思哇
    }
    if(idx >= nums.length || nums[idx] > width) return false;
    for(int i = idx; i < nums.length; ++i){
        if(visited[i])continue;
        if(nums[i] > width)return false;
        visited[i] = true;
        if(dfs(nums, visited, i + 1, sum + nums[i], width,counter))return true;
        visited[i] = false;
    }
    return false;
}
public boolean makesquare(int[] nums) {
    int sum = 0;
    for(int num : nums) sum += num;
    if(sum % 4 != 0) return false;
    int width = sum/4;
    return dfs(nums, new boolean[nums.length], 0, 0, width, 0);
}

Maximum Length of Pair Chain

假设有整数对[a,b]和[c,d] 。如果b < c ，那么这两个整数对可以构成一个链。给一些整数对，求这些整数对能构成的最长链。

思路：排序+记忆化搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
   int[] memo;
// memo[i]表示[i,n]的整数对能构成的最长链
   private int helper(int[][] pair, int idx, int[] lastPair){
       if(idx >= pair.length) return 0;
       if(memo[idx] >= 0) return memo[idx];
       // [lastPair[0], lastPair[1]]  , [pairidx[0], pairidx[1]]
       // 如果这两个整数对可以构成链，则尝试构成
       if(lastPair[1] < pair[idx][0]){
           memo[idx] = helper(pair, idx + 1, pair[idx]) + 1;
       }
       // 跳过这个整数对
       memo[idx] = Math.max(memo[idx], helper(pair, idx + 1, lastPair));
       return memo[idx];
   }
   public int findLongestChain(int[][] pairs) {
       // 先按照第2个元素排序
       Arrays.sort(pairs, new Comparator<int[]>() {
           @Override
           public int compare(int[] o1, int[] o2) {
               return o1[1] - o2[1];
           }
       });
       memo = new int[pairs.length];
       Arrays.fill(memo, -1);
       return helper(pairs, 0, new int[]{Integer.MIN_VALUE, Integer.MIN_VALUE});
   }

参考文献

  1. 全排列的经典算法-heap's algorithms
  2. 全排列算法part1
  3. [Leetcode] Permutation Sequence 全排列序列
  4. [LeetCode]76. Permutation Sequence全排列序列