大纲
- Graph
- Clone Graph
- Topological Sorting 拓扑排序
- 搜索
- DFS
- BFS 两个场景
- 图的遍历,Graph Traversal
- 简单图求最短路径,Shortest Path in Simple Graph
例题1,Clone Graph
克隆图!
方法——DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
if(node == null) return null;
Map<UndirectedGraphNode, UndirectedGraphNode> map = new HashMap<>();
return dfs(node, map);
}
public UndirectedGraphNode dfs(UndirectedGraphNode node, Map<UndirectedGraphNode, UndirectedGraphNode> map) {
if(map.containsKey(node)) return map.get(node);
UndirectedGraphNode newNode = new UndirectedGraphNode(node.label);
map.put(node, newNode);
List<UndirectedGraphNode> newNeighbors = newNode.neighbors;
for(UndirectedGraphNode neighbor: node.neighbors) {
newNeighbors.add(dfs(neighbor, map));
}
return newNode;
}
|
方法2——BFS + 队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| public UndirectedGraphNode cloneGraph(UndirectedGraphNode startNode) {
if(startNode == null) return null;
ArrayList<UndirectedGraphNode> nodes = new HashMap<>();
HashMap<UndirectedGraphNode, UndirectedGraphNode> mapping = new HashMap<>();
for(UndirectedGraphNode node : nodes){
UndirectedGraphNode newNode = new UndirectedGraphNode(node.val);
mapping.put(node, newNode);
}
for(UndirectedGraphNode node: nodes){
UndirectedGraphNode newNode = mapping.get(node);
for(UndirectedGraphNode neighbor : node.neighbors){
newNode.neighbors.add(mapping.get(neighbor));
}
}
return mapping.get(startNode);
}
private ArrayList<UndirectedGraphNode> bfs(UndirectedGraphNode startNode){
Queue<UndirectedGraphNode> queue = new LinkedList<>();
HashSet<UndirectedGraphNode> visited = new HashSet<>();
queue.offer(startNode);
visited.add(startNode);
while(!queue.isEmpty()){
UndirectedGraphNode head = queue.poll();
for(UndirectedGraphNode neibor : head.neighbors){
if(visited.contains(neibor)){ continue; }
queue.offer(neibor);
visited.add(neibor);
}
}
return new ArrayList<UndirectedGraphNode>(visited);
}
|
拓扑排序
下面这个图假设是一种上课顺序,比如上1之前必须上0。求这个图的任意一个拓扑排序(按照这个顺序上课则可以上完所有课)
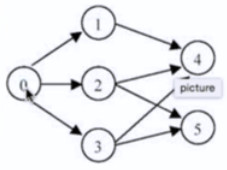
拓扑排序很好的参考资料:Topological Sort of a Graph
拓扑排序的思路如下:
- 统计当前入度为0的点,加入队列
- 将当前所有入度为0的点删掉,并将这些点的下一点的连线删掉
- 重复1和2,直到所有的点都被删掉
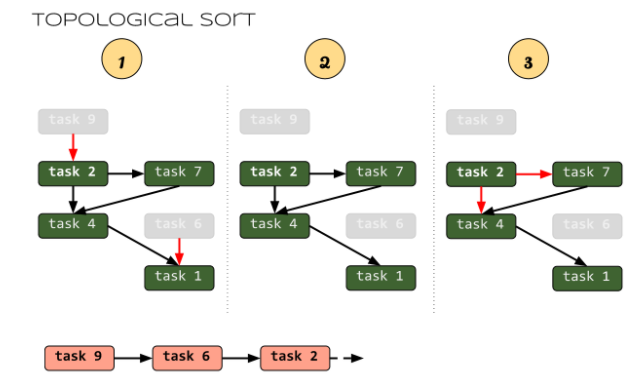
另一种拓扑排序算法
从任意节点开始DFS,并记录每个节点的结束时间。最后将结束时间从大到小排序,得到的结果就是拓扑排序。
这是算法导论上看到的算法。这个算法只适用于有向无环图的拓扑排序,并不能判断是否有环。
例题2,Topological Sorting
实现拓扑排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| 1. 把所有入度为0的点放入队列
2. 将这个队列开始BFS
3. 每拿出一个点:例如拿出1/2/3,每拿一个,要将每个的入度减一
public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph){
ArrayList<DirectedGraphNode> result = new ArrayList<DirectedGraphNode>();
HashMap<DirectedGraphNode, Integer> map = new HashMap<>();
for(DirectedGraphNode node : graph){
for(DirectedGraphNode neibor : node.neighbors){
if(map.containsKey(neibor)) map.put(neibor, map.get(neibor) + 1);
else map.put(neibor, 1);
}
}
Queue<DirectedGraphNode> q = new LinkedList<DirectedGraphNode>();
for(DirectedGraphNode node : graph){
if(!map.containsKey(node)){
q.offer(node);
result.add(node);
}
}
while(!q.isEmpty()){
DirectedGraphNode node = q.poll();
for(DirectedGraphNode neibor : node.neighbors){
q.put(neibor, q.get(neibor) - 1);
if(q.get(neibor) == 0){
result.add(neibor);
queue.offer(neibor);
}
}
}
return result;
}
|
Course Schedule
给n门课,和课之间的先后上课顺序。求这些课能否正常依次上完。
思路:其实就是寻找课程之间有没有环路,如果存在环路,那就不行!
方法1,BFS
一个有向无环图,他一定至少有一个 入度为0的结点,一个出度为0的结点。所以,如果我们从入度入手:
- 先把入度为0的结点删除了。
- 然后再把删除后重新成为入度为0的结点删除了。
- 依次循环,最后,如果,删除的结点个数不等于图总结点个数,那么,就是有环图。
想用BFS,那就肯定得用队列了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| private int[] countIn(int numCourses, int[][] prerequisites){
int[] Incounter = new int[numCourses];
for(int[] edges : prerequisites){
++Incounter[edges[0]];
}
return Incounter;
}
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] InCounter = countIn(numCourses, prerequisites);
Queue<Integer> queue = new LinkedList<>();
for(int i = 0; i < numCourses; ++i){
if(InCounter[i] == 0) queue.add(i);
}
if(queue.isEmpty()) return false;
while (!queue.isEmpty()){
int preCourse = queue.poll();
for(int[] edage : prerequisites){
if(edage[1] != preCourse) continue;
--InCounter[edage[0]];
if(InCounter[edage[0]] == 0){
queue.add(edage[0]);
}
}
}
for(int i : InCounter) if(i != 0) return false;
return true;
}
|
当然了,上面寻找每个点的邻居的方法太暴力了。我们再优化一下。 优化点:
- 记录每个点的邻居
- 在末尾记录入度为0的点的个数!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
class Node{
int inCounter;
List<Integer> neighbors;
Node(){
inCounter = 0;
neighbors = new LinkedList<>();
}
}
private Node[] countIn(int numCourses, int[][] prerequisites){
Node[] Incounter = new Node[numCourses];
for(int i = 0; i < numCourses; ++i) Incounter[i] = new Node();
for(int[] edges : prerequisites){
++Incounter[edges[0]].inCounter;
Incounter[edges[1]].neighbors.add(edges[0]);
}
return Incounter;
}
public boolean canFinish(int numCourses, int[][] prerequisites) {
Node[] InCounter = countIn(numCourses, prerequisites);
int zeroIn = 0;
Queue<Integer> queue = new LinkedList<>();
for(int i = 0; i < numCourses; ++i){
if(InCounter[i].inCounter == 0) {queue.add(i); ++zeroIn;}
}
if(queue.isEmpty()) return false;
while (!queue.isEmpty()){
int preCourse = queue.poll();
List<Integer> neibors = InCounter[preCourse].neighbors;
for(int neibor : neibors) {
--InCounter[neibor].inCounter;
if (InCounter[neibor].inCounter == 0) {
queue.add(neibor);
++zeroIn;
}
}
}
return zeroIn == numCourses;
}
|
方法2,DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Node{
List<Integer> neibors = new LinkedList<>();
}
private Node[] shift(int numCourses, int[][] prerequisites){
Node[] nodes = new Node[numCourses];
for(int i = 0; i < numCourses; ++i) nodes[i] = new Node();
for(int[] edge : prerequisites){
nodes[edge[1]].neibors.add(edge[0]);
}
return nodes;
}
boolean[] used;
private boolean dfs(Node[] nodes, int idx, boolean[] visited){
if(visited[idx]) return false;
visited[idx] = true;
for(int neibor : nodes[idx].neibors){
if(!dfs(nodes, neibor, visited)) return false;
}
visited[idx] = false;
used[idx] = true;
return true;
}
public boolean canFinish(int numCourses, int[][] prerequisites) {
Node[] nodes = shift(numCourses, prerequisites);
boolean[] visited = new boolean[numCourses];
used = new boolean[numCourses];
for(int i = 0; i < numCourses; ++i){
if(used[i]) continue;
if(!dfs(nodes, i, visited)) return false;
}
return true;
}
|
Course Schedule II
给一些课程关系。输出一个合理的上课顺序
方法1,BFS
一样的套路哇
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class Node{
List<Integer> neighbors = new LinkedList<>();
int degrees;
}
private Node[] helper(int numCourses, int[][] prerequisites){
Node[] nodes = new Node[numCourses];
for(int i = 0; i < numCourses; ++i) nodes[i] = new Node();
for(int[] edge : prerequisites){
++nodes[edge[0]].degrees;
nodes[edge[1]].neighbors.add(edge[0]);
}
return nodes;
}
public int[] findOrder(int numCourses, int[][] prerequisites) {
Node[] nodes = helper(numCourses, prerequisites);
Queue<Integer> zeroDegrees = new LinkedList<>();
int zeroCounter = 0;
int[] order = new int[numCourses];
int filled = 0;
for(int i = 0; i < numCourses; ++i){
if(nodes[i].degrees == 0){
order[filled++] = i;
zeroDegrees.add(i);
++zeroCounter;
}
}
while (!zeroDegrees.isEmpty()){
int originIdx = zeroDegrees.poll();
for(int destIdx : nodes[originIdx].neighbors){
--nodes[destIdx].degrees;
if(nodes[destIdx].degrees == 0){
order[filled++] = destIdx;
zeroDegrees.add(destIdx);
++zeroCounter;
}
}
}
if(zeroCounter == numCourses) return order;
else return new int[0];
}
|
DFS
Evaluate Division
先给一些算式,例如a / b = 2.0, b / c = 3.0。求a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
思路:将每个符号看成图中的一个点,把运算看做可达关系。如果某两点可达,这说明这两点之间可以算出一个值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| private double dfs(String original, String curr, HashSet<String> visited){
if(!nodes.containsKey(curr) || !nodes.containsKey(original)) return -1;
if(nodes.get(original).containsKey(curr)) return nodes.get(original).get(curr);
HashMap<String,Double> original_neighbors = nodes.get(original);
for(Map.Entry<String, Double> entry : original_neighbors.entrySet()){
if(visited.contains(entry.getKey())) continue;
visited.add(entry.getKey());
double nextResult = dfs(entry.getKey(), curr, visited);
if(nextResult > 0) return nextResult * entry.getValue();
visited.remove(entry.getKey());
}
return -1.0;
}
HashMap<String, HashMap<String, Double>> nodes;
public double[] calcEquation(String[][] equations, double[] values, String[][] queries) {
nodes = new HashMap<>();
for(int i = 0; i < equations.length; ++i){
for(int k = 0; k < 2; ++k) {
if (!nodes.containsKey(equations[i][k])) {
nodes.put(equations[i][k], new HashMap<>());
}
}
nodes.get(equations[i][0]).put(equations[i][1], values[i]);
nodes.get(equations[i][1]).put(equations[i][0], 1/values[i]);
}
double[] result = new double[queries.length];
HashSet<String> visited = new HashSet<String>();
for(int i = 0; i < queries.length; ++i){
visited = new HashSet<String>();
visited.add(queries[i][0]);
result[i] = dfs(queries[i][0], queries[i][1], visited);
if(nodes.containsKey(queries[i][0]) && nodes.containsKey(queries[i][1])){
nodes.get(queries[i][0]).put(queries[i][1], result[i]);
nodes.get(queries[i][1]).put(queries[i][0], 1/result[i]);
}
visited.remove(queries[i][0]);
}
return result;
}
|
BFS
Minimum Genetic Mutation
基因由长度为8的字符表示。基因突变指改变某一个位置使得它变成bank中的某个基因。给出如下
1
2
3
| start: "AACCGGTT"
end: "AACCGGTA"
bank: ["AACCGGTA"]
|
假设每次突变后必须成为bank中的一个。求start到end的最少突变次数。
思路:其实这是个图的问题。将每个基因看成图中的一个点,点之间的距离就是两个字符串的汉明距离。如果汉民距离大于1,那么距离无效。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
int maxValue = 100;
public int minMutation(String start, String end, String[] bank) {
int n = bank.length + 2;
int[][] dist = new int[n][n];
boolean ifIn = false;
for(int i = 0; i < bank.length; ++i){
dist[0][i+1] = distComputer(start, bank[i]);
dist[i+1][0] = dist[0][i+1];
dist[n-1][i+1] = distComputer(end, bank[i]);
dist[i+1][n-1] = dist[n-1][i+1];
if(dist[n-1][i+1] == 0) ifIn = true;
}
if(!ifIn) return -1;
for(int i = 0; i < bank.length; ++i){
for(int j = i + 1; j < bank.length; ++j){
dist[i+1][j+1] = distComputer(bank[i], bank[j]);
dist[j+1][i+1] = dist[i+1][j+1];
}
}
dist[0][n-1] = maxValue;
dist[n-1][0] = maxValue;
int[] dp = new int[n];
Arrays.fill(dp, maxValue);
dp[n-1] = 0;
Queue<Integer> queue = new LinkedList<>();
queue.offer(n-1);
while (!queue.isEmpty()){
int size = queue.size();
while (size > 0){
int from = queue.poll();
for(int to = 0; to < n; ++to){
if(dist[from][to] > 1 || dp[to] < maxValue) continue;
dp[to] = dp[from] + dist[from][to];
queue.offer(to);
}
--size;
}
}
return dp[0] == maxValue ? -1 : dp[0];
}
private int distComputer(String a, String b){
int d = 0;
for(int i = 0; i < a.length(); ++i){
if(a.charAt(i) != b.charAt(i)) ++d;
}
return d;
}
|

