经典扫描线

经典问题：数飞机问题

给一些飞机飞行的时间区间。求天上最多有多少个飞机同时在飞。

例如给

[1,3]
[2,4]
[5,6]

求天上同时有多少架飞机

思路一，细粒度扫描

遍历每个时刻粒度，检测每个时刻有多少个飞机

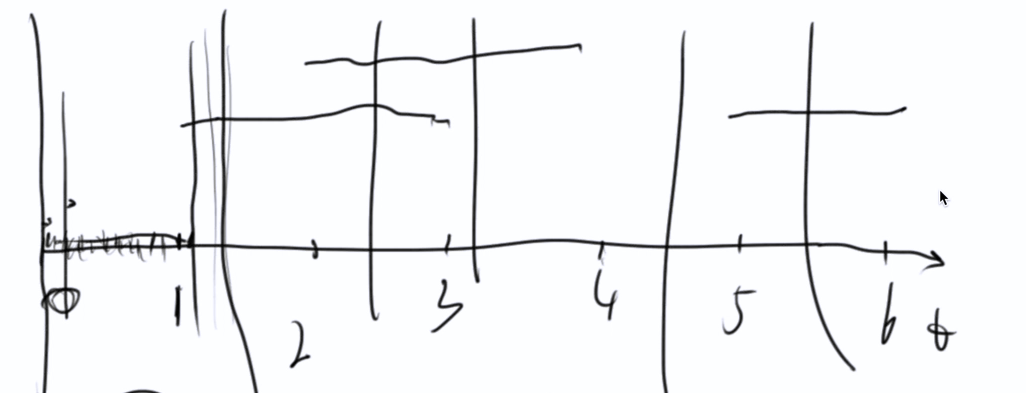
思路二，扫描线！

不需要检测每一时刻，只需要检测起点或者终点的位置！（交点变化的位置只有起点或者终点）

将数据拆成二元组 [起点/终点标识，时刻]
按照时刻排序
依次扫描

/**
 * Definition of Interval:
 * public classs Interval {
 *     int flag, end;
 *     Interval(int flag, int end) {
 *         this.flag = flag;
 *         this.end = end;
 *     }
 */

class Point{
  int time;
  int flag; // 1=start, 0=end
  Point(int time, boolean flag){
    this.time = time;
    this.flag = flag;
  }
  public static Comparator<Point> pointComparator = new Comparator<Point>(){
    public int compare(Point p1, Point p2){
      if(p1.time == p2.time) return p1.flag - p2.flag; // 如果时间一致，如果两个都是start或都是end，那么它两相等。如果p1是start而p2是end，那么p1 > p2
      else return p1.time - p2.time;
    }
  }
  
  public int countOfAirplanes(List<Interval> airplanes){
    List<Point> list = new ArrayList<>(airplanes.size()*2);
    for(Interval i : airplanes){
      list.add(new Point(i.start, 1));
      list.add(new Point(i.end, 0));
    }
    Collections.sort(list, Point.PointComparator);
    int count = 0, ans = 0;
    for(Point p : lists){
      // 遇到起点就+1
      if(p.flag == 1) ++count;
      // 遇到终点就-1
      else --count;
      ans = Math.max(ans, count);
    }
  }
}

相关题：meeting rooms。有会议时间安排表。求问多少个会议室能完成这些会议。

扫描线+堆

Building Outline

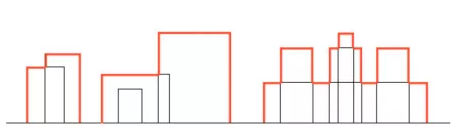
已知每个楼房的[start, end, height]。例如

[
  [1, 3, 3],
  [2, 4, 4],
  [5, 6, 1]
]

求楼房的轮廓：

[
  [1, 2, 3],
  [2, 4, 4],
  [5, 6, 1]
]

思路一，扫描线

一个刻度一个刻度扫描，得到每个刻度下的高度。

思路二，优化扫描线

只需要扫描起点或终点的高度。

例如将上数据变为

[1, T, 3]  T代表是开头，F代表结尾
[3, F, 3]
[2, T, 4]
[4, F, 4]
[5, T, 1]
[6, F, 1]

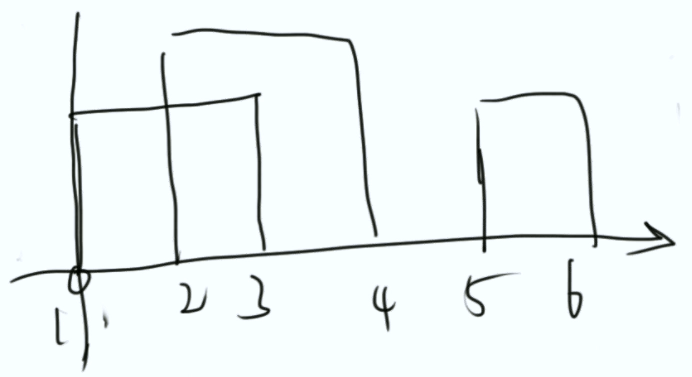
扫描到当前时，需要用到当前的最大值！因此可以引入堆！

在堆上维护当前的最大值，到end时，将这个元素去除。

这个过程可以看https://briangordon.github.io/2014/08/the-skyline-problem.html这里的一个动图

彩色的部分表示堆里的元素，堆里面放的是当前的有效高度

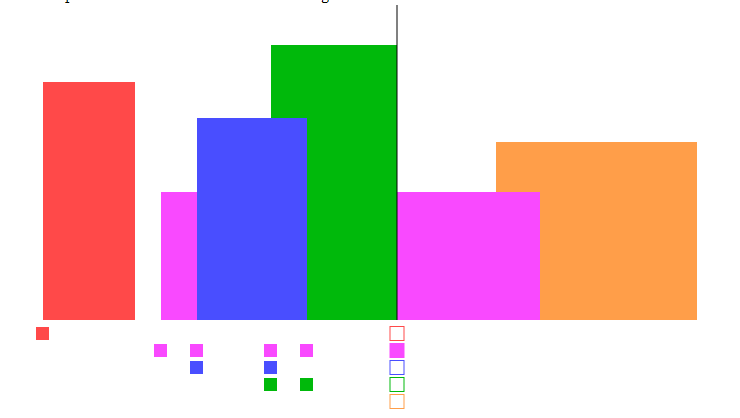
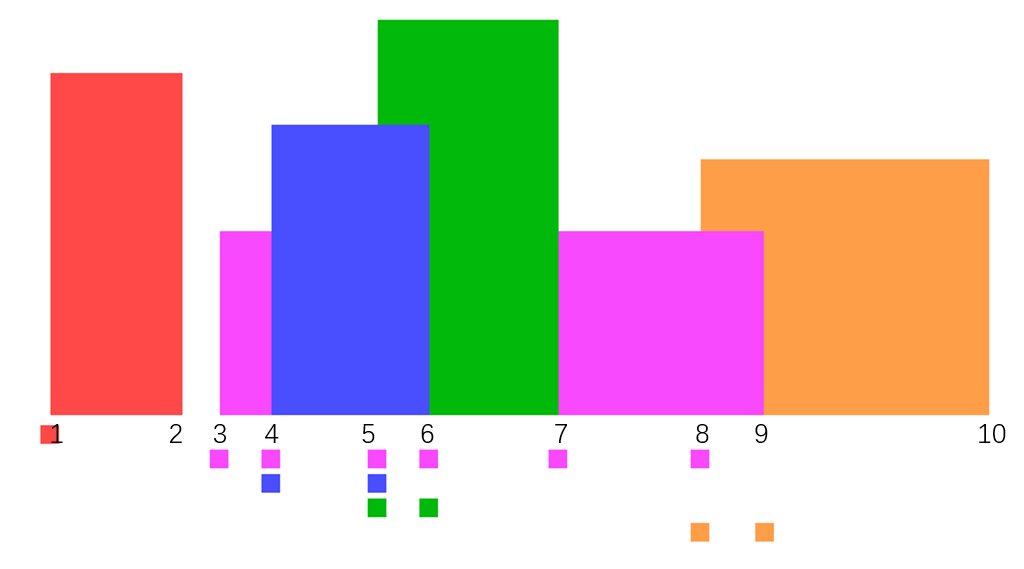
如上图所示，标注的10个点是起点或终点。

将10个点按照x排序。如果某个点的x坐标一致，那就终点优先。
依次放入堆中：
1. 当扫描到1时，1是起点，且堆为空。那么1一定是突变点（从0到有）。点[1, height] 进入候选中心。且点1的高度入堆。
2. 扫描到2时，2是终点，那么就先把2对应的起点delete掉。此时堆为空，那么2一定是突变点(从有到0)，点[2, height = 0] 进入候选中心
3. 扫描到3时，3是起点，且堆为空。那么3是突变点（从0到3）。点[3,height]进入候选中心。且点3的高度入堆。
4. 扫描到4时，4是起点，且堆不为空，且4的高度大于当前堆的最大值，那么4是突变点。点[4,height]进入候选中心。且点4的高度入堆。
5. 扫描到5时，5是起点，且堆不为空，且5的高度大于当前堆的最大值，那么5是突变点。点[5,height]进入候选中心，且点5的高度入堆。
6. 扫描到6时，6是终点，那么就先把6对应的起点4delete掉。且发现6的高度小于当前堆的最大值，那么6不是突变点。继续
7. 扫描到7时，7是终点，先把7对应的起点5delete掉。发现7的高度大于当前堆的最大值，那么7是突变点，点[7,height]进入候选中心。
8. 扫描到8....9....10

甲乙小朋友的房子

算法-扫描线

经典扫描线

扫描线+堆