素数
判断n是素数
解法一,暴解
如果n是素数,那么n不能被任何数(1和n除外)的数字整除。暴力的方法就是从2~n-1进行探测,探测\(\frac{n}{k}, k = 2,3,...,n-1\) 是否是整数
1 | private boolean ifPrime(int n){ |
解法二,优化
事实上,如果n不是素数,那么一定存在\(n = a \times b\) ,而a和b的可能性有:
| a | b |
|---|---|
| 2 | n/2 |
| 3 | n/3 |
| ... | ... |
| n/3 | 3 |
| n/2 | 2 |
我们发现,a和b有重复计算的部分,即如果a < sqrt(n) , 那么b > sqrt(n) 。因此a只用探测到sqrt(n)即可。
1 | private boolean ifPrime(int n){ |
解法三,素数筛——生成素数序列:埃拉托斯特尼筛法
素数筛能非常高效地生成素数序列。原理是剔除所有可被素数整除的非素数。
- 列出2~max所有的数字
- 剔除所有2的倍数(2保留)
- 剔除下一个没有被划掉的倍数
- 循环直到max
1 | public int countPrimes(int n) { |
面积问题
Perfect Rectangle
假设一个矩形有四个数表示[a,b,c,d] 。其中[a,b] 代表left bottom角的坐标,[c,d] 表示right top的坐标。给一堆矩形,判断它是否能刚刚好(不重合也不漏缺)地构成一个大的矩形
这道题耗费了较长时间。因为没想通。
核心思想就是:能够正好围成一个矩形的情况就是: 有且只有:
- 最左下 最左上 最右下 最右上 的四个点只出现过一次,其他肯定是成对出现的(保证完全覆盖)
- 上面四个点围成的面积,正好等于所有子矩形的面积之和(保证不重复)
1 | class Pair{ |
Perfect Number
定义完美数字为:除了它自己以外的所有除数相加都等于它本身。判断一个数是不是一个完美数字。
与上面的类似解法
1 | public boolean checkPerfectNumber(int num) { |
组合数学
环形染色问题
如果把一个圆环分成n个区域\(A_n\)。用m种不同颜色为这n个区域染色。要求相邻两个区域\(A_i\) 和 \(A_{i+1}\) 颜色不同,则不同的染色方式有多少种?

- 对于区域\(A_1\) ,有m种染色法;
- 对于区域\(A_2,...,A_{n-1}\) ,分别有m-1种染色法
- 假设暂时不考虑\(A_n\) 与\(A_1\) ,那么对于区域\(A_n\) ,有\(m-1\) 种染法。
- 如果\(A_n\) 与\(A_1\) 同色,那么就将这两个看成同一个区域,这就退化成了n-1个区域的染色种类,即\(a_{n-1}\)
- 因此有\[a_n + a_{n-1} = m(m-1)^{n-1}\]
接下来通过数列递推公式求通项公式:
由于对上式两边同时减去\((m-1)^n\):
\[a_n + a_{n-1} - (m-1)^n = m(m-1)^{n-1} - (m-1)^n\] ,递推可得:
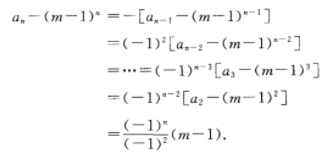
因此,环形染色问题的解为:
\[a_n = (m-1)^n + (-1)^n(m-1)\]
计算几何
Valid Square
验证给定的四个点是否能组成正方形。
1 | class Solution { |