出栈顺序问题
今天看到一道出栈顺序的面试题,很心的思路。特来注意一下。
问题定义
一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
解题思路
- 假设进栈序列为\([a,b,c,d]\) . 设\(f(k)\) 表示还剩k个元素时的出栈序列数目(元素内容并不影响数目,例如abc与abd的出栈序列数目是一样的)
- 如果a第1个出栈,那么只有可能就是a进栈后马上出栈。还剩bcd等待操作。那么就是子问题\(f(3)\)
- 如果a第2个出栈,那么一定有一个元素先比a进栈,这个元素只可能是b。那么就是子问题\(f(1)\)。 而还剩下cd等待操作,那么cd就是子问题\(f(2)\)
- 如果a第3个出栈,那么一定有2个元素比a先出栈,这2个元素只可能是bc,就是子问题\(f(2)\) 。而剩下的d就是\(f(1)\)
- 如果a第4个出栈,那么一定是a进栈后,等到bcd都出栈后再出栈。那么bcd就是\(f(3)\)
结合以上所有情况,即\(f(4) = f(3) + f(2)\times f(1) + f(1) \times f(2) + f(3)\)
为了好看,我们定义\(f(0) = 1\) ,然后推广到n,那么可以得到:
\[f(n) =f(0)\times f(n) + f(1)\times f(n-1) +...+f(k)(n-k)+...+ f(n-1) \times f(1) + f(n) \times f(0)\]
\[ = \sum_{i=0}^{n-1} f(i)f(n-i)\]
卡兰特数
再探出栈顺序问题
首先,每一种进出栈的顺序都与出栈序列一一对应.也就是说,如果我们用+1表示进栈,−1表示出栈,那么1234的一个出栈序列1342与进出栈顺序
\[+1,+1,−1,+1,+1,−1,−1,−1\]
是对应的。
那么对n个数字的序列,总的进出站序列是给2n个1前面挑n个+号,其它的-号,共\(C_{2n}^n\) 种吗?
答案是否定的,因为出栈的前提要有进栈动作。于是要求每个排列中的若干前项和均不为负数。也就是说排列:
\[1,−1,−1,1,1,−1,−1,1\]
是无效的。
那么无效的排列究竟有多少种呢?
假设M是所有无效的排列构成的集合。考虑其中第一次发现排列无效时,也就是第一次发现前若干项和为-1时,此时我们将包含使得前若干项和为-1的这一项开始的之前所有项全部都取相反数。那么就会得到一个新的排列,这个排列包含\(n+1\) 个\(+1\) , \(n - 1\) 个 \(-1\) 。设所有这样的排列构成集合N。
显然这个\(M -> N\) 的映射是一一映射。\(N\) 中的每一个排列从第一项往后累积求和的时候必然会出现和为+1的情形,此时将排列中使得和为+1的这一项连同之前的所有项全部取相反数,那么就会得到M中的一个排列)
因此无效排列共有\({\rm C}_{2n}^{n-1}\) 个。
综上,所有不同的出栈序列总数为\({\rm C}_{2n}^n-{\rm C}_{2n}^{n-1}\) ,即
\[C_n = \dfrac 1{n+1}{\rm C}_{2n}^n\]
二叉树问题
进出栈问题的一个简单变形就是二叉树问题:求n个叶子的二叉树的个数
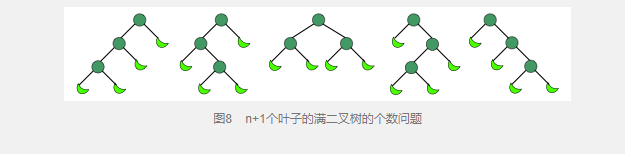
图上有3个叶子节点,其中圆形表示节点,月牙表示空。一共有5种方案。
朴素法
假设\(f(k)\) 表示k个节点的二叉树数目,那么根节点消耗掉1个,左边i个,右边就是n-i-1个
\(f(n) = \sum_{i=0}^{n-1} f(i)f(n-i-1)\)
如果直接计算,就会消耗\(O(n^2)\) 的时间。
转化问题
如果我们按照深度优先遍历二叉树,向下遍历代表入栈,用+1表示,向上回溯代表出栈,用-1表示。那么第一个图记为:
\[+1, +1, +1, -1, -1, -1\]
这样,将每一种不同的二叉树都对应到了一种不同的排列序列,同样对于每一种不同的排列序列都可以找到对应的一种不同的二叉树,因此,有n 个结点的二叉树的数量也是 \(C_n\) (上面的卡兰特数)
变种:2n+1个节点的满二叉树有多少种?
满二叉树代表一个节点要么有两个孩子,要么没有孩子。其实与上一题一样的,将上一题的月牙变换成叶子就可以了。
2n+1个节点组成的不同构满二叉树的方案数为\(C_n\) 个
括号序列计数
再来看一个问题:有多少种不同的 n 对合法括号序列?
括号其实与上面的正负一都一样。左括号代表入栈,右括号代表出栈。n对括号代表入栈n次,出栈n次。那么不同的出栈序列一共有\(C_n\) 种
电影购票
电影票每张50元,如果有m+n个人排队买票,其中m个人各持有50元面值的钞票1张,另外n个人各持有100元面值的钞票1张,而票房没有预备找零.有多少种方法可以将这m+n个人排成一列,顺序购票,使得无需因为等待找零而耽误时间?
我们记持有50元的人叫A,记持有100元的人叫B。那么只要当前已购票的人中,A的个数大于B的个数即可。我们记A购票为入栈,B购票为出栈。那么这个问题就转化成了之前的问题。假设m==n,那么不同的出栈序列一共有\(C_n\) 种
图形化解释
利用这个模型,我们解释进出栈问题的几何解释。
对于持有100元的n个人A来说,我们可以做以下图形标记:

假设50元人购票记为向右走;100元人购票向上走。那么我们只需要保证当前点不要超过\(y=x\) 这条对角线即可!
卡兰特数的证明
如图3,在一个\(m×n\)的网格中,从左下角的原点\(O(0,0)\)出发,每次向右(表示接待的观众持有50元的钞票)或向上(表示接待的观众持有100元的钞票)移动,最终到达\(P(m,n)\).我们需要找到在直线\(y=x\)下方(包括边界)的路径条数.
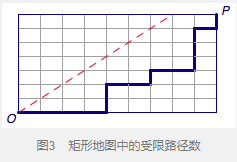
从反面考虑问题.设M为穿过直线\(y=x\)(表示会经过直线上方的点)的从\(O→P\)的路径组成的集合,如图4.

如图5,利用对称可以将M中第一次犯规时的路径对称,然后再将剩下的部分接在对称后的路径上,由于此时将一次向上移动修改为了向右移动,因此终点由P变成了P′,此时就建立了与O到P′的路径的一个一一映射.
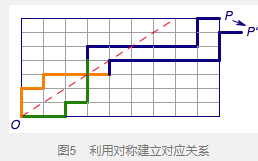
因此
\[{\rm{card}}(M)= {\rm{card}}(N)={\rm{C}}_{m + n}^{n-1}\]
于是所求的排列数为
\[{\rm{C}}_{m + n}^n-{\rm{C}}_{m + n}^{n-1}\]
特别地,当\(m = n\) 时,有
\[{\rm{C}}_{m + n}^n-{\rm{C}}_{m + n}^{n-1} = {\rm{C}}_{2n}^n-{\rm{C}}_{2n}^{n-1} = \dfrac{1}NaN{\rm{C}}_{2n}^n\]
即卡兰特数