再不学深度学习,就真的跟不上了。
梯度下降法的改进
原始梯度下降
设\(f(\mathbf x ^{(i)}, \theta)\)是神经网络,一共有m个样本。在第t次迭代(epoch)时,用m个训练样本\(\{\mathbf x^{(i)}, y^{(i)} \}_{i=1}^m\),分别用每个样本分别计算每个维度上的梯度,然后将m个梯度加起来: \[\mathbf g_t = \frac{1}{m} \sum_{i \in I_t} \frac {\partial J(y^{(i)}, f(\mathbf x ^{(i)}, \theta))}{\partial \theta}+ \lambda \|\theta\| ^2\]
算好梯度后就可以更新参数了: \[\theta_t = \theta_{t-1} - \alpha \mathbf g_t\] \[\theta_t = \theta_{t-1}+ \Delta \theta_t\]
Mini-Batch Gradient Descent
对整个训练集进行梯度下降法的时候,我们必须处理整个训练数据集,然后才能进行一步梯度下降,即每一步梯度下降法需要对整个训练集进行一次处理,如果训练数据集很大的时候,如有500万或5000万的训练数据,处理速度就会比较慢。
但是如果每次处理训练数据的一部分,即用其子集进行梯度下降,则我们的算法速度会执行的更快。而处理的这些一小部分训练子集即称为Mini-batch。
将样本分成k个mini-batch,每个mini-batch包含[m/k]个样本;在每个mini-batch里计算每个样本的梯度,然后在这个mini-batch里求和取平均作为最终的梯度来更新参数;然后再用下一个mini-batch来计算梯度,如此循环下去直到k个mini-batch操作完就称为一个epoch结束。
Momentum(动量梯度下降)
比标准的 gradient descent 要快,基本想法是,计算梯度的 指数加权平均数(exponentially weighted average of gradients),并利用该梯度更新权重。
首先定义指数加权平均: \[v_t=\beta v_{t-1}+(1-\beta)\theta_t\]
在我们优化 Cost function 的时候,以下图所示的函数图为例:
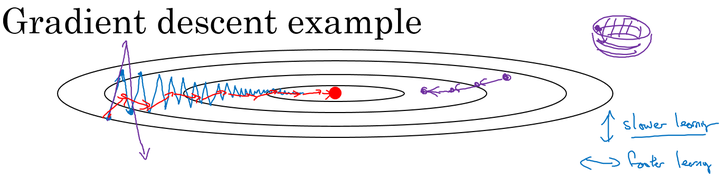
在利用梯度下降法来最小化该函数的时候,每一次迭代所更新的代价函数值如图中蓝色线所示在上下波动,而这种幅度比较大波动,减缓了梯度下降的速度,而且我们只能使用一个较小的学习率来进行迭代。
如果用较大的学习率,结果可能会如紫色线一样偏离函数的范围,所以为了避免这种情况,只能用较小的学习率。
但是我们又希望在如图的纵轴方向梯度下降的缓慢一些,不要有如此大的上下波动,在横轴方向梯度下降的快速一些,使得能够更快的到达最小值点,而这里用动量梯度下降法既可以实现,如红色线所示。
实现方法(以W为例,b同理):
\[v_{dw}=\beta v_{dw}+(1-\beta)dW\] \[W=W-\alpha v_{dw}\]
在对应上面的计算公式中,将Cost function想象为一个碗状,想象从顶部往下滚球,其中:
- 微分项\(dW\) 想象为球提供的加速度;
- 动量项\(v_{dw}\)相当于速度;
小球在向下滚动的过程中,因为加速度的存在使得速度会变快,但是由于 的存在,其值小于1,可以认为是摩擦力,所以球不会无限加速下去。
AdaGrad
每次迭代时,根据历史梯度累积量来减少学习率,减小梯度。即: \[V_t=\sum_{i=1}^tv_i^2\]
\[W=W-\frac{\alpha}{\sqrt{G_t+\epsilon}} v_{dw}\]
优点:也就是说,前期Vt较小,能够放大梯度;而后期Vt比较大,能够约束梯度;
缺点:迭代次数过多时,学习率会非常小,会过早停止训练;
RMSprop
除了上面所说的Momentum梯度下降法,RMSprop(root mean square prop)也是一种可以加快梯度下降的算法。
计算梯度平方的指数递减移动平均, 即梯度平方的平均值来减小梯度。 \[S_{dw}=\beta S_{dw}+(1-\beta)dw^2\] \[W=W-\alpha \frac{dw}{\sqrt{S_{dw}+\epsilon}}\]
优点:
- 解决了AdaGrad学习率一直递减过早停止训练的问题,学习率可大可小
- 训练初中期,加速效果不错,很快;训练后期,反复在局部最小值抖动
- 适合处理非平稳目标,对于RNN效果很好
缺点:
- 依然依赖于全局学习率α0
Adam
Adam (Adaptive Moment Estimation)优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法。
Adam[6] 可以认为是 RMSprop 和 Momentum 的结合。和 RMSprop 对二阶动量使用指数移动平均类似,Adam 中对一阶动量也是用指数移动平均计算。
其中,初值
注意到,在迭代初始阶段, 和
有一个向初值的偏移(过多的偏向了 0)。因此,可以对一阶和二阶动量做偏置校正 (bias correction),
再进行更新,
可以保证迭代较为平稳。
