基本概览
概率主题模型:隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA)。
按照wiki上的介绍,LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出,是一种主题模型,它可以将文档集中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。
LDA模型有一个前提,就是一篇文档生成的方式(注意是文档哦)如下:
- 从狄利克雷分布\(\alpha\)中取样生成文档i的主题分布\(\theta_i\)
- 从文档i的主题分布\(\theta_i\)中取样生成文档i第j个词的主题\(z_{i,j}\)
- 从狄利克雷分布\(\beta\)中取样生成主题\(z_{i,j}\)对应的词语分布\(\phi_{z_{i,j}}\)
- 从词语的多项式分布\(\phi_{z_{i,j}}\)中采样最终生成词语\(w_{i,j}\)
其中,类似Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布。
此外,LDA的图模型结构如下图所示(类似贝叶斯网络结构):
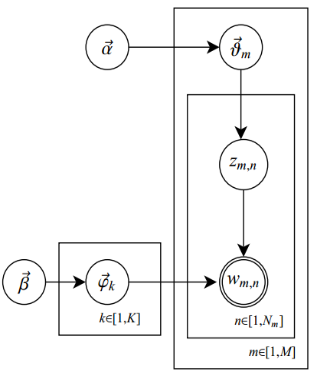
知道理解LDA,可以分为下述5个步骤:
- 一个函数:gamma函数
- 四个分布:二项分布、多项分布、beta分布、Dirichlet分布
- 一个概念和一个理念:共轭先验和贝叶斯框架
- 两个模型:pLSA、LDA
- 一个采样:Gibbs采样
本文便按照上述5个步骤来阐述。
几个分布
二项分布
二项分布是从伯努利分布推进的。伯努利分布,又称两点分布或0-1分布,是一个离散型的随机分布,其中的随机变量只有两类取值,非正即负{+,-}。而二项分布即重复n次的伯努利试验,记为\(X\text{~}b(n,p)\)。简言之,只做一次实验,是伯努利分布,重复做了n次,是二项分布。二项分布的概率密度函数为:
\[P(K=k)= \begin{pmatrix} n \\ k \\ \end{pmatrix} p^k(1-p)^{n-k} \]
对于k=0,1,2,....,n,其中的$ \[\begin{pmatrix} n \\ k \\ \end{pmatrix}\]=\(是二项式系数,又记作\)C(n,k)$。
多项分布
多项分布,是二项分布扩展到多维的情况
多项分布是指单次试验中的随机变量的取值不再是0-1的,而是有多种离散值可能(1,2,3...,k)。比如投掷6个面的骰子实验,N次实验结果服从K=6的多项分布。其中
\[\sum_{i=1}^kp_i=1, p_i > 0\]
多项分布的概率密度函数为:
\[P(x_1,x_2,...,x_k;p_1,p_2,...,p_k)=\frac{n!}{x_1!...x_k!}p_1^{x^1}...p_k^{x_k}\]
Beta分布
Beta分布是二项分布的共轭先验分布
给定参数\(\alpha>0, \beta > 0\),取值范围为[0,1]的随机变量x的概率密度函数:
\[f(x;\alpha, \beta)=\frac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta-1}\]
其中,
\[\frac{1}{B(\alpha,\beta)}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}, \Gamma(z)=\int_0^{\infty} {t^{-1}e^{-t}} \,{\rm d}t \]
其中,\(\Gamma(x)\)是gamma函数。
Dirichlet分布
Dirichlet分布,是beta分布在高维度上的推广
Dirichlet分布的的密度函数形式跟beta分布的密度函数如出一辙 :
\[{\displaystyle f(x_{1},\dots ,x_{K};\alpha _{1},\dots ,\alpha _{K})={\frac {1}{\mathrm {B} (\alpha )}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1}}\]
其中,\({\mathrm {B}}(\alpha )={\frac {\prod _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma {\bigl (}\sum _{i=1}^{K}\alpha _{i}{\bigr )}}},\qquad \alpha =(\alpha _{1},\dots ,\alpha _{K}).\)
至此,我们可以看二项分布和多项分布很相似,Beta分布和Dirichlet 分布很相似,而至于“Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布”。
总结
我们知道beta分布是二项式分布的共轭先验概率分布。对于非负实数\(\alpha,\beta\),我们有如下关系:
\[Beta(p|\alpha,\beta)=Count(m_1,m_2)=Beta(p|\alpha+m_1, \beta+m_2)\]
其中\((m_1,m_2)\)对应的是二项分布\(B(m_1+m_2,p)\)的计数。针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial 共轭。
我们知道狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布,把\(\alpha\)从整数集合拓展到实数集合,从而得到更一般的表达式:
\[Dir(\vec{p}|\vec{\alpha})=MultCount(\vec{m})=Beta(p|\vec{\alpha}+\vec{m})\]
针对于这种观测到的数据符合多项分布,参数的先验分布和后验分布都是Dirichlet 分布的情况,就是 Dirichlet-Multinomial 共轭。
主题模型LDA
在杀到终极boss——LDA模型之前,再循序渐进理解基础模型:Unigram model、mixture of unigrams model,以及跟LDA最为接近的pLSA模型。为了方便描述,首先定义一些变量:
- \(w\)表示词,\(V\)表示所有单词个数
- \(z\)表示主题,\(k\)是主题个数
- \(D=(w_1,...,w_M)\)表示语料库,M是文档数目
- \(w=(w_1,...,w_N)\)表示文档,N是文档中的词数
Unigram model
对于文档\(w=(w_1,...,w_N)\),用\(p(w_n)\)表示词\(w_n\)的先验概率,生成文档w的概率为:
\[p(w)=\prod_{n=1}^Np(w_n)\]
其图模型为:
图中被涂色的w表示可观测变量,N表示一篇文档中总共N个单词,M表示M篇文档

或为:

unigram model假设文本中的词服从Multinomial分布,而我们已经知道Multinomial分布的先验分布为Dirichlet分布。
上图中的\(w_n\)表示在文本中观察到的第n个词,\(n\in[1,N]\)表示该文本中一共有N个单词。加上方框表示重复,即一共有N个这样的随机变量\(w_n\)。其中,p和\(\alpha\)是隐含未知变量。
- p是词服从的Multinomial分布的参数
- α是Dirichlet分布(即Multinomial分布的先验分布)的参数。
一般α由经验事先给定,p由观察到的文本中出现的词学习得到,表示文本中出现每个词的概率。
PLSA模型
因为跟LDA模型最为接近的便是下面要阐述的这个pLSA模型,理解了pLSA模型后,到LDA模型也就一步之遥——给pLSA加上贝叶斯框架,便是LDA。
根据主题词生成文档
实际中,一篇文章往往有多个主题,只是这多个主题各自在文档中出现的概率大小不一样。比如介绍一个国家的文档中,往往会分别从教育、经济、交通等多个主题进行介绍。那么在pLSA中,文档是怎样被生成的呢?
假设你要写M篇文档,由于一篇文档由各个不同的词组成,所以你需要确定每篇文档里每个位置上的词。
再假定你一共有K个可选的主题,有V个可选的词。一般来说,选主题和选词都是两个随机的过程,先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后从该主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。 最后,你不停的重复扔“文档-主题”骰子和”主题-词项“骰子,重复N次(产生N个词),完成一篇文档,重复这产生一篇文档的方法M次,则完成M篇文档。

上述过程抽象出来即是PLSA的文档生成模型。在这个过程中,我们并未关注词和词之间的出现顺序,所以pLSA是一种词袋方法。具体说来,该模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别\(z_k\in{z_1,...,z_K}\)。同时定义:
- \(P(d_i)\)表示海量文档中某篇文档被选中的概率;
- \(P(w_j|d_i)\)表示词\(w_j\)在给定文档\(d_i\)中出现的概率;
- \(P(z_k|d_i)\)表示具体某个主题\(z_k\)在给定文档\(d_i\)下出现的概率
- \(P(w_j|z_k)\)表示具体某个词\(w_j\)在给定主题\(z_k\)下出现的概率。与主题关系越密切的词,其条件概率越大。
利用上述的第1、3、4个概率,我们便可以按照如下的步骤得到“文档-词项”的生成模型:
- 按照概率\(P(d_i)\)选择一篇文档\(d_i\)
- 选定文档\(d_i\)后,从主题分布中按照概率\(P(z_k|d_i)\)选择一个隐含的主题类别\(z_k\)
- 选定\(z_k\)后,从词分布中按照概率\(P(w_j|z_k)\)选一个词\(w_j\)
所以pLSA中生成文档的整个过程便是选定文档生成主题,确定主题生成词。
根据文档反推主题分布
反过来,既然文档已经产生,那么如何根据已经产生好的文档反推其主题呢?这个利用看到的文档推断其隐藏的主题(分布)的过程(其实也就是产生文档的逆过程),便是主题建模的目的:自动地发现文档集中的主题(分布)。
换言之,人类根据文档生成模型写成了各类文章,然后丢给了计算机,相当于计算机看到的是一篇篇已经写好的文章。现在计算机需要根据一篇篇文章中看到的一系列词归纳出当篇文章的主题,进而得出各个主题各自不同的出现概率:主题分布。即文档d和单词w是可被观察到的,但主题z却是隐藏的。
如下图所示(图中被涂色的d、w表示可观测变量,未被涂色的z表示未知的隐变量,N表示一篇文档中总共N个单词,M表示M篇文档):

上图中,文档d和词w是我们得到的样本(样本随机,参数虽未知但固定,所以pLSA属于频率派思想。区别于下文要介绍的LDA中:样本固定,参数未知但不固定,是个随机变量,服从一定的分布,所以LDA属于贝叶斯派思想),可观测得到,所以对于任意一篇文档,其\(P(z_k|d_i)\)是已知的。
从而可以根据大量已知的文档-词项信息 \(P(w_j|d_i)\)训练出文档-主题和\(P(z_k|d_i)\)主题-词项,如\(P(w_j|z_k)\)下公式所示:
\[P(w_j|d_i)=\sum_{k=1}^KP(w_j|z_k)P(z_k|d_i)\]
故得到文档中每个词的生成概率为:
\[P(d_i,w_j)=P(d_i)P(w_j|d_i)=P(d_i)\sum_{k=1}^KP(w_j|z_k)P(z_k|d_i)\]
由于\(P(d_i)\)可事先计算求出,而\(P(w_j|z_k)\)和\(P(z_k|d_i)\)未知,所以\(\theta=(P(w_j|z_k),P(z_k|d_i))\)就是我们要估计的参数。
用什么方法进行估计呢,常用的参数估计方法有极大似然估计MLE、最大后验证估计MAP、贝叶斯估计等等。因为该待估计的参数中含有隐变量z,所以我们可以考虑EM算法。
。。。来日填补EM
LDA模型
事实上,理解了pLSA模型,也就差不多快理解了LDA模型,因为LDA就是在pLSA的基础上加层贝叶斯框架,即LDA就是pLSA的贝叶斯版本(正因为LDA被贝叶斯化了,所以才需要考虑历史先验知识,才加的两个先验参数)。
在pLSA模型中,我们按照如下的步骤得到“文档-词项”的生成模型:
- 按照概率\(P(d_i)\)选择一篇文档\(d_i\)
- 选定文档\(d_i\)后,从主题分布中按照概率\(P(z_k|d_i)\)选择一个隐含的主题类别\(z_k\)
- 选定\(z_k\)后,从词分布中按照概率\(P(w_j|z_k)\)选一个词\(w_j\)
下面,咱们对比下本文开头所述的LDA模型中一篇文档生成的方式是怎样的:
- 按照概率\(P(d_i)\)选择一篇文档\(d_i\)
- 从狄利克雷分布\(\alpha\)中取样生成文档\(d_i\)的主题分布\(\theta_i\)
- 从主题分布\(\theta_i\)中取样生成文档\(d_i\)的第j个主题\(z_{i,j}\)
- 从狄利克雷分布\[\beta\]中取样生成主题对应的词语分布\(\phi_{z_{ij}}\)
- 从词语多项式分布中词语分布\(\phi_{z_{ij}}\)采样生成最终词语\(w_{ij}\)
从上面两个过程可以看出,LDA在PLSA的基础上,为主题分布和词分布分别加了两个Dirichlet先验。
继续拿之前讲解PLSA的例子进行具体说明。如前所述,在PLSA中,选主题和选词都是两个随机的过程,先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后从该主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。

而在LDA中,选主题和选词依然都是两个随机的过程,依然可能是先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后再从该主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。
那PLSA跟LDA的区别在于什么地方呢?区别就在于:
- PLSA中,主题分布和词分布是唯一确定的,能明确的指出主题分布可能就是{教育:0.5,经济:0.3,交通:0.2},词分布可能就是{大学:0.5,老师:0.3,课程:0.2}。
- 但在LDA中,主题分布和词分布不再唯一确定不变,即无法确切给出。例如主题分布可能是{教育:0.5,经济:0.3,交通:0.2},也可能是{教育:0.6,经济:0.2,交通:0.2},到底是哪个我们不再确定(即不知道),因为它是随机的可变化的。但再怎么变化,也依然服从一定的分布,即主题分布跟词分布由Dirichlet先验随机确定。
...来日再来