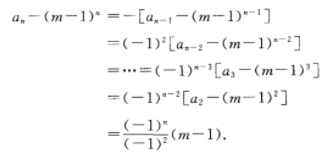算法题
- 大数取TOPK问题 堆:O(nlogk) 快速选择第K大的数,复杂度是O(N)。然后将比它小的全部拿出来,复杂度是O(N)。因此总复杂度是O(2N) = O(N)
- 大数排序问题 分治+K路归并(K路归并可以用堆优化)
机器学习
相关资料
相关题
- 监督学习与无监督学习的区别
- Xgboost与LightGBM
- 判别式模型与生成模型
其它
数学相关
- 中心极限定理:在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布
- 大数定理:在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率
- 大数定律成立条件较宽松。
OSI七层模型
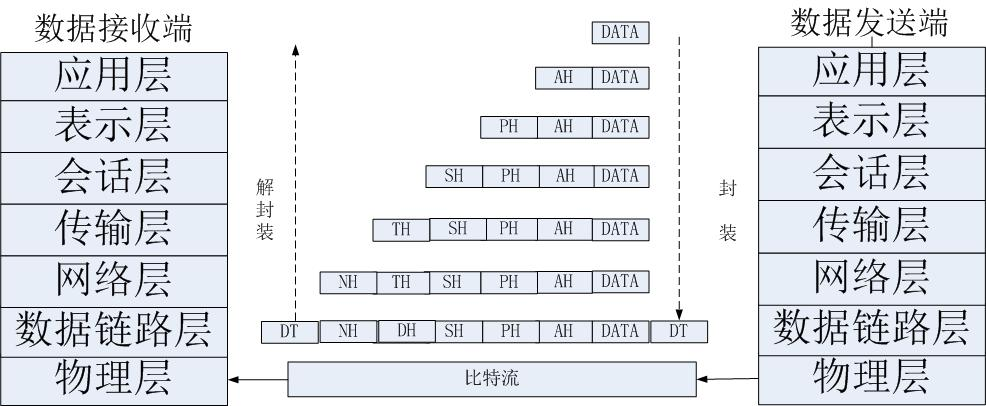

TCP
TCP是TCP/IP体系中一个非常复杂的协议。
- TCP是面向连接的运输层 协议。面向连接的意思是:用之前,必须先建立TCP连接;用完后,必须释放连接。
- TCP连接只能是点对点的。
- TCP提供全双工通信,即允许通信双方在任何时候都能发送数据。(通过发送缓存和接受缓存来实现)
- TCP连接的端点叫:套接字(socket) = (ip地址:端口号)
- 滑动窗口是TCP的精髓:发送方每收到一个确认,就把发送窗口前滑一。
- TCP首部20字节,后面4n字节是内容。
TCP三次握手:
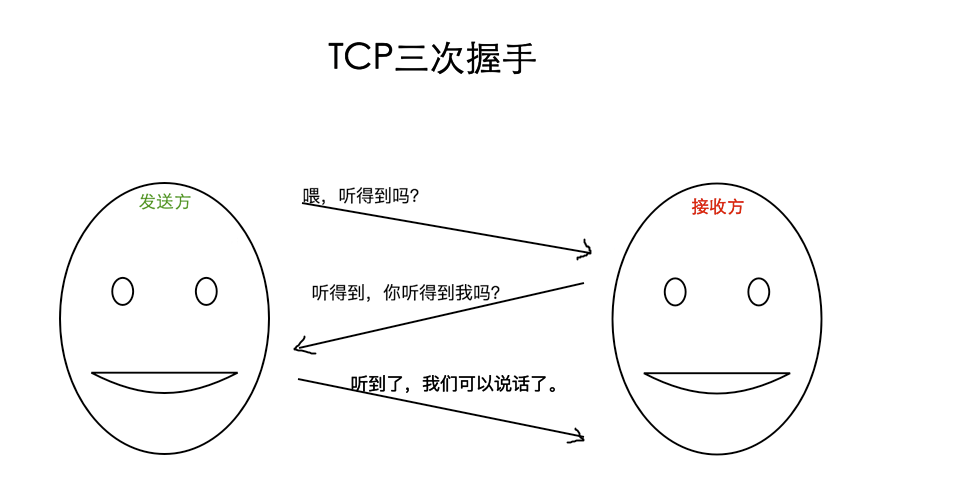
- 第二次对话保证:乙能听懂甲
- 第三次对话保证:甲能听懂乙
TCP四次挥手
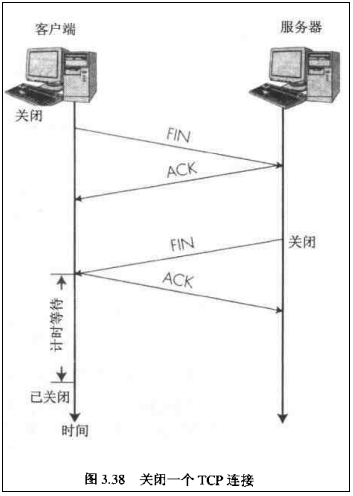
- 第一对FIN和ACK保证了乙知道了要关机;第二对FIN和ACK保证了乙已经关机;
Java内存泄漏
但是在Java中,我们不用(也没办法)自己释放内存,无用的对象由GC自动清理,这也极大的简化了我们的编程工作。但,实际有时候一些不再会被使用的对象,在GC看来不能被释放,就会造成内存泄露。
简单例子:
1 | public class Simple { |
这里的object实例,其实我们期望它只作用于method1()方法中,且其他地方不会再用到它,但是,当method1()方法执行完成后,object对象所分配的内存不会马上被认为是可以被释放的对象,只有在Simple类创建的对象被释放后才会被释放,严格的说,这就是一种内存泄露。解决方法就是将object作为method1()方法中的局部变量。当然,如果一定要这么写,可以改为这样:
1 | public class Simple { |
解决的原则就是尽量减小对象的作用域(比如android studio中,上面的代码就会发出警告,并给出的建议是将类的成员变量改写为方法内的局部变量)以及手动设置null值。




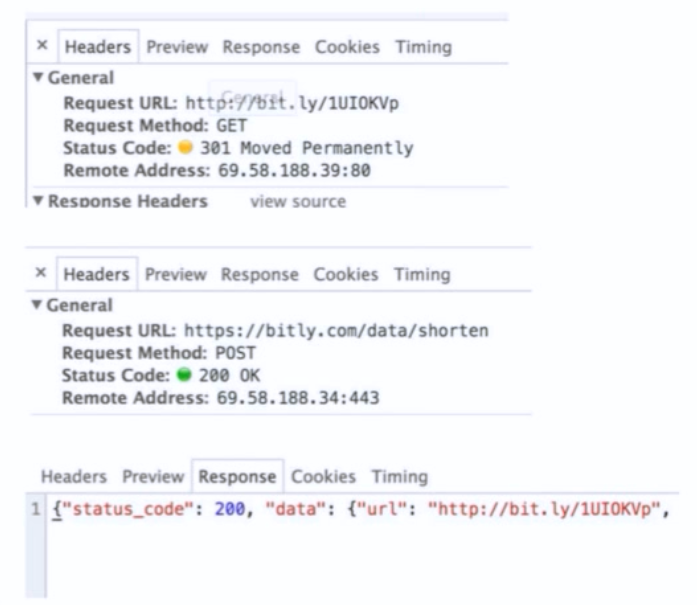
 • 优点:实现简单 • 缺点:生成短网址的长度随着短网址越来越多变得越来越慢 • 可行性:其实能凑合用。在生活中有很多随机编码的,例如机票码、酒店码,是不可重复的,就是用这种方法弄的。
• 优点:实现简单 • 缺点:生成短网址的长度随着短网址越来越多变得越来越慢 • 可行性:其实能凑合用。在生活中有很多随机编码的,例如机票码、酒店码,是不可重复的,就是用这种方法弄的。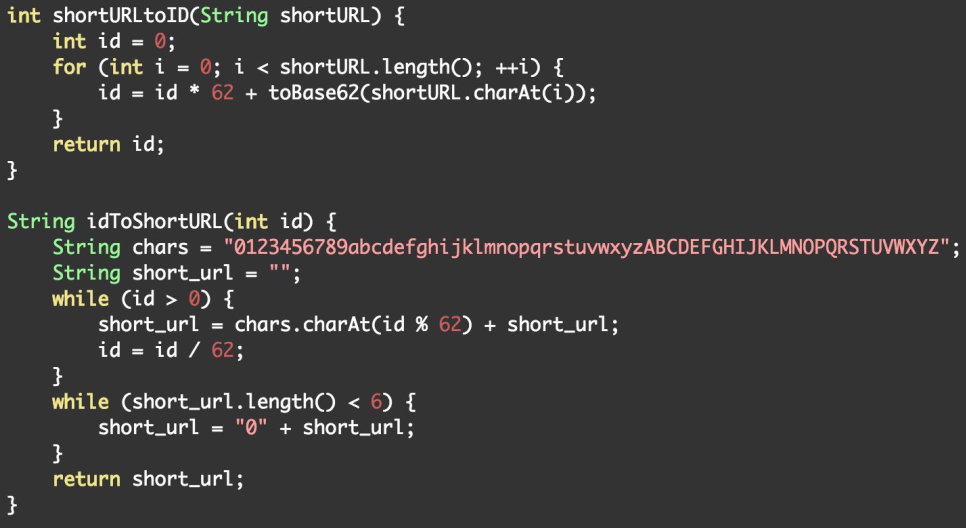
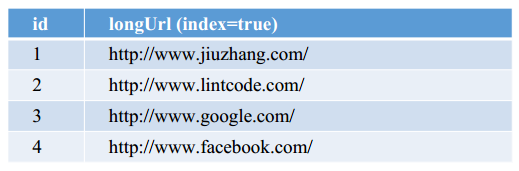
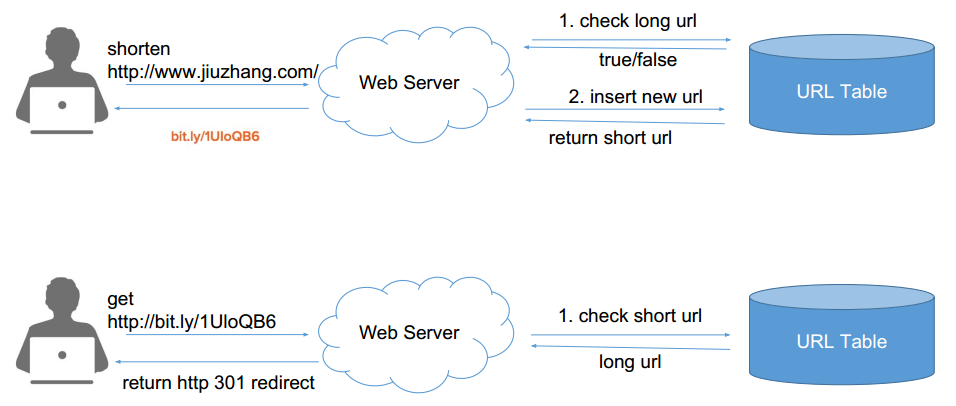 如果选择用 SQL 型数据库,表结构如下:
如果选择用 SQL 型数据库,表结构如下: 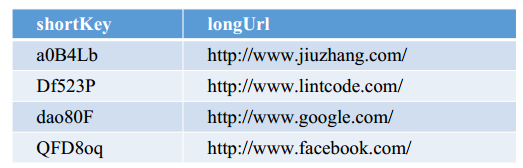 并且需要对shortKey和longURL分别建索引 •
并且需要对shortKey和longURL分别建索引 •