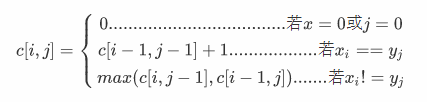甲乙小朋友的房子

甲乙小朋友很笨，但甲乙小朋友不会放弃

0%

发表于 更新于 分类于

理解动态规划

引入例题：triangle

给一个三角形，找到从上到下最短的路径：

1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

最短路径是11 (i.e., 2 + 3 + 5 + 1 = 11).

n = 三角形高度

我们用下面几种方法来思考这个题。

阅读全文 »

发表于 更新于 分类于

首先我们来看一些String的特性。

  • String对象不可变！
  • 在函数的参数传递中，String传进去时是一种拷贝
  • String之间用+号非常不好！（+号内部用的是StringBuilder）
阅读全文 »

发表于 更新于 分类于

LinkedList简介

LinkedList简介

LinkedList 是一个继承于AbstractSequentialList的双向链表。它也可以被当作堆栈、队列或双端队列进行操作。

  • LinkedList 实现 Queue 接口，能对它进行队列操作。

    1
    2
    3
    Queue<Integer> queue = new LinkedList<>();
    queue.offer(1);
    queue.poll();

  • LinkedList 实现 Deque 接口，即能将LinkedList当作双端队列使用。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    Deque<Integer> deque = new LinkedList<>();

    Deque接口的方法：
    // 从头增
    addFirst(element);
    offerFirst(element):如果增加成功，返回true
    push(element);

    // 从尾增
    add(element);
    addLast(element);
    offer(element) ;  如果增加成功，返回true
    offerLast(element); 如果增加成功，返回true

    // 迭代
    iterator();
    descendingIterator();: 逆序迭代

    // 从头删
    pop(element) ; 返回删除的元素
    removeFirst();

    // 从尾删
    removeLast();

    // 需要注意的是
    Collection-->Queue-->Deque--实现-->LinkedList(实现类)
      
    - Deque接口继承了Queue接口,而Queue接口继承了Collection接口,
    - LinkedList实现了Deque接口

    // 一个值得注意的现象：

    LinkedList<Integer> test = new LinkedList<>();
    test.addFirst(1);

    List<Integer> ret = test;
    ret.addFirst(1);// 非法操作！

  • LinkedList 实现了Cloneable接口，即覆盖了函数clone()，能克隆。

  • LinkedList 实现java.io.Serializable接口，这意味着LinkedList支持序列化，能通过序列化去传输。

  • LinkedList 是非同步的。

阅读全文 »

发表于 更新于 分类于

Arrays类中的sort方法可以对对象数组进行排序。但前提是对象所属的类必须实现了Comparable接口。

接口代码

1
2
3
public interface Comparable{
  int compareTo(Object other);
}

为了让某个类实现以上Comparable接口，通常需要以下两个步骤：

  1. 将类声明为实现给定的接口；
  2. 对接口中的所有方法进行定义。
阅读全文 »

发表于 更新于 分类于

Trie树，即字典树/前缀树，又称单词查找树或键树，是一种树形结构。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是最大限度地减少无谓的字符串比较，查询效率比较高。

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

例如有abc,abcd,abd,b,bcd,efg,hii这7个单词，我们构建的树如下所示：

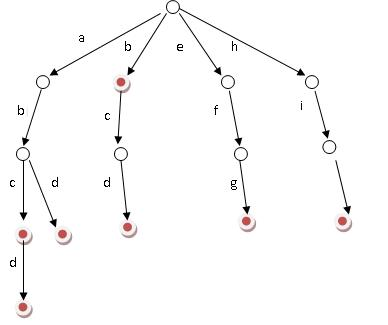
如上图所示，对于每一个节点，从根遍历到他的过程就是一个单词，如果这个节点被标记为红色，就表示这个单词存在，否则不存在。

阅读全文 »

发表于 更新于 分类于

关于动态连通性

我们看一张图来了解一下什么是动态连通性

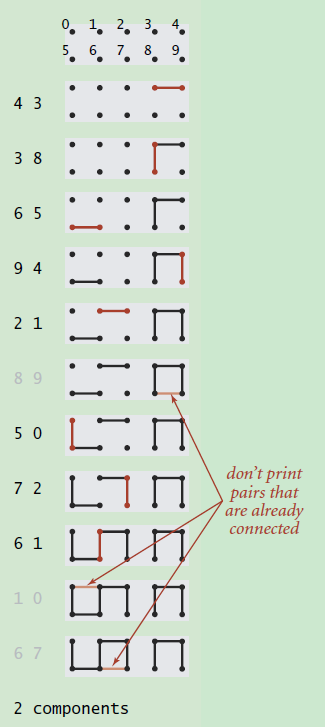
假设我们输入了一组整数对，即上图中的(4, 3) (3, 8)等等，每对整数代表这两个points/sites是连通的。那么随着数据的不断输入，整个图的连通性也会发生变化，从上图中可以很清晰的发现这一点。同时，对于已经处于连通状态的points/sites，直接忽略，比如上图中的(8,9)。

阅读全文 »

发表于 更新于 分类于

子序列：

有序列\(X=<x_1,x_2,...,x_m>\)，另一个子序列\(Z=<z_1,z_2,...,z_k>\)，且Z是按顺序从X中挑出来的。可以跳着挑。

最长公共子序列(LCS)

从两个序列X和Y中，找到最长的公共子序列。

思路

这道题有一个非常巧妙的办法。我们先定义\(c[i,j]表示X_i和Y_j\)的最长公共子序列的长度，那么：

阅读全文 »