本文主要对排序模型做一个简要的整理。首先介绍了一些传统的排序模型,然后介绍比较新的learning to rank.
要想了解L2R,首先我们要了解一下传统的排序模型。
传统的排序模型
传统的排序模型主要分为两类:相关度排序模型和重要性排序模型。
相关度排序模型(Relevance Ranking Model)
相关度排序模型根据查询和文档之间的相似度来对文档进行排序。常用的模型包括:布尔模型(Boolean Model),向量空间模型(Vector Space Model),隐语义分析(Latent Semantic Analysis),BM25,LMIR模型等等。
相关度排序模型主要用在查询(例如搜索引擎)上,它主要是要计算【关键字】与【文档】之间的相关性,给出【关于关键字】的排序。
重要性排序模型(Importance Ranking Model)
重要性排序模型就不考虑上述提到的【查询】,而仅仅根据网页(亦即文档)之间的图结构来判断文档的权威程度,典型的权威网站包括Google,Yahoo!等。常用的模型包括PageRank,HITS,HillTop,TrustRank等等。
传统排序模型的缺陷
以上的这些传统的排序模型,单个模型往往只能考虑某一个方面(相关度或者重要性),所以只是用单个模型达不到要求。搜索引擎通常会组合多种排序模型来进行排序,但是,如何组合多个排序模型来形成一个新的排序模型,以及如何调节这些参数,都是一个很大的问题。
因此,伟大的科学家们提出了Learning to Rank,来解决上述问题。
Learning to Rank
Learning to Rank是一种机器学习模型。它使用机器学习的方法,我们可以把各个现有排序模型的【输出作为特征】,然后训练一个新的模型,并自动学得这个新的模型的参数,从而很方便的可以组合多个现有的排序模型来生成新的排序模型。
L2R特征的选取
与文本分类不同,L2R考虑的是【给定查询的文档集合的排序】。所以,L2R用到的特征不仅仅包含文档d本身的一些特征(比如是否是Spam)等,也包括文档d和给定查询q之间的相关度,以及文档在整个网络上的重要性(比如PageRank值等),亦即我们可以使用相关性排序模型和重要性排序模型的输出来作为L2R的特征。
总结来说,L2R的特征有以下两点:
- 传统排序模型的输出,既包括相关性排序模型的输出f(q,d),也包括重要性排序模型的输出。
- 文档本身的一些特征,比如是否是Spam等。
L2R训练数据的构造
L2R的训练数据可以有三种形式:
- 对于每个查询,各个文档的绝对相关值(非常相关,比较相关,不相关,等等);
- 对于每个查询,两两文档之间的相对相关值(文档1比文档2相关,文档4比文档3相关,等等);
- 对于每个查询,所有文档的按相关度排序的列表(文档1>文档2>文档3)。
这三种形式的训练数据之间可以相互转换,详见[1]。
训练数据的获取有两种主要方法:人工标注[3]和从日志文件中挖掘[4]:
人工标注:首先从搜索引擎的搜索记录中随机抽取一些查询,将这些查询提交给多个不同的搜索引擎,然后选取各个搜索引擎返回结果的前K个,最后由专业人员来对这些文档按照和查询的相关度进行标注。
从日志中挖掘:搜索引擎都有大量的日志记录用户的行为,我们可以从中提取出L2R的训练数据。Joachims提出了一种很有意思的方法[4]:给定一个查询,搜索引擎返回的结果列表为L,用户点击的文档的集合为C,如果一个文档di被点击过,另外一个文档dj没有被点击过,并且dj在结果列表中排在di之前,则di>dj就是一条训练记录。亦即训练数据为:{di>dj|di属于C,dj属于L-C,p(dj) < p(di)},其中p(d)表示文档d在查询结果列表中的位置,越小表示越靠前。
L2R模型训练
L2R是一个有监督学习过程。
对与每个给定的查询-文档对(query document pair),抽取相应的特征(既包括查询和文档之间的各种相关度,也包括文档本身的特征以及重要性等),另外通过或者人工标注或者从日志中挖掘的方法来得到给定查询下文档集合的真实序列。然后我们使用L2R的各种算法来学到一个排序模型,使其输出的文档序列和真实序列尽可能相似。
L2R算法分类和简介
L2R算法主要包括三种类别:PointWise,PairWise,ListWise。
PointWise L2R
pointwise简介 PointWise方法只考虑【给定查询下】,单个文档的绝对相关度,而不考虑其他文档和给定查询的相关度。亦即给定查询q的一个真实文档序列,我们只需要考虑【单个文档di和该查询的相关程度ci】,亦即输入数据应该是如下的形式: 
一种思想是将query与doc之间的相关程度作为标签,比如标签有三档,问题就变为多类分类问题,模型有McRank,svm,最大熵等。另一种思想是将query与doc之间的相关程度作为分数利用回归模型拟合,经典回归模型有线性回归,dnn,mart等。
pointwise形式 输入:doc 的特征向量 输出:每个doc的相关性分数 损失函数: 回归loss,分类loss,有序回归loss
pointwise常用算法 Pointwise方法主要包括以下算法:Pranking (NIPS 2002), OAP-BPM (EMCL 2003), Ranking with Large Margin Principles (NIPS 2002), Constraint Ordinal Regression (ICML 2005)。
pointwise特点 Pointwise方法仅仅使用传统的分类,回归或者Ordinal Regression方法来对给定查询下单个文档的相关度进行建模。这种方法没有考虑到排序的一些特征,比如文档之间的排序结果针对的是给定查询下的文档集合,而Pointwise方法仅仅考虑单个文档的绝对相关度;另外,在排序中,排在最前的几个文档对排序效果的影响非常重要,Pointwise没有考虑这方面的影响。
PairWise
pairwise简介 Pairwise方法考虑给定查询下,【两个文档之间】的相对相关度。亦即给定查询q的一个真实文档序列,我们只需要考虑任意两个相关度不同的文档之间的相对相关度:di>dj,或者di < dj 。
pairwise原理 Pairwise的方法是将文档组成文档对,不单考虑单个文档,而是考虑文档组对是否合理,比如对于query 1返回的三个文档 doc1,doc2,doc3, 有三种组对方式,<doc1,doc2>,<doc2,doc3>,<doc1,doc3>。当三个文档原来的label为3,4,2时,这样组对之后的三个例子就有了新的分数(表达这种顺序是否合理),可以利用这种数据进行分类学习,模型如SVM Rank, 还有RankNet(C. Burges, et al. ICML 2005), FRank(M.Tsai, T.Liu, et al. SIGIR 2007),RankBoost(Y. Freund, et al. JMLR 2003)。
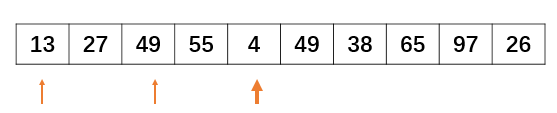
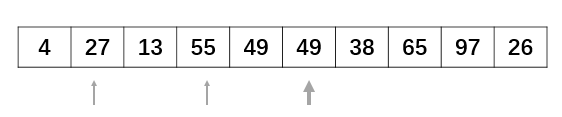
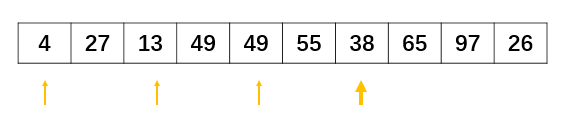
参考文献机器学习排序之Learning to Rank简单介绍对pairwise方法做出了比较容易理解的介绍: 文档对方法(parwise)则将重点转向量对文档顺序关系是否合理进行判断。 之所以被称为文档对方法,是因为这种机器学习方法的训练过程和训练目标,是判断任意两个文档组成的文档对<D0C1,D0C2>是否满足顺序关系,即判断是否D0C1应该排在DOC2的前面。图3展示了一个训练实例:査询Q1对应的搜索结果列表如何转换为文档对的形式,因为从人工标注的相关性得分可以看出,D0C2得分最高,D0C3次之,D0C1得分最低,于是我们可以按照得分大小顺序关系得到3个如图3所示的文档对,将每个文档对的文档转换为特征向量后,就形成了一个具体的训练实例。【备注:根据我的理解,下图有了一些错误。doc1分数应该为3,doc2分数应该为5】。 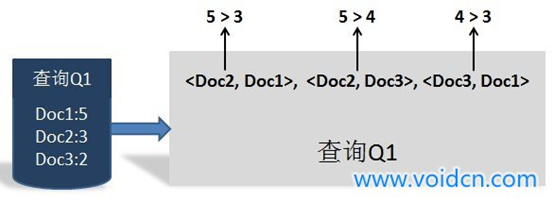 图3 文档对的方法训练实例
图3 文档对的方法训练实例
根据转换后的训练实例,就可以利用机器学习方法进行分类函数的学习,具体的学习方法有很多,比如SVM. Boosts、神经网络等都可以作为具体的学习方法,但是不论具体方法是什么,其学习目标都是一致的,即输入- 个査询和文档对<Docl,DOC2>, 机器学习排序能够判断这种顺序关系是否成立,如果成立,那么在搜索结果中D0C1应该排在D0C2 前面,否则Doe2应该摔在Docl前面,通过这种方式,就完成搜索结果的排序任务。
那么,如何将排序问题转化为机器学习能够学习的分类问题呢?
参考文献Learning to Rank之Ranking SVM 简介给出了一个很好的例子解释这个问题:给定查询q, 文档d1>d2>d3(亦即文档d1比文档d2相关, 文档d2比文档d3相关, x1, x2, x3分别是d1, d2, d3的特征)。为了使用机器学习的方法进行排序,我们将排序转化为一个分类问题。我们定义新的训练样本, 令x1-x2, x1-x3, x2-x3为正样本,令x2-x1, x3-x1, x3-x2为负样本, 然后训练一个二分类器(支持向量机)来对这些新的训练样本进行分类,如下图所示: 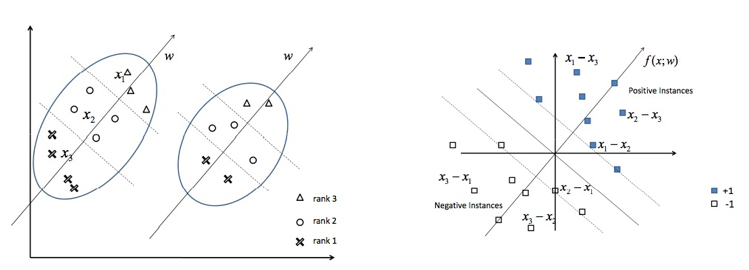 左图中每个椭圆代表一个查询, 椭圆内的点代表那些要计算和该查询的相关度的文档, 三角代表很相关, 圆圈代表一般相关, 叉号代表不相关。我们把左图中的单个的文档转换成右图中的文档对(di, dj), 实心方块代表正样本, 亦即di>dj, 空心方块代表负样本, 亦即di < dj。将【排序问题转化为分类问题】之后, 我们就可以使用常用的机器学习方法解决该问题。
左图中每个椭圆代表一个查询, 椭圆内的点代表那些要计算和该查询的相关度的文档, 三角代表很相关, 圆圈代表一般相关, 叉号代表不相关。我们把左图中的单个的文档转换成右图中的文档对(di, dj), 实心方块代表正样本, 亦即di>dj, 空心方块代表负样本, 亦即di < dj。将【排序问题转化为分类问题】之后, 我们就可以使用常用的机器学习方法解决该问题。
pairwise存在的问题
尽管文档对方法相对单文档方法做出了改进,但是这种方法也存在两个明显的问题:
一个问题是:文档对方法只考虑了两个文档对的相对先后顺序,却没有考虑文档出现在搜索列表中的位置,排在搜索站果前列的文档更为重要,如果前列文档出现判断错误,代价明显高于排在后面的文档。针对这个问题的改进思路是引入代价敏感因素,即每个文档对根据其在列表中的顺序具有不同的权重,越是排在前列的权重越大,即在搜索列表前列如 果排错顺序的话其付出的代价更高?
另外一个问题是:不同的査询,其相关文档数量差异很大,所以转换为文档对之后, 有的查询对能有几百个对应的文档对,而有的查询只有十几个对应的文档对,这对机器学习系统的效果评价造成困难 ?我们设想有两个查询,査询Q1对应500个文文档对,查询Q2 对应10个文档对,假设学习系统对于査询Ql的文档对能够判断正确480个,对于査询 Q2的义格对能够判新正确2个,如果从总的文档对数量来看,这个学习系统的准确率是 (480+2)/(500+10)=0.95.即95%的准确率,但是从査询的角度,两个査询对应的准确率 分别为:96%和20%,两者平均为58%,与纯粹从文档对判断的准确率相差甚远,这对如何继续调优机器学习系统会带来困扰。
ListWise(文档列表方法)
listwise简介 单文档方法将训练集里每一个文档当做一个训练实例,文档对方法将同一个査询的搜索结果里任意两个文档对作为一个训练实例。与Pointwise和Pairwise方法不同,文档列表方法与上述两种表示方式不同,是将每一个查询对应的【所有搜索结果列表整体】作为一个训练实例,这也是为何称之为文档列表方法的原因。
listwise原理 文档列表方法根据K个训练实例(一个査询及其对应的所有搜索结果评分作为一个实 例)训练得到最优评分函数F, 对于一个新的用户査询,函数F 对每一个文档打分,之后按照得分顺序由高到低排序,就是对应的搜索结果。
所以关键问题是:拿到训练数据,如何才能训练得到最优的打分函数?
这里介绍一种训练方法,它是基于搜索结果排列组合的概率分布情况来训练的,图4是这种方式训练过程的图解示意。 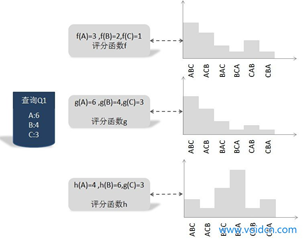 图4 不同评分函数的KL距离
图4 不同评分函数的KL距离
首先解释下什么是搜索结果排列组合的概率分布,我们知道,对于搜索引擎来说,用户输入査询Q, 搜索引擎返回搜索结果,我们假设搜索结果集合包含A、B和C 3个文档,搜索引擎要对搜索结果排序,而这3个文档的顺序共有6种排列组合方式:
ABC, ACB, BAG, BCA, CAB和CBA,
而每种排列组合都是一种可能的搜索结果排序方法。
对于某个评分函数F来说,对3个搜索结果文档的相关性打分,得到3个不同的相关度得分F(A)、F(B)和F(C),根据这3个得分就可以计算6种排列组合情况各自的概率值。
不同的评分函数,其6种搜索结果排列组合的概率分布是不一样的。
了解了什么是搜索结果排列组合的概率分布,我们介绍如何根据训练实例找到最优的评分函数。图4展示了一个具体的训练实例,即査询Q1及其对应的3个文档的得分情况,这个得分是由人工打上去的,所以可以看做是标准答案。
可以设想存在一个最优的评分函数g,对查询Q1来说,其打分结果是:A文档得6分,B文档得4分,C文档得3分,
因为得分是人工打的,所以具体这个函数g是怎样的我们不清楚,我们的任务就是找到一 个函数,使得函数对Ql的搜索结果打分顺序和人工打分顺序尽可能相同。既然人工打分 (虚拟的函数g) 已知,那么我们可以计算函数g对应的搜索结果排列组合概率分布,其具体分布情况如图4中间的概率分布所示。
假设存在两个其他函数h和f,它们的计算方法已知,对应的对3个搜索结果的打分在图上可以看到,由打分结果也可以推出每个函数对应的搜索结果排列组合概率分布,那么h与f哪个与虚拟的最优评分函数g更接近呢?
一般可以用两个分布概率之间的距离远近来度量相似性,KL距离就是一种衡量概率分布差异大小的计算工具,通过分别计算h与g的差异大小及f与g的差异大小,可以看出f比h更接近的最优函数g,那么在这个函数中,我们应该优先选f作为将来搜索可用的评分函数,训练过程就是在可能的函数中寻找最接近虚拟最优函数g的那个函数作为训练结果,将来作为在搜索时的评分函数。
上述例子只是描述了对于单个训练实例如何通过训练找到最优函数,事实上我们有K 个训练实例,虽然如此,其训练过程与上述说明是类似的,可以认为存在一个虚拟的最优 评分函数g(实际上是人工打分),训练过程就是在所有训练实例基础上,探寻所有可能的 候选函数,从中选择那个KL距离最接近于函数g的,以此作为实际使用的评分函数。 经验结果表明,基于文档列表方法的机器学习排序效果要好于前述两种方法。
常用算法 Listwise算法主要包括以下几种算法:LambdaRank (NIPS 2006), AdaRank (SIGIR 2007), SVM-MAP (SIGIR 2007), SoftRank (LR4IR 2007), GPRank (LR4IR 2007), CCA (SIGIR 2007), RankCosine (IP&M 2007), ListNet (ICML 2007), ListMLE (ICML 2008) 。
相比于Pointwise和Pairwise方法,Listwise方法直接优化给定查询下,整个文档集合的序列,所以比较好的解决了克服了以上算法的缺陷。Listwise方法中的LambdaMART(是对RankNet和LambdaRank的改进)在Yahoo Learning to Rank Challenge表现出最好的性能。
参考文献
[1]. Learning to Rank for Information Retrieval. Tie-yan Liu. [2]. Learning to Rank for Information Retrieval and Natural Language Processing. Hang Li. [3]. A Short Introduction to Learning to Rank. Hang Li. [4]. Optimizing Search Engines using Clickthrough Data. Thorsten Joachims. SIGKDD,2002. [5]. Learning to Rank小结








 temp=72
temp=72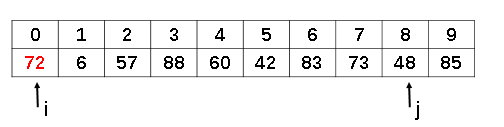
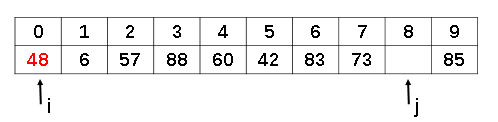
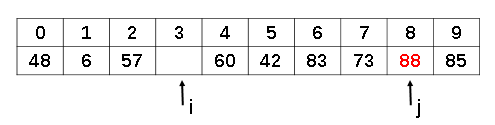
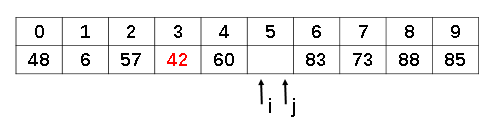

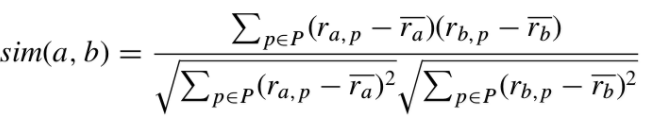 其中: -
其中: - 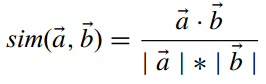 这代表两个user向量的夹角。但这与向量的大小无关,因此伟大的科学家们提出了改进的余弦相似度:
这代表两个user向量的夹角。但这与向量的大小无关,因此伟大的科学家们提出了改进的余弦相似度: 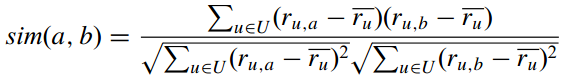 它的取值范围在
它的取值范围在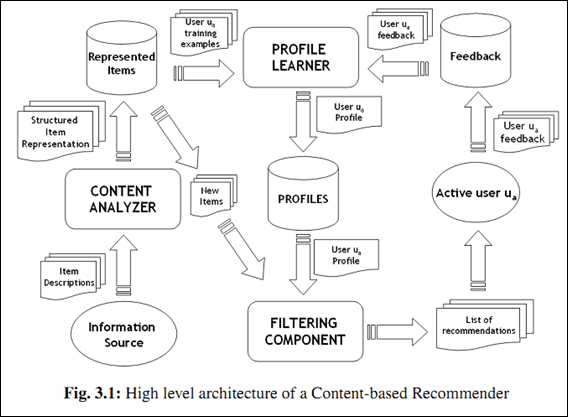 举个例子,对于博客推荐来说,一个item就是一篇博客; - 第一步,首先从文章内容中抽取文章的特征。常用算法就是利用这篇文章的关键词来代表这篇文章,而每个词对应的权重往往使用tf-idf来计算。利用这种方法,将一篇文章用一个向量来表示即可; - 第二步,根据用户过去喜好来刻画用户profile。最简单的方法可以把用户所有喜欢的文章对应的向量的平均值作为此用户的profile。比如某个用户经常关注与推荐系统有关的文章,那么他的profile中“CB”、“CF”和“推荐”对应的权重值就会较高。 - 第三步,利用所有item与用户profile的相关度进行推荐。一个常用的相关度计算方法是向量的cos夹角。最终把候选item里与此用户最相关(cosine值最大)的N个item作为推荐返回给此用户。
举个例子,对于博客推荐来说,一个item就是一篇博客; - 第一步,首先从文章内容中抽取文章的特征。常用算法就是利用这篇文章的关键词来代表这篇文章,而每个词对应的权重往往使用tf-idf来计算。利用这种方法,将一篇文章用一个向量来表示即可; - 第二步,根据用户过去喜好来刻画用户profile。最简单的方法可以把用户所有喜欢的文章对应的向量的平均值作为此用户的profile。比如某个用户经常关注与推荐系统有关的文章,那么他的profile中“CB”、“CF”和“推荐”对应的权重值就会较高。 - 第三步,利用所有item与用户profile的相关度进行推荐。一个常用的相关度计算方法是向量的cos夹角。最终把候选item里与此用户最相关(cosine值最大)的N个item作为推荐返回给此用户。