LU分解条件

如果n阶方阵A的各阶顺序主子式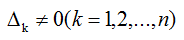，即A的各阶顺序主子矩阵Ak都可逆，则存在唯一的单位下三角矩阵L与唯一的非奇异上三角矩阵U，使得A=LU

其中k阶顺序主子式指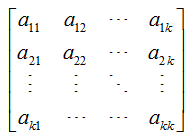

LU分解方法

由于L存在可逆矩阵L'，即LL'=E 则L'A=LL'U=U 因此得出一般的分解方法：通过对(A,E)做初等行变换得到(U,L'),再由L'得到L.

其中：

L是单位下三角矩阵（对角线上的系数都为1的下三角矩阵）；L'也是单位上三角矩阵；
U是非奇异上三角矩阵；

求解方法

对于一般的线性方程组： \[Ax=b\] 如果我们能将A分解成\(A=LU\),即一个下三角阵和一个上三角阵U的乘积，那原方程组的解x便可由下面两步得到：

用前代法解\(Ly=b\)的y；
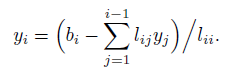
用回代法解\(Ux=y\)的x.

对于列主元消去法，求线性方程组\(Ax=b\)的计算过程可以按照以下步骤进行：

求A的列主元LU分解\(PA=LU\)
解下三角形方程组\(Ly=Pb\)
解上三角形方程组\(Ux=y\)

实现

前代法：需要注意的是，回代法在计算的过程中需要考虑到主元位置序列，并同时对b进行调整。

double * forwardSub(double *lu,int n,double *b,int *p){
    //double *y=new double[n];
    double temp;
      //按qivot对b行变换，与LU匹配
      for(int i=0; i<n-1; i++)  
      {
            temp = b[p[i]];
            b[p[i]] = b[i];
            b[i]=temp;
      }
    for(int i=0; i<n; i++)
            for(int j=0; j<i; j++)
                b[i]=b[i]-lu[n*i+j]*b[j];
    b[n-1]=b[n-1];
    return b;
}

回代法：由于U是上三角矩阵，所以要从x[n-1]开始计算。

double * backSub(double *b,double *lu,int n){
     for(int i=n-1; i>=0; i--)
      {
            for(int j=n-1; j>i; j--)
                b[i]=b[i]-lu[n*i+j]*b[j];
            b[i]=b[i]/lu[n*i+i];
      }
    return b;
}

计算：

bool guass(double *lu,int *p,double*b,int n){
    double * y = forwardSub(lu,n,b,p);
    double * x = backSub(y,lu,n);
    std::cout<<endl<<"the sulution is ; "<<endl;
    for(int i=0;i<n;i++){
        std::cout<<x[i]<<"\t";
    }
    std::cout<<endl;
}

输出：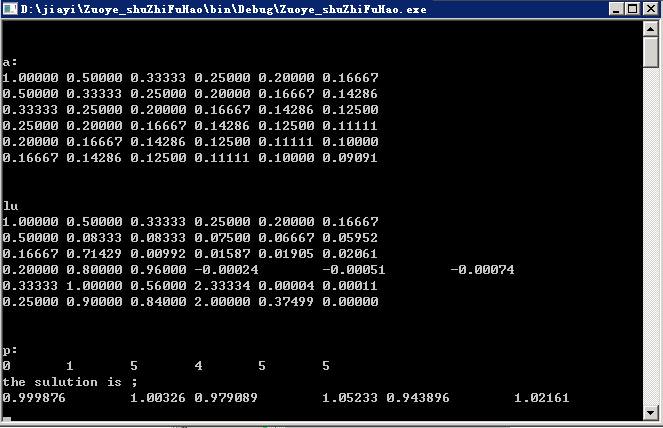

代码：

#include <iostream>
#include<cstdio>
#include<cstdlib>
#include<iomanip>
#define LIM -100000000
using namespace std;
double *luReult;
void printmat(double *mat,int n,string s){
    std::cout<<endl<<endl<<s<<endl;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            printf("%.5f\t",mat[i*n+j]);
        }
        std::cout<<endl;
    }
}
void printarr(int *mat,int n,string s){
    std::cout<<endl<<endl<<s<<endl;
    for(int i=0;i<n;i++){
        std::cout<<mat[i]<<"\t";
        //printf("%s\t",mat[i]);
    }
}
int findMainNumber(double *a,int n,int r){
    float maxa=-99999;
    int maxaIdx=-1;
    //printmat(a,n,"a is now :");
    for(int i=r;i<n;i++){
        if(a[i*n+r]>maxa){
            maxa=a[i*n+r];
            maxaIdx=i;
        }
    }
    return maxaIdx;
}
void exchange(double *a,int n,int e,int r){
    float temp=0;
    for(int i=0;i<n;i++){
        temp = a[r*n+i];
        a[r*n+i]=a[e*n+i];
        a[e*n+i]=temp;
    }
}
bool lu(double* a, int* pivot, int n)//矩阵LU分解
{
      for(int k=0;k<n;k++){
        //寻找第k列的主元
        int p = findMainNumber(a,n,k);
        exchange(a,n,p,k);//交换k行和p行
        pivot[k]=p;//记录置换矩阵p
        if(a[k*n+k]!=0){
                for(int i=k+1;i<n;i++){//部分下三角L
                    a[i*n+k]=a[i*n+k]/a[k*n+k];
                }
                for(int i=k+1;i<n;i++){//计算上三角U
                    for(int j=k+1;j<n;j++){
                        a[i*n+j]=a[i*n+j]-a[i*n+k]*a[k*n+j];
                    }
                }
        }else{
            return true;//矩阵奇异
        }
      }
      /*
      //计算下三角L
      double temp=0;
       for(int i=0; i<n-2; i++)//i行k列
            for(int k=i+1; k<n-1;k++)
            {
                    temp=a[n*pivot[k] + i];
                    a[n*pivot[k] + i]=a[k*n + i];
                    a[k*n + i]=temp;
            }
        */
      luReult=a;
      printmat(a,n,"lu");
      return false ;
}
double radio(int a,int b){
    return (double)(a)/(double)(b);
}
void buildHilbert(double *a,double *b,int n){
    for(int r=0;r<n;r++){
        for(int j=0;j<n;j++){
            a[r*n+j]=radio(1,j+r+1);
            b[r]=b[r]+a[r*n+j];
        }
    }
}
void exchangeb(double *b,int n,int r,int e){
    double temp=0;
    temp=b[e];
    b[e]=b[r];
    b[r]=temp;
    /*r(int i=0;i<n;i++){
        temp=b[r*n+i];
        b[r*n+i]=b[e*n+i];
        b[e*n+i]=temp;
    }*/
}
double * forwardSub(double *lu,int n,double *b,int *p){
    //double *y=new double[n];
    double temp;
      //按qivot对b行变换，与LU匹配
      for(int i=0; i<n-1; i++)
      {
            temp = b[p[i]];
            b[p[i]] = b[i];
            b[i]=temp;
      }
    for(int i=0; i<n; i++)
            for(int j=0; j<i; j++)
                b[i]=b[i]-lu[n*i+j]*b[j];
    b[n-1]=b[n-1];
    return b;
}

double * backSub(double *b,double *lu,int n){
     for(int i=n-1; i>=0; i--)
      {
            for(int j=n-1; j>i; j--)
                b[i]=b[i]-lu[n*i+j]*b[j];
            b[i]=b[i]/lu[n*i+i];
      }
    return b;
}

bool guass(double *lu,int *p,double*b,int n){
    double * y = forwardSub(lu,n,b,p);
    double * x = backSub(y,lu,n);
    std::cout<<endl<<"the sulution is ; "<<endl;
    for(int i=0;i<n;i++){
        std::cout<<x[i]<<"\t";
    }
    std::cout<<endl;
}
int main()
{
    int n=6;//矩阵是n*n的
    double *b=new double[n];
    double *a=new double[n*n];
    /*double input[n*n]={0.001,1.00,1.00,2.00};
    a=input;
    double inputb[n]={1.00,3.00};
    b=inputb;*/
    buildHilbert(a,b,n);
    printmat(a,n,"a:");
    int *pivot=new int[n*n];
    luReult=new double[n*n];
    lu(a,pivot,n);
    printarr(pivot,n,"p:");
     guass(luReult,pivot,b,n);
    //cout << "Hello world!" << endl;
    return 0;
}

甲乙小朋友的房子

求线代方程的解

LU分解条件

LU分解方法

求解方法

实现