感觉自己还是太渣,看了些许算法,并不知道有什么卵用。决定好好分析分析别人的思路,也许能够对我带来些许启发。
本文主要针对天池大数据竞赛之“O2O优惠券使用预测”的冠军队伍的思路和源码分析。在此感谢无私的前辈(诗人都藏在水底)[https://github.com/wepe/O2O-Coupon-Usage-Forecast]。
本文主要对数据的抽取extract_feature.py做一些详细的分析。
解决方案概述
本赛题提供了用户线下消费和优惠券领取核销行为的纪录表,用户线上点击/消费和优惠券领取核销行为的纪录表,记录的时间区间是2016.01.01至2016.06.30,需要预测的是2016年7月份用户领取优惠劵后是否核销。根据这两份数据表,我们首先对数据集进行划分,然后提取了用户相关的特征、商家相关的特征,优惠劵相关的特征,用户与商家之间的交互特征,以及利用本赛题的leakage得到的其它特征(这部分特征在实际业务中是不可能获取到的)。最后训练了XGBoost,GBDT,RandomForest进行模型融合。
源码分析
第二赛季暂时没有平台,所以本文只对第一赛季的源码进行分析。
文件:O2O-Coupon-Usage-Forecast/code/wepon/season one
这个文件夹存放第一赛季的代码 - extract_feature.py划分数据集,提取特征,生成训练集(dataset1和dataset2)和预测集(dataset3)。 - xgb.py 训练xgboost模型,生成特征重要性文件,生成预测结果。单模型第一赛季A榜AUC得分0.798.
import概述
分析对象:extract_feature.py
import包概述
1
2
3
| import pandas as pd
import numpy as np
from datetime import date
|
pandas
Pandas 是基于 NumPy (因此还要import numpy) 的一个非常好用的库,正如名字一样,人见人爱。之所以如此,就在于不论是读取、处理数据,用它都非常简单。Pandas提供了很多处理大数据的方法。我想是因为此,原作者才采用了它。
Pandas 有两种自己独有的基本数据结构。Series 和 DataFrame,它们让数据操作更简单了。
两种结构的属性和方法不再多阐述。见两份很好的参考文档:
- Pandas 使用
- 十分钟搞定pandas
- 在Python中利用Pandas库处理大数据的简单介绍
- pandas官方文档
- pandas常见方法,中文
大概知道了import包的内容后,我们正式开始看源码。
注意
- 读取之前,请先把数据的表头项删除(也就是第一行的string)
读取数据集
总结:
| 1 |
ccf_offline_stage1_train |
用户线下消费和优惠券领取行为 |
off_train |
| 2 |
ccf_online_stage1_train |
用户线上点击/消费和优惠券领取行为 |
on_train |
| 3 |
offline_stage1_test_revised |
用户O2O线下优惠券使用预测样本 |
off_test |
源码分析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
off_train = pd.read_csv('data/ccf_offline_stage1_train.csv',header=None)
off_train.columns = ['user_id','merchant_id','coupon_id','discount_rate','distance','date_received','date']
off_test = pd.read_csv('data/ccf_offline_stage1_test_revised.csv',header=None,nrows=3000)
off_test.columns = ['user_id','merchant_id','coupon_id','discount_rate','distance','date_received']
on_train = pd.read_csv('data/ccf_online_stage1_train.csv',header=None,nrows=47000)
on_train.columns = ['user_id','merchant_id','action','coupon_id','discount_rate','date_received','date']
|
读数据主要用了pandas的read_cvs方法. 为了快捷分析,我们限定只读取数据集的前7w、3k、47w行
采集特征
主要特征
总结:
| dataset3 |
table3,off_test |
off_test数据 |
| dataset2 |
table2,off_train |
领券时期在20160515-20160615之间的 |
| dataset1 |
table2,off_train |
领券日期在20160414-20160514的 |
| feature3 |
table2,off_train |
消费data在20160315-20160630的,或领券日期在20160315-20160630但没有消费的 |
| feature2 |
table2,off_train |
消费日期在20160201-20160514的,或领券日期在20160201-20160514但没有消费的 |
| feature1 |
table2,off_train |
消费日期在20160101-20160413的,或领券日期在20160101-20160413但没有消费的 |
这是滑窗的方法得到多份训练数据集,特征区间越小,得到的训练数据集越多。划分方式:
|
领券了的 |
消费了的+领券了没消费的 |
| 测试集 |
dataset3 |
feature3 |
| 训练集1 |
dataset2 |
feature2 |
| 训练集2 |
dataset1 |
feature1 |
上面这个表格很清晰地说明了原作者划分数据的方法.
源码分析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
dataset3 = off_test
feature3 = off_train[
((off_train.date>='20160315')&(off_train.date<='20160630'))
|((off_train.date=='null')&(off_train.date_received>='20160315')&(off_train.date_received<='20160630'))]
dataset2 = off_train[
(off_train.date_received>='20160515')&off_train.date_received<='20160615')]
feature2 = off_train[(off_train.date>='20160201')&(off_train.date<='20160514')|((off_train.date=='null')&(off_train.date_received>='20160201')&(off_train.date_received<='20160514'))]
dataset1 = off_train[(off_train.date_received>='20160414')&(off_train.date_received<='20160514')]
feature1 = off_train[(off_train.date>='20160101')&(off_train.date<='20160413')|((off_train.date=='null')&(off_train.date_received>='20160101')&(off_train.date_received<='20160413'))]
|
其他特征
other_feature3
| t |
每个用户使用优惠券的总次数 |
| t1 |
每个用户使用不同优惠券的次数 |
| t2 |
每个用户使用某张优惠券(使用次数大于1次)的首次和末次使用时间 |
| t3 |
每个用户用优惠券date;本优惠券首、末次间隔;本优惠券首/末次使用date |
| t4 |
每个用户每天使用优惠券的次数 |
| t5 |
每个用户每天使用每张优惠券的次数 |
| t6 |
用户使用每张优惠券的date,不同date用冒号分隔 |
| t7 |
用户使用每张券的时间,以及和前、后一张券的时间间隔 |
文件名:data/other_feature3.csv
格式:user_id,coupon_id,this_month_user_receive_same_coupon_count,this_month_user_receive_all_coupon_count,date_received,this_month_user_receive_same_coupon_lastone,this_month_user_receive_same_coupon_firstone,this_day_user_receive_all_coupon_count,this_day_user_receive_same_coupon_count,day_gap_before,day_gap_after
解释:用户id,优惠券id,本月用户使用本券次数,本月用户使用所有券次数,使用时间,本月用户使用本券末次时间、首次时间,本日用户用券总数,本日用户用本券总数,上次用本券间隔,下次用本券间隔
源码分析
t:计算每个用户使用优惠券的总次数:
1
2
3
4
5
6
7
|
t = dataset3[['user_id']]
t['this_month_user_receive_all_coupon_count'] = 1
t = t.groupby('user_id').agg('sum').reset_index()
|
t1:统计每个用户,使用不同优惠券的次数:
1
2
3
4
5
| t1 = dataset3[['user_id','coupon_id']]
t1['this_month_user_receive_same_coupon_count'] = 1
t1 = t1.groupby(['user_id','coupon_id']).agg('sum').reset_index()
|
t2:找出每个人,消费每个券的时间,并用冒号分隔例如:
1
2
3
4
5
| t2 = dataset3[['user_id','coupon_id','date_received']]
t2.date_received = t2.date_received.astype('str')
t2 = t2.groupby(['user_id','coupon_id'])['date_received'].agg(lambda x:':'.join(x)).reset_index()
|
t2:每个用户使用某张优惠券(使用次数大于1次)的首次和末次使用时间
1
2
3
4
5
6
7
8
9
10
|
t2['receive_number'] = t2.date_received.apply(lambda s:len(s.split(':')))
t2 = t2[t2.receive_number>1]
t2['max_date_received'] = t2.date_received.apply(lambda s:max([int(d) for d in s.split(':')]))
t2['min_date_received'] = t2.date_received.apply(lambda s:min([int(d) for d in s.split(':')]))
t2 = t2[['user_id','coupon_id','max_date_received','min_date_received']]
|
t3:每个用户使用优惠券的时间、本次优惠券与首次使用的间隔、末次使用的间隔
1
2
3
4
5
6
7
8
9
10
11
12
13
| t3 = dataset3[['user_id','coupon_id','date_received']]
t3 = pd.merge(t3,t2,on=['user_id','coupon_id'],how='left')
t3 = t3.apply(pd.to_numeric, args=('coerce',))
t3['this_month_user_receive_same_coupon_lastone'] = t3.max_date_received - t3.date_received
t3['this_month_user_receive_same_coupon_firstone'] = t3.date_received - t3.min_date_received
|
上面跑到t3['this_month_user_receive_same_coupon_lastone'] = t3.max_date_received - t3.date_received的时候会出现TypeError: unsupported operand type(s) for -: 'float' and 'str'.
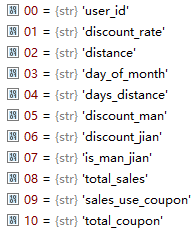
在执行这句话之前,我们看到t3.date_received的类型为
因此我们需要将数据类型先转换为float。在网上查到本方法对本代码有效(暂不知原因)。参考文献
t3 = t3.apply(pd.anumeric, args=('coerce',))
把这句话加上后,我们看到
定义函数is_firstlastone判断优惠券是否是末次使用
1
2
3
4
5
6
7
| def is_firstlastone(x):
if x==0:
return 1
elif x>0:
return 0
else:
return -1
|
t3:加上两个数据,...
1
2
3
| t3.this_month_user_receive_same_coupon_lastone = t3.this_month_user_receive_same_coupon_lastone.apply(is_firstlastone)
t3.this_month_user_receive_same_coupon_firstone = t3.this_month_user_receive_same_coupon_firstone.apply(is_firstlastone)
t3 = t3[['user_id','coupon_id','date_received','this_month_user_receive_same_coupon_lastone','this_month_user_receive_same_coupon_firstone']]
|
后面套路差不多,此处不再继续分析。主要结论已经总结在上表中。 # 合并特征
生成训练集
coupon2 = pd.read_csv('data/coupon2_feature.csv')
merchant2 = pd.read_csv('data/merchant2_feature.csv')
user2 = pd.read_csv('data/user2_feature.csv')
user_merchant2 = pd.read_csv('data/user_merchant2.csv')
other_feature2 = pd.read_csv('data/other_feature2.csv')
#dataset2是根据 优惠券特征 合并商户、用户、用户-商户、其他特征
dataset2 = pd.merge(coupon2,merchant2,on='merchant_id',how='left')
dataset2 = pd.merge(dataset2,user2,on='user_id',how='left')
dataset2 = pd.merge(dataset2,user_merchant2,on=['user_id','merchant_id'],how='left')
dataset2 = pd.merge(dataset2,other_feature2,on=['user_id','coupon_id','date_received'],how='left')
dataset2.drop_duplicates(inplace=True)
print dataset2.shape
dataset2.user_merchant_buy_total = dataset2.user_merchant_buy_total.replace(np.nan,0)
dataset2.user_merchant_any = dataset2.user_merchant_any.replace(np.nan,0)
dataset2.user_merchant_received = dataset2.user_merchant_received.replace(np.nan,0)
dataset2['is_weekend'] = dataset2.day_of_week.apply(lambda x:1 if x in (6,7) else 0)
weekday_dummies = pd.get_dummies(dataset2.day_of_week)
weekday_dummies.columns = ['weekday'+str(i+1) for i in range(weekday_dummies.shape[1])]
dataset2 = pd.concat([dataset2,weekday_dummies],axis=1)
dataset2['label'] = dataset2.date.astype('str') + ':' + dataset2.date_received.astype('str')
dataset2.label = dataset2.label.apply(get_label)
dataset2.drop(['merchant_id','day_of_week','date','date_received','coupon_id','coupon_count'],axis=1,inplace=True)
dataset2 = dataset2.replace('null',np.nan)
dataset2.to_csv('data/dataset2.csv',index=None)
coupon1 = pd.read_csv('data/coupon1_feature.csv')
merchant1 = pd.read_csv('data/merchant1_feature.csv')
user1 = pd.read_csv('data/user1_feature.csv')
user_merchant1 = pd.read_csv('data/user_merchant1.csv')
other_feature1 = pd.read_csv('data/other_feature1.csv')
dataset1 = pd.merge(coupon1,merchant1,on='merchant_id',how='left')
dataset1 = pd.merge(dataset1,user1,on='user_id',how='left')
dataset1 = pd.merge(dataset1,user_merchant1,on=['user_id','merchant_id'],how='left')
dataset1 = pd.merge(dataset1,other_feature1,on=['user_id','coupon_id','date_received'],how='left')
dataset1.drop_duplicates(inplace=True)
print dataset1.shape
dataset1.user_merchant_buy_total = dataset1.user_merchant_buy_total.replace(np.nan,0)
dataset1.user_merchant_any = dataset1.user_merchant_any.replace(np.nan,0)
dataset1.user_merchant_received = dataset1.user_merchant_received.replace(np.nan,0)
dataset1['is_weekend'] = dataset1.day_of_week.apply(lambda x:1 if x in (6,7) else 0)
weekday_dummies = pd.get_dummies(dataset1.day_of_week)
weekday_dummies.columns = ['weekday'+str(i+1) for i in range(weekday_dummies.shape[1])]
dataset1 = pd.concat([dataset1,weekday_dummies],axis=1)
dataset1['label'] = dataset1.date.astype('str') + ':' + dataset1.date_received.astype('str')
dataset1.label = dataset1.label.apply(get_label)
dataset1.drop(['merchant_id','day_of_week','date','date_received','coupon_id','coupon_count'],axis=1,inplace=True)
dataset1 = dataset1.replace('null',np.nan)
dataset1.to_csv('data/dataset1.csv',index=None)
生成预测集
coupon3 = pd.read_csv('data/coupon3_feature.csv')
merchant3 = pd.read_csv('data/merchant3_feature.csv')
user3 = pd.read_csv('data/user3_feature.csv')
user_merchant3 = pd.read_csv('data/user_merchant3.csv')
other_feature3 = pd.read_csv('data/other_feature3.csv')
dataset3 = pd.merge(coupon3,merchant3,on='merchant_id',how='left')
dataset3 = pd.merge(dataset3,user3,on='user_id',how='left')
dataset3 = pd.merge(dataset3,user_merchant3,on=['user_id','merchant_id'],how='left')
dataset3 = pd.merge(dataset3,other_feature3,on=['user_id','coupon_id','date_received'],how='left')
dataset3.drop_duplicates(inplace=True)
print dataset3.shape
dataset3.user_merchant_buy_total = dataset3.user_merchant_buy_total.replace(np.nan,0)
dataset3.user_merchant_any = dataset3.user_merchant_any.replace(np.nan,0)
dataset3.user_merchant_received = dataset3.user_merchant_received.replace(np.nan,0)
dataset3['is_weekend'] = dataset3.day_of_week.apply(lambda x:1 if x in (6,7) else 0)
weekday_dummies = pd.get_dummies(dataset3.day_of_week)
weekday_dummies.columns = ['weekday'+str(i+1) for i in range(weekday_dummies.shape[1])]
dataset3 = pd.concat([dataset3,weekday_dummies],axis=1)
dataset3.drop(['merchant_id','day_of_week','coupon_count'],axis=1,inplace=True)
dataset3 = dataset3.replace('null',np.nan)
dataset3.to_csv('data/dataset3.csv',index=None)
附录
查看dataFrame类型的内容
见pandas 文档之 10 minutes to pandas --- viewing data
用t.values,t.columns
lambda functions
源代码中有一行t2.groupby(['user_id','coupon_id'])['date_received'].agg(lambda x:':'.join(x)).reset_index()
官方文档
lambda functions是python的一个function. 用例:
#函数f(x)
>>> def f(x):
... return x*2
...
>>> f(3) #输入x=3
6 #输出6
#f(x)等价于:
>>> g = lambda x: x*2 1
>>> g(3)
6
#f(x)还等价于:
>>> (lambda x: x*2)(3) 2
6
作者代码中,有一行
lambda x:':'.join(x)即将前后叠加,用:连接 t2.groupby(['user_id','coupon_id'])['date_received'].agg(lambda x:':'.join(x)).reset_index()意思是将数据集先按照user_id','coupon_id排序,然后对date_received进行用:连接一起来
例如,输入:
1
2
3
4
5
6
| df = pd.DataFrame({'A' : ['foo', 'bar', 'foo', 'bar',
'foo', 'bar', 'foo', 'foo'],
'B' : ['one', 'one', 'two', 'three',
'two', 'two', 'one', 'three'],
'C' : np.random.randn(8),
'D' : np.random.randn(8)})
|
| 0 |
foo |
one |
0.754147 |
0.912176 |
| 1 |
bar |
one |
1.414635 |
-0.760638 |
| 2 |
foo |
two |
-0.142930 |
-1.290766 |
| 3 |
bar |
three |
1.196999 |
1.647513 |
| 4 |
foo |
two |
-0.261663 |
1.284779 |
| 5 |
bar |
two |
1.622070 |
1.685648 |
| 6 |
foo |
one |
1.478855 |
-0.229636 |
df3 = df.groupby(['A'])['B'].agg(lambda x:':'.join(x)).reset_index()
输出:
| 0 |
bar |
one:three:two |
| 1 |
foo |
one:two:two:one:three |
pandas的merge的how参数
原代码出现了t3 = pd.merge(t3,t2,on=['user_id','coupon_id'],how='left')
how参数主要决定了哪一个keys会被包含在结果表中。它的值有四种可能性:left,right,outer,inner。我们主要看left和right
how='left':遍历left表,找与right一样的,依次放入行。 如果没有,则设为NAN


因此t3 = pd.merge(t3,t2,on=['user_id','coupon_id'],how='left')的意思是:
根据t3合并t2的user_id','coupon_id


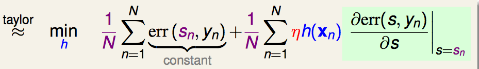
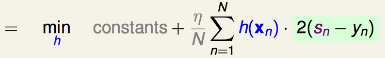
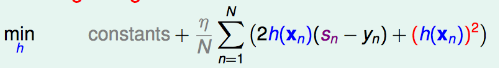



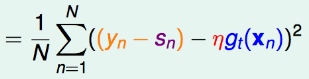







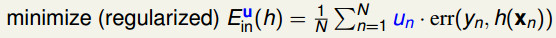


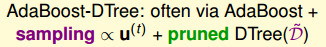


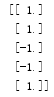

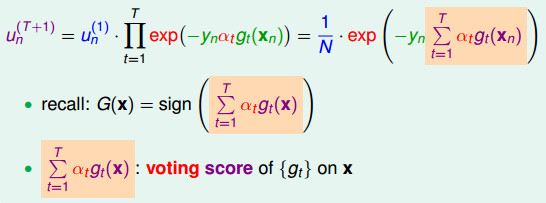
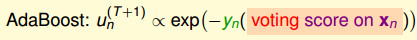



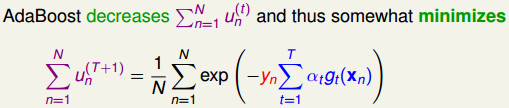

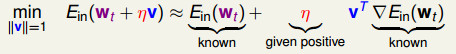
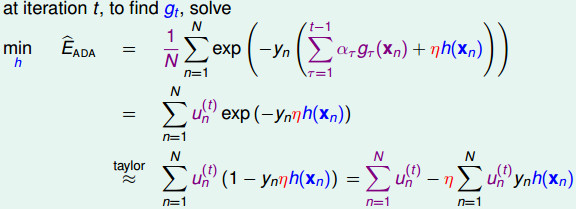
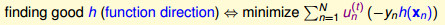

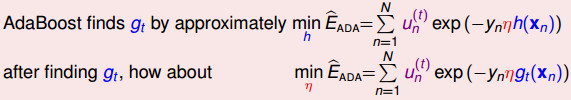

 ,我们得到最佳的
,我们得到最佳的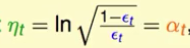
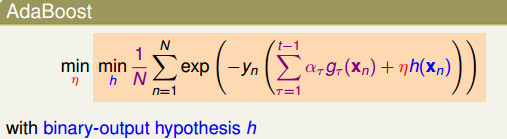
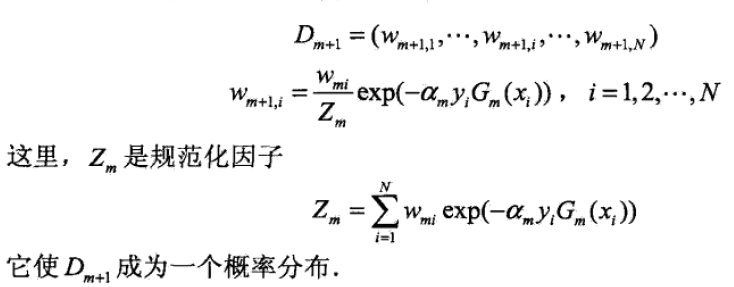 5. 将上面迭代k次后,得到M个基本分类器。构建基本分类器的线性组合:
5. 将上面迭代k次后,得到M个基本分类器。构建基本分类器的线性组合: 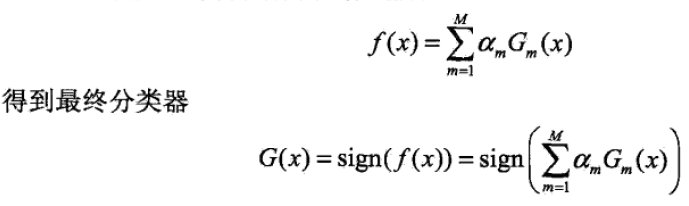


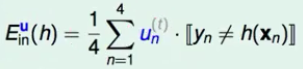
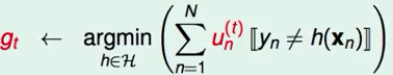
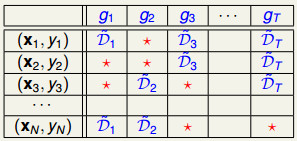
 -- 表现不好的定义: --- 将
-- 表现不好的定义: --- 将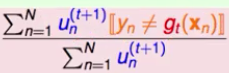 --- 为了简便,定义橙色方块为所有犯错误的
--- 为了简便,定义橙色方块为所有犯错误的 -- 表现不好的选择方法: --- 将本次正确的
-- 表现不好的选择方法: --- 将本次正确的
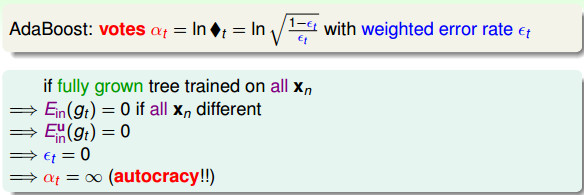
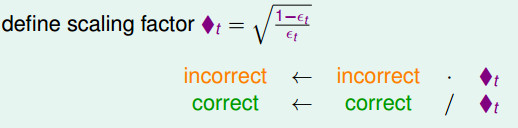 - ◆t有更清晰的物理意义,通常情况下εt < 1/2(因为是学习之后的结果,错误率应该小于0.5), - ◆t将大于1; - 那么,犯错的数据将乘上大于1的数,正确数据将除以大于1的数 - 使得提升了犯错数据的权重(scale up incorrect), - 降低做对数据的权重(scale down correct) - 这样使得更加专注在犯了错的地方,来得到不一样的假设(diverse hypotheses)。
- ◆t有更清晰的物理意义,通常情况下εt < 1/2(因为是学习之后的结果,错误率应该小于0.5), - ◆t将大于1; - 那么,犯错的数据将乘上大于1的数,正确数据将除以大于1的数 - 使得提升了犯错数据的权重(scale up incorrect), - 降低做对数据的权重(scale down correct) - 这样使得更加专注在犯了错的地方,来得到不一样的假设(diverse hypotheses)。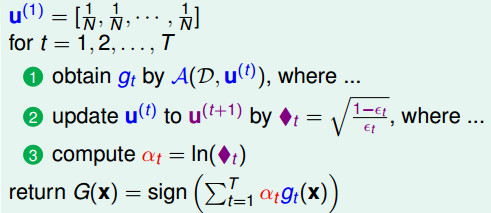


 AdaBoost的保证是让一个很弱的算法不断变强,最终得到一个很强是算法(Ein=0,Eout is small)。
AdaBoost的保证是让一个很弱的算法不断变强,最终得到一个很强是算法(Ein=0,Eout is small)。  # Adaptive Boosting的实际应用表现 上面的AdaBoost只需要一个很弱的算法就可以使用。 一般情况下,可以使用决策桩(Decision Stump),该模型相当于在某一个维度上的Perceptron模型。
# Adaptive Boosting的实际应用表现 上面的AdaBoost只需要一个很弱的算法就可以使用。 一般情况下,可以使用决策桩(Decision Stump),该模型相当于在某一个维度上的Perceptron模型。 

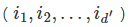

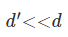


 在实际应用中,面对非线性的问题时,可以通过随机森林的方法来进行初步的特征选择。
在实际应用中,面对非线性的问题时,可以通过随机森林的方法来进行初步的特征选择。