甲乙小朋友的房子

甲乙小朋友很笨，但甲乙小朋友不会放弃

0%

发表于 更新于 分类于

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

阅读全文 »

发表于 更新于 分类于

大纲

  • 有序数组
    • Merge两个有序数组
      • 将小数组归并到大数组里
      • 两个数组的交集
      • 数组点乘
  • 子数组
    • 前缀和
  • Two Sum
    • Hash Map vs Two pointers
  • Two Pointers
阅读全文 »

发表于 更新于 分类于 ，

本文主要参考自吴恩达Coursera深度学习课程 DeepLearning.ai 编程作业（1-4）

吴恩达Coursera课程 DeepLearning.ai 编程作业系列，本文为《神经网络与深度学习》部分的第四周“深层神经网络”的课程作业。

本节的主要内容是：利用之前实现的神经网络，来识别图片中的猫

阅读全文 »

发表于 更新于 分类于 ，

本文主要参考自吴恩达Coursera深度学习课程 DeepLearning.ai 编程作业（1-4）

吴恩达Coursera课程 DeepLearning.ai 编程作业系列，本文为《神经网络与深度学习》部分的第四周“深层神经网络”的课程作业。

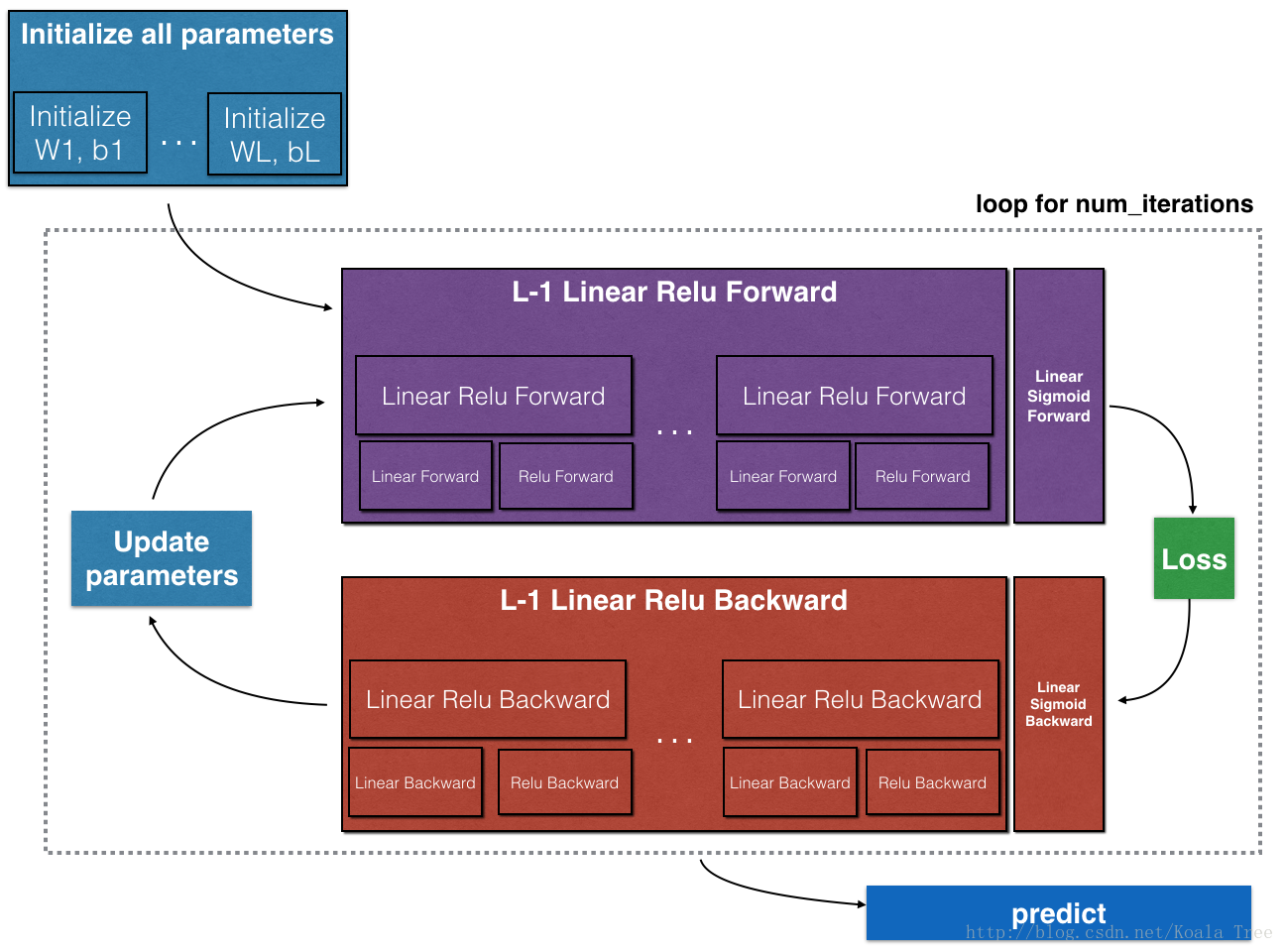
本节的主要内容是：实现L层的神经网络

大纲

首先完成一些helper function。然后再建立两层、多层神经网络：

  • 两层和多层神经网络的初始化
  • 实现前向传播模型
    • 实现某一层的前向传播 - 输出\(Z^{[l]}\)
    • 激活层已给出
    • 将前两步结合
    • 将前向传播迭代L-1次，然后将激活层加到最后，就完成了L层的前向传播
  • 计算误差
  • 实现后向传播模型
    • 实现某一层的后向传播
    • 激活层的后向传播已给出
    • 将前两步结合
    • 将后向传播迭代L-1次，然后将激活层加到最后，完成了L层的后向传播
  • 更新参数

阅读全文 »

发表于 更新于 分类于

链表

链表考点

  • 会不会写程序 - 类、指针、引用等

知识点

  • 链表中的Dummy Node
  • 基本链表技能
  • 链表的Two Pointers(Fast-slow pointers)

入门题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void print(){
  for(ListNode node = head; node != null; node = node.next){
    System.out.print(node.val);
    System.out.print("->");
  }
  System.out.println("null");
}

void main(){
  ListNode node1 = new ListNode(1);
  ListNode node2 = new ListNode(2);
  ListNode node3 = new ListNode(3);
  
  ListNode head = node1;
  
  node1.next = node2;
  node2.next = node3;
  
  print(head); // 输出啥？
  
  node1 = node2;
  
  print(head); // 输出啥？
}

答案：

1
2
3
1->2->3->null

1->2->3->null

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
初始：

  n1      n2        n3
[1,-]--> [2,-]--> [3,null]
===================================
head = n1 : 

 head
  n1      n2        n3
[1,-]--> [2,-]--> [3,null]

sizeof(head) = 4 
===================================
n1 = n2 : 

 head     n1
          n2        n3
[1,-]--> [2,-]--> [3,null]
阅读全文 »

发表于 更新于 分类于

一些题目 implement of ....

时间复杂度训练

复习：

\[T(n) = T(\frac{n}{2}) + O(1) → O(logn)\]

\[T(n) = T(\frac{n}{2}) + O(n) → O(n)\]

** 问题1**

通过O(1)的时间,把n的问题,变为了两个n/2的问题,复杂度是多少?

\[T(n) = 2T(\frac{n}{2}) + O(1) → O(n)\]

解决：树型分析法

1
2
3
4
5
6
7
8
9
           n
       /      \      -->  本次拆分耗费了O(1)的时间
     n/2       n/2
    / \        / \   -->  本次拆分耗费了O(2)的时间
n/4   n/4   n/4   n/4
.....................
         第k+1层       -->  本次拆分耗费了O(2^k)的时间
.....................  -->  本次拆分耗费了O(n/2)的时间

总复杂度：

\[O(1+2+4+....+2^k+...+\frac{n}{2})\tag{1}\]

设\(2^m = \frac{n}{2}\)，则\(m=log(\frac{n}{2})=logn-log2=logn\)

则公式（1）等于：

\[O(2^0+2^1+2^2+....+2^{logn})\]

\[=O(\frac{a_1(1-q^n)}{1-q})=O(\frac{1-2^{logn}}{2-1})=O(n)\tag{结果}\]

阅读全文 »

发表于 更新于 分类于

# 二分查找

给一个已排序的数组，找到target的位置（第一个出现的、最后一个出现的、任意的）位置。如果没有target，返回-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
target = 5

    start                    end
      ↓                       ↓
index 0  1  2  3  4  5  6  7  8
nums  2  3  5  8 13 21 34 55 89
      
======================================

mid = [start + end ] / 2 = 8/2 = 4
  
    start        mid         end
      ↓           ↓           ↓
index 0  1  2  3  4  5  6  7  8
nums  2  3  5  8 13 21 34 55 89
  
nums[mid] > target  -> target一定在左边 --> end = mid

======================================

mid = [start + end ] / 2 = 4/2 = 2
  
    start  mid   end
      ↓     ↓     ↓
index 0  1  2  3  4  5  6  7  8
nums  2  3  5  8 13 21 34 55 89
  
nums[mid] == target  ->  got it ! 
  
复杂度分析

T(n) = T(n/2) + O(1)

解得 T(n) = O(logn)
阅读全文 »